同态加密技术总结
同态加密技术总结
同态加密的概念
同态加密(Homomorphic Encryption)是很久以前密码学界就提出来的一个问题。早在1978年,Ron Rivest, Leonard Adleman, 以及Michael L. Dertouzos就以银行为应用背景提出了这个概念。其中Ron Rivest和Leonard Adleman分别就是著名的RSA算法中的R和A。
同态加密是基于数学难题的计算复杂性理论的密码学技术。对经过同态加密的数据进行处理得到一个输出,将这一输出进行解密,其结果与用同一方法处理未加密的原始数据得到的输出结果是一样的。
第一个构造出全同态加密(Fully Homomorphic Encryption)的Craig Gentry给出的直观定义是:
A way to delegate processing of your data, without giving away access to it.
一种不需要访问数据本身就可以加工数据的方法
同态加密的具体过程
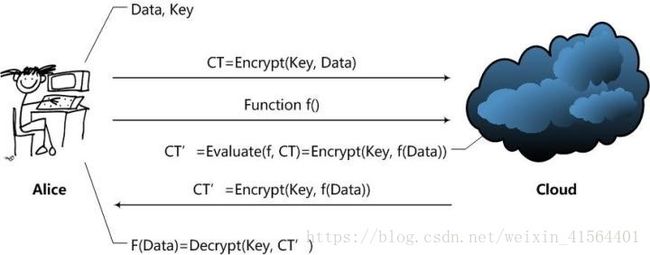
以云计算应用场景为例,如图1所示。Alice通过Cloud,以Homomorphic Encryption(以下简称HE)处理数据的整个处理过程大致是这样的:
- Alice对数据进行加密。并把加密后的数据发送给Cloud;
- Alice向Cloud提交数据的处理方法,这里用函数f来表示;
- Cloud在函数f下对数据进行处理,并且将处理后的结果发送给Alice;
- Alice对数据进行解密,得到结果。
据此,我们可以很直观的得到一个HE方案应该拥有的函数:
- KeyGen函数:密钥生成函数。这个函数应该由Alice运行,用于产生加密数据Data所用的密钥Key。同时应该还有一些公开常数PP(Public Parameter);
- Encrypt函数:加密函数。这个函数也应该由Alice运行,用Key对用户数据Data进行加密,得到密文CT(Ciphertext);
- Evaluate函数:评估函数。这个函数由Cloud运行,在用户给定的数据处理方法f下,对密文进行操作,使得结果相当于用户用密钥Key对f(Data)进行加密。
- Decrypt函数:解密函数。这个函数由Alice运行,用于得到Cloud处理的结果f(Data)。
根据f的限制条件不同,HE方案实际上分为了两类:
- Fully Homomorphic Encryption (FHE):这意味着HE方案支持任意给定的f函数,只要这个f函数可以通过算法描述,用计算机实现。显然,FHE方案是一个非常棒的方案,但是计算开销极大,暂时还无法在实际中使用。
- Somewhat Homomorphic Encryption (SWHE):这意味着HE方案只支持一些特定的f函数。SWHE方案稍弱,但也意味着开销会变得较小,容易实现,现在已经可以在实际中使用。
同态加密的安全性
HE方案的最基本安全性是语义安全性(Semantic Security)。直观地说,就是密文(Ciphertext)不泄露明文(Plaintext)中的任意信息。如果用公式表述的话,为:
![]() (1)
(1)
这里PK代表公钥(Public Key),公式中的"约等于"符号,意味着多项式不可区分性,即不存在高效的算法,可以区分两个结果,即使已知m0, m1和PK。这是因为加密算法中还用到一个很重要的量:随机数。也就是说,对于同样的明文m进行加密,得到的结果都不一样,即一个明文可以对应多个密文(many ciphertexts per plaintext)。
在密码学中,还有更强的安全性定义,叫做选择密文安全性(Chosen Ciphertext Security)。选择密文安全性分为非适应性(None-Adaptively)和适应性(Adaptively),也就是CCA1和CCA2。HE方案是不可能做到CCA2安全的。那么,HE方案能不能做到CCA1安全呢?至今还没有CCA1安全的FHE方案,但是在2010年,密码学家们就已经构造出了CCA1的SWHE方案了。
HE方案还有一方面的安全性,就是函数f是否也可以保密?如果能保密,Cloud不仅不能够得到数据本身的内容,现在连数据怎么处理的都不知道,只能按照给定的算法执行,然后返回的结果就是用户想要的结果。如果HE方案满足这样的条件,我们称这个HE方案具有Function-Privacy特性。不过,现在还没有Function-privacy FHE,甚至Function-privacy SWHE也没有。
部分同态加密的例子
在2009年Graig Gentry给出FHE的构造前,很多加密方案都具有部分同态的性质。实际上,最经典的RSA加密,其本身对于乘法运算就具有同态性。Elgamal加密方案同样对乘法具有同态性。Paillier在1999年提出的加密方案也具有同态性,而且是可证明安全的加密方案。2009年前的HE方案要不只具有加同态性,要不只具有乘同态性,但是不能同时具有加同态和乘同态。这种同态性用处就不大了,只能作为一个性质,这类方案的同态性一般也不会在实际中使用的。
以Elgamal加密方案为例,其具有乘同态性, Elgamal加密方案的密文形式为:
![]() (2)
(2)
其中r是加密过程中选的一个随机数,g是一个生成元,h是公钥。如果我们有两个密文:
![]() (3)
(3)
我们把这两个密文的第一部分相乘,第二部分相乘,会得到:
![]() (4)
(4)
也就是说,相乘以后的密文正好是m1m2所对应的密文。这样,用户解密后得到的就是m1m2的结果了。而且注意,整个运算过程只涉及到密文和公钥,运算过程不需要知道m1m2的确切值。所以我们说Elgamal具有乘同态性质。但是很遗憾,其没有加同态性质。
同态加密的实现与效率
FHE最重要的一点是Fully,就是说要支持任意的函数f。因此我们也可以很明显看出,想要构造FHE,就需要了解计算机是如何计算的。一般来说,我们有两种思路:
- 从计算机原理考虑。计算机无论做何种运算,归根到底都是位运算。实际上,一个计算机只要支持逻辑与运算(AND),以及异或运算(XOR),那么这个计算机理论上就可以实现计算机的其他运算了(我们称之为图灵完备性,Turing Completeness)
- 从抽象代数考虑。我们只需要加法和乘法就可以完成全部运算了。但其实更严格的说,只要我们在一个域(Field)上构造HE,理论上我们就可以支持所有的f。
2011年Gentry和Halevi在IBM尝试实现了两个HE方案:Smart-Vercauteren的SWHE方案以及Gentry的FHE方案,并公布了效率。Smart-Vercauteren的SWHE方案效率如图2所示。

图2. Smart-Vercauteren方案(SWHE)的效率
Smart-Vercauteren的方案的密钥时间还能接受,但这个是部分同态加密。Gentry的FHE方案的效率如图3所示。
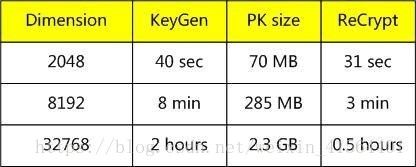
图3. Gentry的FHE方案的效率
Halevi在github上公布了同态加密库HElib(https://github.com/shaih/HElib.git)的代码,其中实现了完全同态加密的加、减、乘、除、移位、循环移位等功能,目前的问题在于上述生成密钥的效率上。如果计算的量大于生成秘钥所需的时间量的话,是有价值使用HElib库的。
同态加密的应用
同态加密技术在分布式计算环境下的密文数据计算方面具有比较广泛的应用领域,比如云计算、多方保密计算、匿名投票等
6.1安全云计算与委托计算
同态技术在该方面的应用可以使得我们在云环境下,充分利用云服务器的计算能力,实现对明文信息的运算,而不会有损私有数据的私密性。例如医疗机构通常拥有比较弱的数据处理能力,而需要第三方来实现数据处理分析以达到更好的医疗效果或者科研水平,这样他们就需要委托有较强数据处理能力的第三方实现数据处理(云计算中心),但是医院负有保护患者隐私的义务,不能直接将数据交给第三方。在同态加密技术的支持下,医疗机构就可以将加密后的数据发送至第三方,待第三方处理完成后便可返回给医疗结构。整个数据处理过程、数据内容对第三方是完全透明的。
6.2文件存储与密文检索
用户可以将自己的数据加密后存储在一个不信任的远程服务器上,日后可以向远程服务器查询自己所需要的信息,存储与查询都使用密文数据,服务器将检索到的密文数据发回。用户可以解密得到自己需要的信息,而远程服务器却对存储和检索的信息一无所知。此种方法同样适用于搜索引擎的数据检索。
6.3安全多方计算协议设计的工具
所谓安全多方计算就是分别持有私有数据 x1,x2,…,xn的 n 个人,在分布式环境中协同计算函数f (x1,x2,…,xn) 而不泄露各方的私有数据。以同态技术加密的密文数据计算不仅可以满足安全多方计算协议设计中保护各方隐私的需要,还能避开不经意传输协议而大大提升协议效率。
6.4电子选举
基于同态加密技术设计的电子选举方案,统计方可以在不知道投票者投票内容的前提下,对投票结果进行统计,既保证了投票者的隐私安全,有能够保证投票结果的公证。
写在最后
同态加密技术目前的实用难度在于效率,不能达到一定效率的同台加密实用性并不高,但是这一技术在效率提升之后有着广阔的应用前景!
本文资料收集于网络,由笔者进行整理。