前几天听了 CMU 一大神的算法公开课,算是近距离见识了算法大神的冰山一角,管中窥豹,可见一斑。
先稍微介绍一下大神,方便感兴趣的童鞋进一步了解他。
- 姓名:王赟 Maigo
- Maigo 的知乎专栏
- Maigo 的 Github
想了解更多的就自己谷歌吧。知乎专栏就够看好久的了。
我写这篇文字的目的很简单,
- 分享给需要的和感兴趣的同学
- 看了好几遍视频,还是想自己从头到尾复述一遍以加深印象,熟悉 bit 的操作。
算法的所有代码,java 版本和 swift 版本,我都放在了我的 Github 上。当然还有欢迎订阅我的博客。
为了找工作过 OA 关,也是没办法用 swift,更不想用 C++,还不如临时学 java 来的效率点。所以这里就用 java 代码来讲解一下。我这里用的是 “15 queens”,共5个方法,第四个开始速度有了质的提升,但需要第三个方法的基础,反正后一个的提升都基于前一个。
Queen 1
我自己的电脑上跑的时间是// Time elapsed: 28423ms。用的是最基础的回溯法(back tracking)。最后就不把所有的解都打印出来了,打印的时间其实和算法本身关系并不大,而且因为是15 皇后,容易死机。
public class Main {
private static final int n = 15;
private static int count = 0;
private static int[] sol;
public static void main(String[] args) {
sol = new int[n];
long tic = System.currentTimeMillis();
DFS(0);
long toc = System.currentTimeMillis();
System.out.println("Total solutions: " + count);
System.out.println("Time elapsed: " + (toc - tic) + "ms");
}
private static void DFS(int row) {
for (int col = 0; col < n; col++) {
boolean ok = true;
// 注意下面这个循环,后面会做改进
for (int i = 0; i < row; i++) {
if (col == sol[i] || i - row == sol[i] - col || i - row == col - sol[i]) {
ok = false;
break;
}
}
if (!ok) continue;
sol[row] = col;
if (row == n - 1) {
count++;
} else {
DFS(row + 1);
}
}
}
}
Queen 2
Queen1 的时间是:// Time elapsed: 28423ms
这个方法的时间是:// Time elapsed: 16024ms
这里就需要开始介绍一个小窍门,因为上面的方法,每次都要和之前的所有行相比较(看上面代码的注释部分),如果我们可以用一个 boolean 数组,记录下每一列,每一个对角线的情况,就可以不用所有都比较了。那么如何求行和列呢
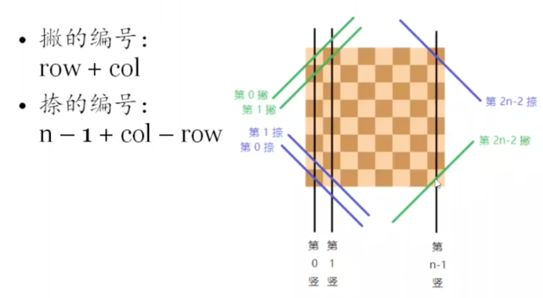
如上图,一共有 2n - 1 个对角线,大神是语言研究所的博士生,他用的是中文的“竖”,“撇”和“捺”来表示两种对角线,可以很容易知道它们的 index 就是 0 -> 2n - 2。所以上面的代码注释部分就可以改成:
int j = col + row, k = n - 1 + col - row;
if (shu[col] || pie[j] || na[k]) continue;
就是如果当前列和对角线都被占用的话,就直接 continue。当然我们还需要设置和清除。把已经被占用的设为 true,一趟完事了就重新设为 false。
shu[col] = true; pie[j] = true; na[k] = true;
DFS(row + 1);
shu[col] = false; pie[j] = false; na[k] = false;
Queen 3
Queen1 :// Time elapsed: 28423ms
Queen2 :// Time elapsed: 16024ms
这个方法:// Time elapsed: 10302ms
从这个方法开始引入 bit array,关键点是:
用 32 位的 bit array(也就是一个整数(int)的长度),代替 32 位长度的 boolean 。
位运算的基本操作是:与,或,异或,取反,左移,右移。很容易理解,这里瞬间就节省了超多的空间。也很容易就想到这里并不会节省时间很多时间,因为整个的流程是没什么太大的区别的。所以上面的 boolean[] shu, pie, na; 就成了 int shu, pie, na;,默认为 0。上面的判断条件也成了
if ((((shu >> col) | (pie >> (col + row)) | (na >> (n - 1 + col - row))) & 1) != 0) continue;
这个乍一看有点复杂,先看一下这个 bit 是如何模拟数组操作的,其实就是读和写:
- 写
把第 i 位置1:a |= (1 << i)
把第 i 位置0: a &= ~(1 << i)
把第 i 位取反:a ^= (1 << i)
- 读
读取第 i 位的值:(a >> i)&1
所以上面那个条件其实就是取第col位的值 (shu >> col) & 1,每个都是这样,所以就先把三个都|或起来,再和 1 &与。操作是等价的,存储空间不同而已。后面的设置与清除也成了:
shu ^= (1 << col); pie ^= (1 << (row + col)); na ^= (1 << (n - 1 + col - row));
就是把shu的第col位置1,本来是0,取反就成了1。用异或的好处就是清除和设置的代码相同,更方便。
Queen 4
Queen1 :// Time elapsed: 28423ms
Queen2 :// Time elapsed: 16024ms
Queen3 :// Time elapsed: 10302ms
这个方法:// Time elapsed: 1962ms
可以从上面这个时间比较看出来瞬间少了个数位。因为这一方法用到了系统级别的运算,利用了 bit array 可以一步操作多位的优势,不像一般的 array,必须要一个一个操作,而 bit array 可以在一个整形的长度内,O(1) 时间任意存取任意位置的数。为了更好的理解这个方法,这里我们需要介绍另一个 bit 的操作,取最后一个 1:
a & -a
懂负数的原理就很容易理解了,负数就是取反+1。例子:
a = 0001100
-a = 1110011 + 1 = 1110100
a & -a = 0000100
枚举 bit array 中的1,就是:
while(a != 0) {
int p = a & -a; // p 就是取出来的 1
a ^= p;
Do something with p;
}
之前是枚举每个位置,然后检查是否冲突,而现在我们可以利用这点,直接枚举不冲突的位置。那么在第 row 行,相应的shu,pie,na中冲突的位置在哪里呢?
shu 冲突的位置:shu
pie 冲突的位置:pie >> row
na 冲突的位置:na >> (n - 1 - row)
就是之前式子 pie[row + col], na[n - 1 + col - row] 的一个变形,用 bit array 来代替普通的 boolean array。所以现在这个 DFS 方法就成了:
private static void DFS(int row) {
int ok = ((1 << n) - 1) & ~(shu | (pie >> row) | (na >> (n - 1 - row)));
while (ok != 0) {
int p = ok & -ok;
ok ^= p;
if (row == n - 1) {
count++;
} else {
shu ^= p; pie ^= (p << row); na ^= (p << (n - 1 - row));
DFS(row + 1);
shu ^= p; pie ^= (p << row); na ^= (p << (n - 1 - row));
}
}
}
Queen 5
Queen1 :// Time elapsed: 28423ms
Queen2 :// Time elapsed: 16024ms
Queen3 :// Time elapsed: 10302ms
Queen4 :// Time elapsed: 1962ms
这个方法:// Time elapsed: 1350ms
为了更好的理解这个方法,这里有个 google developer 的文档,讲的是 Propagation and backtracking。所谓的 Propagation,就是:
Propagation consists of taking some constraint—which might be a constraint of the original problem, or a constraint learned or hypothesized along the way—and applying it to variables.
利用之前学到的,来限制接下来的。
这个方法中,我们把 shu,pie,na 都当成形参,把当前行学到的“不能放”的限制信息,保留到下一行,从而限制下一行的决策。这也就是 Propagation 的意思。所以我们的代码也就成了
public class Main {
private static final int n = 15;
private static int count = 0;
public static void main(String[] args) {
long tic = System.currentTimeMillis();
DFS(0, 0, 0, 0);
long toc = System.currentTimeMillis();
System.out.println("Total solutions: " + count);
System.out.println("Time elapsed: " + (toc - tic) + "ms");
}
private static void DFS(int row, int shu, int pie, int na) {
// shu, pie, na 当前行的位置不能放
int ok = ((1 << n) - 1) & ~(shu | pie | na);
while (ok != 0) {
int p = ok & -ok;
ok ^= p;
if (row == n - 1) {
count++;
} else {
// 把当前行的 shu,pie,na 设为 0,从而之后的所有行都不能放
DFS(row + 1, shu ^ p, (pie ^ p) >> 1, (na ^ p) << 1);
}
}
}
}