用matlab编写SIR模型对SARS期间疫情数据进行模拟
SIR模型是传染病研究当中的一个重要模型,SIR由Susceptible(易感人但未感染节点)、Infective(感染节点)和Removal(移出节点)三种基本的节点模型组成,除了S/I/R参数之外,还引入两个重要的参数,感染强度β,和恢复强度γ,分别表示传染病的传染性和患者的治愈能力。经典SIR模型的数学表达式如下:

本质上这是一个常微分方程,我们可以使用matlab中的ode方法对这个方程进行数值解的计算,我们根据ode的规则编写函数把这个微分方程的数学语言翻译成matlab语言如下:
function dP = SIR_model(t,P) %t是时间,P中含有模型的五个参数SIRβγ
beta = P(4)
gama = P(5)
dP = zeros(5,1);
dP(1) = -beta*P(1)*P(2);
dP(2) = beta*P(1)*P(2) - gama*P(2);
dP(3) = gama*P(2);
end
徐宝春[1]在其硕士论文中对参数进行了估计,我们引用他的数据可以编写以下程序模拟,与真实数据进行对比并且做出图形:
%确定参数
I0=497
R0=33
%估计参数
S0=1290
beta=8e-5
gama=4e-2
[t,P] = ode45(@SIR_model,[1:1:70],[S0 I0 R0 beta gama]);
S = P(:,1); %Susceptible 未感染者;未感染节点;
I = P(:,2);%Infective 感染者;感染节点;
R = P(:,3); %Removal 移出者(死亡或者治愈并且免疫者);移出节点;
figure(1)
plotnum = 70
subplot(2,1,1)
realI =[530,685,708,734,761,800,840,883,928,970,998,1059,1108,1150,1190,1232,1268,1297,1327,1358,1380,1402,1434,1458,1488,1510,1527,1543,1557,1572,1589,1600,1611,1621,1629,1637,1646,1654,1661,1667,1674,1678,1683,1689,1698,1703,1706,1710,1713,1714,1718,1719,1722,1724,1724,1725,1726,1728,1730,1732,1736,1739,1742,1746,1747,1748,1748,1750,1752,1752,1753,1754,1755];
prealI = get_head_elements(realI,plotnum)
num = 1:plotnum
plot(num,prealI,'-x');
title('SARS期间累计个案趋势图')
xlabel('时间(以3月31日为第一天)')
ylabel('累计个案数')
subplot(2,1,2);
RI=R+I
plot(t,RI,'-ro')
title('SIR模型预估SARS期间累计个案趋势图')
xlabel('时间(以3月31日为第一天)')
ylabel('累计个案数')
figure(2)
plot(num,prealI,'-x');
hold on;
plot(t,RI,'-ro')
legend('真实数据','模拟数据','location','southeast')
title('SARS期间累计个案趋势图')
xlabel('时间(以3月31日为第一天)')
ylabel('累计个案数')
##############2020年6月25日更#################
注意我们这里使用了自己编写的get_head_elements函数,用来获取数据最前面的len位。
function head = get_head_elements(colVect,len)
for i =1:len
head(i)=colVect(i);
end
header = head';
end
##############2020年6月25日更#################
运行之后我们可以得到以下图形:
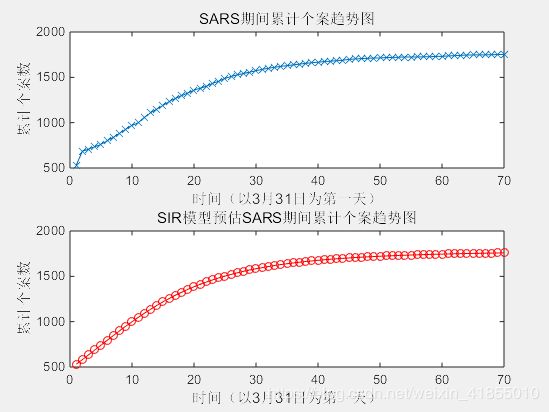

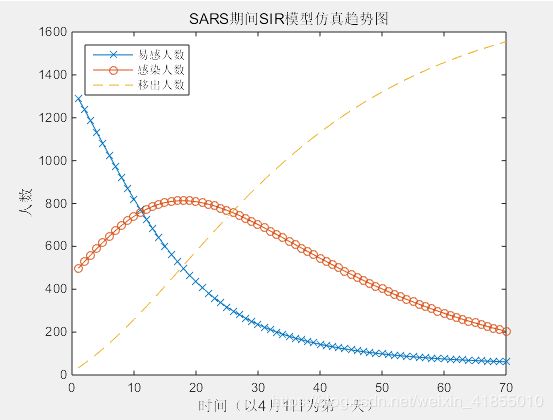
可以看出这个模型从后验的角度可以很好的描述整个疫情。
参考文献:
[1]徐宝春,基于SIR模型的SARS传染病研究,[D]山东大学,2019