Python金融大数据分析——第11章 统计学（1）正态性检验 笔记

第11章 统计学

11.1 正态性检验

可以说 ， 正态分布是金融学中最重要的分布 ， 也是金融理论的主要统计学基础之一。尤其是下面这些金融理论基础 ， 在很大程度上依赖于股票市场收益的正态分布。

投资组合理论
当股票收益呈正态分布时，最优化投资组合可以在这样的环境中选择： 只有平均收益和收益的方差（或者波动率）以及不同股票之间的协方差与投资决策（即最优化投资组合构成）相关。

资本性资产定价模型
同样． 当股票收益呈正态分布时 ， 单独证券的价格可以很好地以和某种大规模市场指数的关系表示：这种关系通常用单一股票与市场指数的联动指标（ β β ）表示。

有效市场假设
有效市场指的是价格反映所有可用信息的市场 ， 其中的 “所有”可以是挟义的 ，也可以是广义的（例如 “所有公开信息”或者同时包括 “只为个人所有 ” 的信息）；如果这个假设成立 ， 股票价格波动将是随机的，而收益呈正态分布。

期权定价理论
布朗运动是随机股票（和其他证券）价格变动的标准、 基准模型：著名的 Black-Scholes-Merton 期权定价公式使用几何布朗运动作为股票在一段时间内随机波动的模型，这种波动造成收益呈正态分布。

上述的理论只是支持金融学中正态性假设重要性的一部分原因。

11.1.1 基准案例

几何布朗运动中的路径特性：

正态对数收益率
在两点之间的对数收益率 logStSs=logSt−logSs(0<s<t) l o g S t S s = l o g S t − l o g S s ( 0 < s < t )

对数-正太价值
在任何时点 t>0 , 价值 S_t 呈正态分布

import numpy as np
import scipy.stats as scs
import statsmodels.api as sm
import matplotlib as mpl
import matplotlib.pyplot as plt

np.random.seed(1000)


# 为几何布朗运动生成蒙特卡洛路径
def gen_paths(S0, r, sigma, T, M, I):
    """
    Generates Monte Carlo paths for geometric Brownian motion.
    :param S0: initial stock/index value
    :param r: constant short rate
    :param sigma: constant volatility
    :param T: final time horizon
    :param M: number of time steps/intervals
    :param I: number of paths to be simulated
    :return:ndarray,shape(M+1,I)
    simulated paths given the parameters
    """
    dt = float(T) / M
    paths = np.zeros((M + 1, I), np.float64)
    paths[0] = S0
    for t in range(1, M + 1):
        rand = np.random.standard_normal(I)
        rand = (rand - rand.meand()) / rand.std()
        paths[t] = paths[t - 1] * np.exp((r - 0.5 * sigma ** 2) * dt + sigma * np.sqrt(dt) * rand)
    return paths

下面是蒙特卡洛模拟的一种可能的参数化， 和 gen_paths 函数相结合， 生成25万条路径，每条有 50 个时间步：

S0 = 100.
r = 0.05
sigma = 0.2
T = 1.0
M = 50
I = 250000
paths = gen_paths(S0, r, sigma, T, M, I)

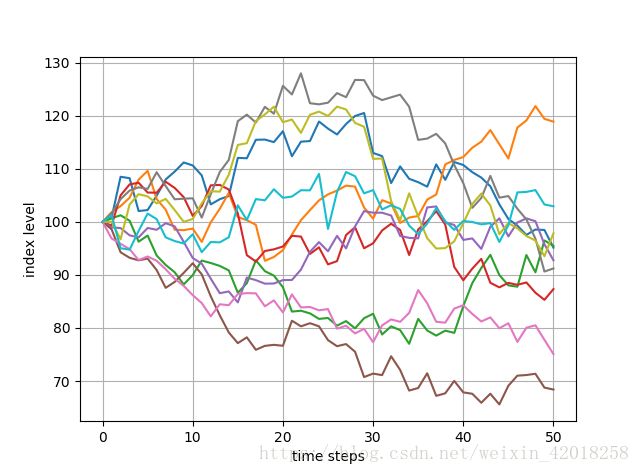
# 展示前10条模拟路径：
plt.plot(paths[:, :10])
plt.grid(True)
plt.xlabel('time steps')
plt.ylabel('index level')

几何布朗运动的10条模拟路程

我们主要感兴趣的是对数收益率的分布。

# 成一个包含所有对数收益率的ndaray对象
log_returns = np.log(paths[1:] / paths[0:-1])
# 考虑50个时间步上的第一条模拟路径
paths[:, 0].round(4)
# array([ 100.    ,  100.7527,  108.5193,  108.258 ,  102.0603,  102.2424,
#         104.9457,  108.018 ,  109.4967,  111.2178,  110.6562,  108.7809,
#         103.3086,  104.2923,  104.8908,  112.0843,  112.0133,  115.4933,
#         115.5401,  115.0547,  117.1103,  112.3911,  115.136 ,  115.2618,
#         118.937 ,  117.607 ,  116.4971,  118.4645,  119.9851,  120.5452,
#         113.0165,  112.4183,  107.3345,  110.4752,  108.1386,  107.5009,
#         106.6545,  110.8543,  107.9486,  111.291 ,  110.7415,  109.3914,
#         108.3647,  106.7219,  103.315 ,  100.5691,   99.2987,   97.5511,
#          98.5751,   98.4846,   95.1523])

# 模拟路径的对数收益率序列可能采取如下形式：
log_returns[:, 0].round(4)
# array([ 0.0075,  0.0743, -0.0024, -0.059 ,  0.0018,  0.0261,  0.0289,
#         0.0136,  0.0156, -0.0051, -0.0171, -0.0516,  0.0095,  0.0057,
#         0.0663, -0.0006,  0.0306,  0.0004, -0.0042,  0.0177, -0.0411,
#         0.0241,  0.0011,  0.0314, -0.0112, -0.0095,  0.0167,  0.0128,
#         0.0047, -0.0645, -0.0053, -0.0463,  0.0288, -0.0214, -0.0059,
#        -0.0079,  0.0386, -0.0266,  0.0305, -0.0049, -0.0123, -0.0094,
#        -0.0153, -0.0324, -0.0269, -0.0127, -0.0178,  0.0104, -0.0009,
#        -0.0344])

这是人们在金融市场上可能经历的：在一些日子里你的投资获得正收益。而在其他日子里。相对于最近的财富状况， 你损失了金钱。

def print_statistics(array):
    """
    Prints selected statistics
    :param array: object to generate statistic on
    :return: 
    """
    sta = scs.describe(array)
    print("%14s %15s" % ('statistic', 'value'))
    print(30 * "-")
    print("%14s %15.5f" % ('size', sta[0]))
    print("%14s %15.5f" % ('min', sta[1][0]))
    print("%14s %15.5f" % ('max', sta[1][1]))
    print("%14s %15.5f" % ('mean', sta[2]))
    print("%14s %15.5f" % ('std', np.sqrt(sta[3])))
    print("%14s %15.5f" % ('skew', sta[4]))
    print("%14s %15.5f" % ('kurtosis', sta[5]))

print_statistics(log_returns.flatten())# log_returns.flatten() 返回一个一维数组
#      statistic           value
# ------------------------------
#           size  12500000.00000
#            min        -0.15664
#            max         0.15371
#           mean         0.00060
#            std         0.02828
#           skew         0.00073
#       kurtosis         0.00068

本例中的数据集包含 1250 万个数据点， 其值主要处于 -0.15 和 0.15 之间。 我们预期的（设置的参数）平均年化收益为 0.05， 标准差（波动率）为 0.2。数据集中的年化值不完全等于上述值，但是很接近（均值乘以 50 ， 标准差乘以 50−−√ 50 ）。

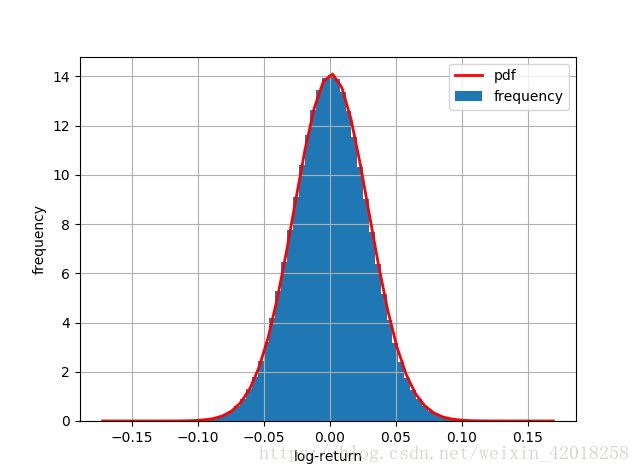
比较模拟对数收益率的分布和参数化 r 和 sigma 之后的正态分布概率密度函数（pdf）：

plt.hist(log_returns.flatten(), bins=70, normed=True, label='frequency')
plt.grid(True)
plt.xlabel('log-return')
plt.ylabel('frequency')
x = np.linspace(plt.axis()[0], plt.axis()[1])
plt.plot(x, scs.norm.pdf(x, loc=r / M, scale=sigma / np.sqrt(M)), 'r', lw=2.0, label='pdf')
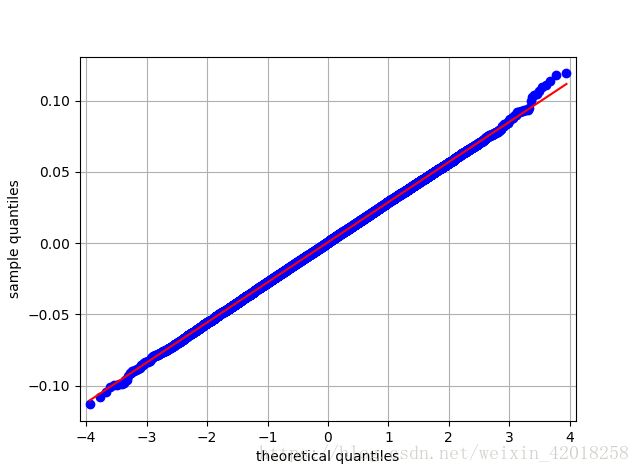
plt.legend()

对数收益率和正态密度函数的直方图

对比频率分布（直方图）与理论化 pdf 不是图形化 “检验” 正态性的唯一方法。所谓的分位数-分位数图（ qq 图）也很适合于这一任务：

sm.qqplot(log_returns.flatten()[::500], line='s')
plt.grid(True)
plt.xlabel('theoretical quantiles')
plt.ylabel('sample quantiles')

对数收益率的分位数-分位数图

尽管图形方法很有吸引力，但是它们通常无法代替更严格的测试过程：

偏斜度测试（skewtest）
测试样本的偏斜是否“正态”（也就是值足够接近0）

峰度测试（kurtosistest）
测试样本的峰度是否“正态”（也就是值足够接近0）

正态性测试（normaltest）
结合其他两种测试方法，检验正态性

def normality_tests(arr):
    """
    Tests for normality distribution of given data set
    :param arr: ndarray
    object to generate statistics on
    :return:
    """
    print("Skew of data set  %14.3f" % scs.skew(arr))
    print("Skew test p-value %14.3f" % scs.skewtest(arr)[1])
    print("Kurt of data set  %14.3f" % scs.kurtosis(arr))
    print("Kurt test p-value %14.3f" % scs.kurtosistest(arr)[1])
    print("Kurt test p-value %14.3f" % scs.normaltest(arr)[1])

normality_tests(log_returns.flatten())
# Skew of data set           0.001
# Skew test p-value          0.292
# Kurt of data set           0.001
# Kurt test p-value          0.625
# Norm test p-value          0.509

测试值表明， 对数收益率确实呈正态分布。

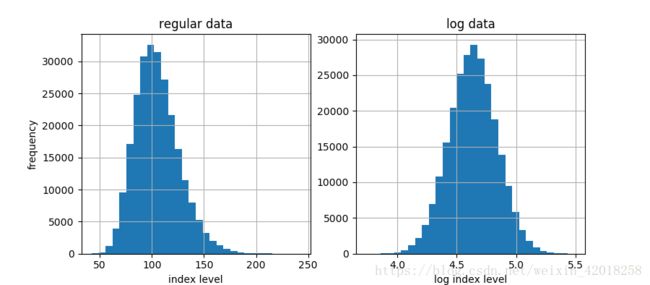
最后， 我们检查期末值是否确实呈正态分布。这也归结于正态性检验， 因为我们只需要应用对数函数转换数据（得到正态分布数据——也可能得不到）。

f, (ax1, ax2) = plt.subplots(1, 2, figsize=(9, 4))
ax1.hist(paths[-1], bins=30)
ax1.grid(True)
ax1.set_xlabel('index level')
ax1.set_ylabel('frequency')
ax1.set_title('regular data')
ax2.hist(np.log(paths[-1]), bins=30)
ax2.grid(True)
ax2.set_xlabel('log index level')
ax2.set_title('log data')

print_statistics(paths[-1])
#      statistic           value
# ------------------------------
#           size    250000.00000
#            min        42.19338
#            max       241.93670
#           mean       105.12602
#            std        21.22992
#           skew         0.61216
#       kurtosis         0.65952

数据集的统计数字和预期的表现一样，均值接近 105 ，标准（波动性）接近 20%

print_statistics(np.log(paths[-1]))
#      statistic           value
# ------------------------------
#           size    250000.00000
#            min         3.74226
#            max         5.48868
#           mean         4.63517
#            std         0.19996
#           skew        -0.00122
#       kurtosis         0.00128

对数指数水平的偏斜度和峰度也接近于0

normality_tests(np.log(paths[-1]))
# Skew of data set          -0.001
# Skew test p-value          0.803
# Kurt of data set           0.001
# Kurt test p-value          0.890
# Kurt test p-value          0.960

这个数据集也展现了高的p值， 为正态分布假设提供了很强的支持

再次比较频率分布和正态分布的 pdf

log_data = np.log(paths[-1])
plt.hist(log_data, bins=70, normed=True, label='observed')
plt.grid(True)
plt.xlabel('index levels')
plt.ylabel('frequency')
x = np.linspace(plt.axis()[0], plt.axis()[1])
plt.plot(x, scs.norm.pdf(x, log_data.mean(), log_data.std()), 'r', lw=2.0, label='pdf')
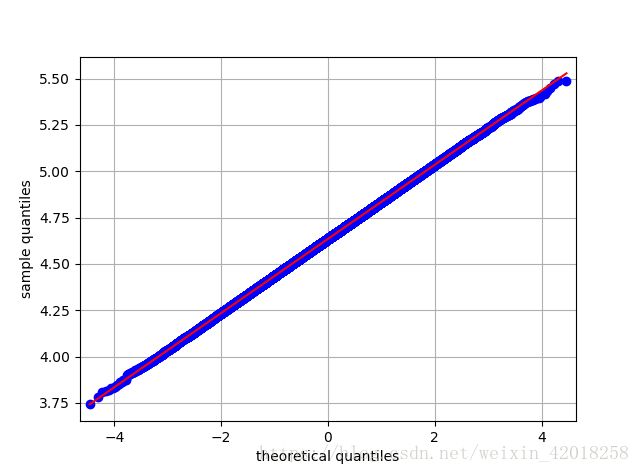
plt.legend()

对数指数水平和正态密度函数的直方图

sm.qqplot(log_data, line='s')
plt.grid(True)
plt.xlabel('theoretical quantiles')
plt.ylabel('sample quantiles')

11.1.2 现实世界的数据

从tushare中获取[上证指数，深证成指，中国卫星，中兵红箭]的数据

import pandas as pd
import tushare as ts
import datetime

symbols = ['sh000001', '399001', '600118', '000519']
indexes = pd.date_range('2016-01-01', '2018-07-06')
# 为了保持和从toshare获取的时间序列类型一致，这里把时间类型转为字符串
indexes = indexes.map(lambda x: datetime.datetime.strftime(x, '%Y-%m-%d'))

data = pd.DataFrame(index=indexes)
for sym in symbols:
    k_d = ts.get_k_data(sym, '2016-01-01', ktype='D')
    # 如果上面的时间序列不转成字符串，这里就要转成时间序列，以保持index类型一致
    # k_d['date'] = k_d['date'].astype('datetime64[ns]')
    k_d.set_index('date', inplace=True)
    data[sym] = k_d['close']
data = data.dropna()

data.info()
# 
# Index: 605 entries, 2016-01-04 to 2018-07-06
# Data columns (total 4 columns):
# sh000001    605 non-null float64
# 399001      605 non-null float64
# 600118      605 non-null float64
# 000519      605 non-null float64
# dtypes: float64(4)
# memory usage: 23.6+ KB

data.head()
#             sh000001    399001  600118  000519
# 2016-01-04   3296.66  11630.93  39.159   16.16
# 2016-01-05   3287.71  11468.06  40.072   17.45
# 2016-01-06   3361.84  11724.88  40.935   19.20
# 2016-01-07   3125.00  10760.27  37.034   17.28
# 2016-01-08   3186.41  10888.91  36.250   17.24

# 直接比较4个时间序列，但是规范化为起始值100
(data / data.ix[0] * 100).plot(figsize=(8, 6))

股票和指数水平在一段时间内的变动

# 计算对数收益率
log_returns = np.log(data / data.shift(1))
log_returns.head()
#             sh000001    399001    600118    000519
# 2016-01-04       NaN       NaN       NaN       NaN
# 2016-01-05 -0.002719 -0.014102  0.023048  0.076801
# 2016-01-06  0.022297  0.022147  0.021308  0.095571
# 2016-01-07 -0.073054 -0.085852 -0.100149 -0.105361
# 2016-01-08  0.019461  0.011884 -0.021397 -0.002317

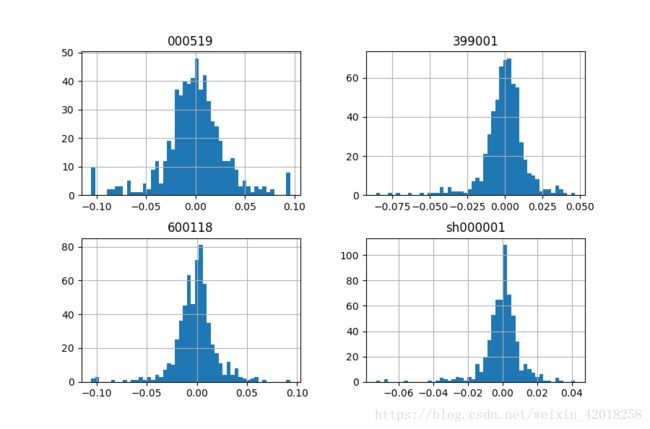
log_returns.hist(bins=50, figsize=(9, 6))

对数收益率直方图

下一步考虑时间序列数据集的不同统计数字：

for sym in symbols:
    print("\nResults for symbol %s" % sym)
    print(30 * "-")
    log_data = np.array(log_returns[sym].dropna())
    print_statistics(log_data)

# Results for symbol sh000001
# ------------------------------
#      statistic           value
# ------------------------------
#           size       604.00000
#            min        -0.07305
#            max         0.04174
#           mean        -0.00030
#            std         0.01077
#           skew        -1.65159
#       kurtosis         9.99414
# Results for symbol 399001
# ------------------------------
#      statistic           value
# ------------------------------
#           size       604.00000
#            min        -0.08585
#            max         0.04657
#           mean        -0.00044
#            std         0.01390
#           skew        -1.29898
#       kurtosis         6.60328
# Results for symbol 600118
# ------------------------------
#      statistic           value
# ------------------------------
#           size       604.00000
#            min        -0.10544
#            max         0.09334
#           mean        -0.00120
#            std         0.02069
#           skew        -0.75593
#       kurtosis         5.63994
# Results for symbol 000519
# ------------------------------
#      statistic           value
# ------------------------------
#           size       604.00000
#            min        -0.10555
#            max         0.09587
#           mean        -0.00121
#            std         0.03100
#           skew        -0.30928
#       kurtosis         2.34205

峰度值在所有4个数据集上都与正态分布的要求相去甚远。

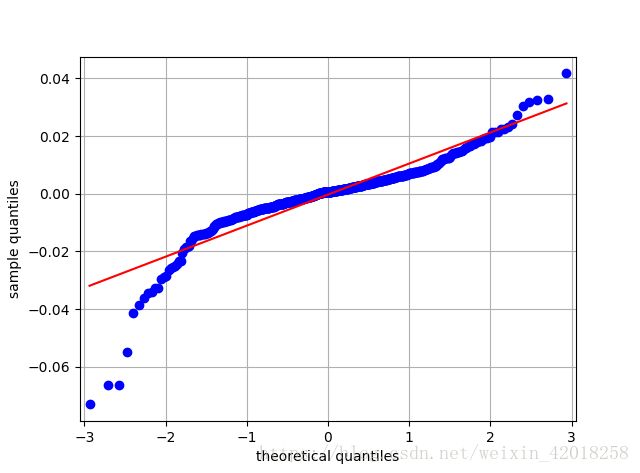
# 通过 qq 图检查 sh000001 的数据
sm.qqplot(log_returns['sh000001'].dropna(), line='s')
plt.grid(True)
plt.xlabel('theoretical quantiles')
plt.ylabel('sample quantiles')

上证指数 对数收益率分位数-分位数图

很显然，样本的分位数值不在一条直线上， 表明 “非正态性”。在左侧和右侧分别有许多值远低于和远高于直线。换言之，这一时间序列信息展现出 “大尾巴” （Fat tails） 。大尾巴一词指的是（频率）分布中观察到的正负异常值远多于正态分布应有表现的情况。

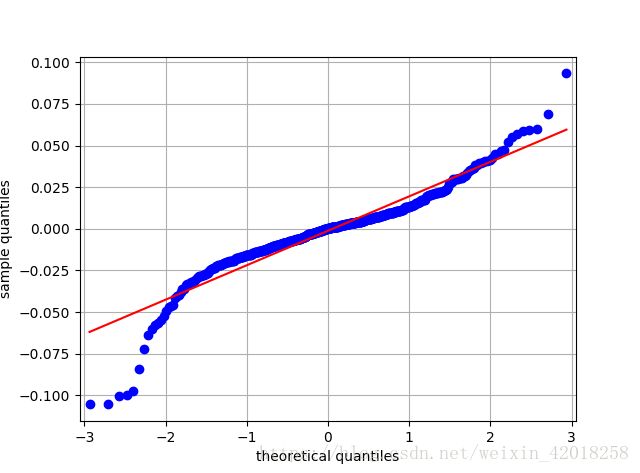
sm.qqplot(log_returns['600118'].dropna(), line='s')
plt.grid(True)
plt.xlabel('theoretical quantiles')
plt.ylabel('sample quantiles')

中国卫星 对数收益率分位数-分位数图

从中国卫星股票的数据，可以得出相同的结论 ， 分布中也有明显的 “大尾巴 ” 现象。

最后用上述结果进行正式的正态性检验：

for sym in symbols:
    print("\nResults for symbol %s" % sym)
    print(30 * "-")
    log_data = np.array(log_returns[sym].dropna())
    normality_tests(log_data)

# Results for symbol sh000001
# ------------------------------
# Skew of data set          -1.652
# Skew test p-value          0.000
# Kurt of data set           9.994
# Kurt test p-value          0.000
# Kurt test p-value          0.000
# Results for symbol 399001
# ------------------------------
# Skew of data set          -1.299
# Skew test p-value          0.000
# Kurt of data set           6.603
# Kurt test p-value          0.000
# Kurt test p-value          0.000
# Results for symbol 600118
# ------------------------------
# Skew of data set          -0.756
# Skew test p-value          0.000
# Kurt of data set           5.640
# Kurt test p-value          0.000
# Kurt test p-value          0.000
# Results for symbol 000519
# ------------------------------
# Skew of data set          -0.309
# Skew test p-value          0.002
# Kurt of data set           2.342
# Kurt test p-value          0.000
# Kurt test p-value          0.000

自始至终，不同测试的 p 值都为 0，强烈否决不同样板数据集呈正态分布的测试假设。这说明， 股票市场收益率的正态假设一一例如几何布朗运动模型中的假设一一通常无法证明是正确的，可能需要使用产生 “大尾巴”的更丰富模型（例如，跳跃扩散模型或者具备随机波动率的模型）。

未完待续……