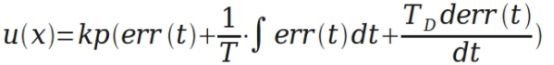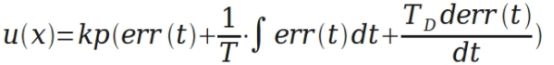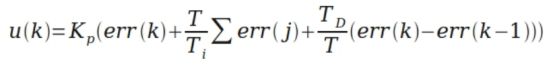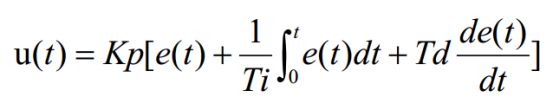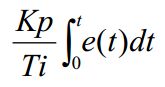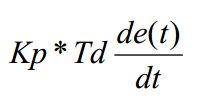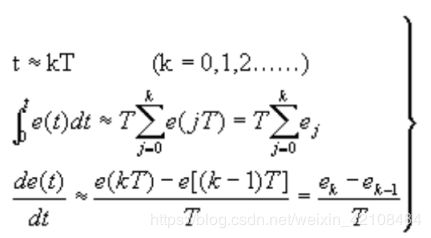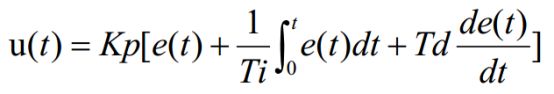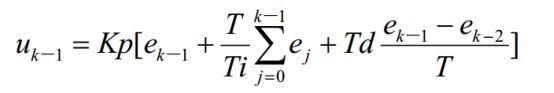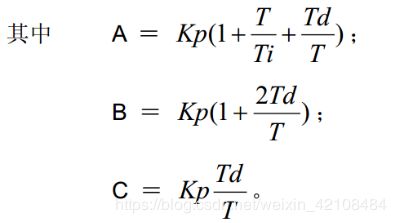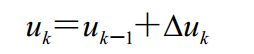1、PID的基本原理以及分类应用

本人以自己的学习过程以及参考别人笔记总结而来，将自己的经验写出来以供大家一起学习，如有错误请多指教

---

一、什么是PID

        PID控制器是工业过程控制中广泛采用的一种控制算法，其特点是结构简单灵活、技术成熟、适应性强。

        P、I、D分别为比例（Proportion）、积分（Integral）、微分（Differential）的简写；将偏差的比例、积分和微分通过线性组合构成控制量，用该控制量对受控对象进行控制，称为PID算法。总之，PID就是对输入偏差进行比例积分微分运算，运算的叠加结果去控制执行机构。在工程实践中，一般P是必须的，所以衍生出来很多的PID控制器，如PI、PD、PID等

1.1 PID 算法的一般形式： 

 

控制器本身就是比例、积分、微分三个环节的加和。这里我们规定（在 t 时刻）：
1.输入量为 r(t);
2.输出量为 c(t);
3.偏差量为 e(t)=rin(t)-rout(t); 

1.2 pid 的控制规律

连续状态的公式：

                                   

注意(以电机调速为例)：

    1.规定这个流程是用来为直流电机调速的;
    2.输入量 rin(t)为电机转速预定值;
    3.输出量 rout(t)为电机转速实际值;
    4.执行器为直流电机;
    5.传感器为光电码盘，假设码盘为 10 线;
   6.直流电机采用 PWM 调速 转速用单位 转/min 表示;

结论：
1.输入量 rin（t）为电机转速预定值（转/min）;
2. 输出量 rout(t)为电机转速实际值（转/min）;
3.偏差量为预定值和实际值之差（转/min）; 

1.3 PID整定口诀

                                                                        参数整定找最佳， 从小到大顺序查。
                                                                        先是比例后积分， 最后再把微分加。
                                                                        曲线振荡很频繁， 比例度盘要放大。
                                                                        曲线漂浮绕大弯， 比例度盘往小扳。
                                                                        曲线偏离回复慢， 积分时间往下降。
                                                                        曲线波动周期长， 积分时间再加长。
                                                                        曲线振荡频率快， 先把微分降下来。
                                                                        动差大来波动慢， 微分时间应加长。
                                                                        理想曲线两个波， 前高后低四比一。
                                                                        一看二调多分析， 调节质量不会低。

---

二、为什么要用到PID

       对一个控制系统而言，由于控制对象的精确数学模型难以建立，系统的参数经常发生变化，运用控制理论综合分析要耗费很大的代价，却不能得到预期的效果，所以人们往往采用PID调节器，根据经验在线整定参数，以便得到满意的控制效果。随着计算机特别是微机技术的发展，PID控制算法已能用微机简单实现，由于软件系统的灵活性，PID算法可以得到修正而更加完善。比如平衡小车，倒立摆，四轴飞行器，温度调节都用到了PID，可以说一切控制系统都可以用到PID。

---

三、PID控制器的离散化

1.说明一下反馈控制的原理，通过1.1的框图不难看出，PID 控制其实是对偏差的控制过程;
2.如果偏差为 0,则比例环节不起作用，只有存在偏差时，比例环节才起作用。
3.积分环节主要是用来消除静差，所谓静差，就是系统稳定后输出值和设定值之间的差值，积分环节实际上就是偏差累计的过程，把累计的误差加到原有系统上以抵消系统造成的静差。
4.而微分信号则反应了偏差信号的变化规律，或者说是变化趋势，根据偏差信号的变化趋势来进行超前调节，从而增加了系统的快速性 

根据PID连续状态公式

                                 

 

假设采样间隔为 T，则在第 K T 时刻：
        偏差 err(K)=rin(K)-rout(K);
        积分环节用加和的形式表示，即 err(K)+err(K+1)+……;
        微分环节用斜率的形式表示，即[err(K)-err(K-1)]/T;
从而形成如下 PID 离散表示形式：

                                    

则 u(K)可表示成为：

                                     

其实到这里为止，PID 的基本离散表示形式已经出来了。目前的这种表述形式属于位置型 PID，另外一种表述方式为增量式 PID，由 U 上述表达式可以轻易得到： 

                                      

那么：

                                   

       这就是离散化 PID 的增量式表示方式，由公式可以看出，增量式的表达结果和最近三次的偏差有关，这样就大大提高了系统的稳定性。需要注意的是最终的输出结果应该为
u(K)+增量调节值;
PID 的离散化过程基本思路就是这样，将离散化的公式转换成为 C 语言，从而实现微控制器的控制作用。

---

四、PID控制器的分类

4.1 模拟 PID 控制

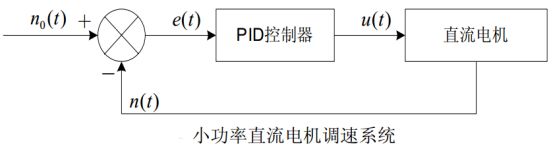
        模拟PID控制原理：如图所示是一个小功率直流电机的调速原理图。给定速度n0(t)与实际转n(t)速进行比较 ，其差值e(t) ，经过 PID 控制器调整后输出电压控制信号 ， 经过功率放大后，驱动直流电动机改变其转速。

                                 

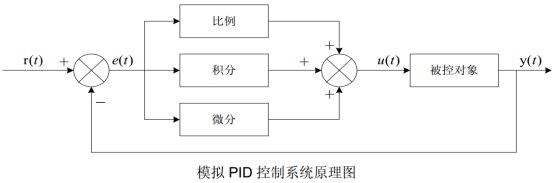
常规的模拟 PID 控制系统原理框图如下图所示：

                                    

        该系统由模拟 PID 控制器和被控对象组成。图中，r(t) 是给定值，y(t) 是系统的实际输出值，给定值与实际输出值构成控制偏差 e(t)：
                                 e(t) = r(t) - y(t)
e(t) 作为 PID 控制的输入， 作为 PID 控制器的输出和被控对象的输入。 所以模拟 PID 控制器的控制规律为

                                      

其中： Kp ―― 控制器的比例系数
            Ti ———控制器的积分时间，也称积分系数
            Td ―― 控制器的微分时间，也称微分系数

1）比例部分 

        作用是对系统瞬间产生的偏差进行快速修正，只有 P 时会有静差 。偏差一旦产生控制器立即产生控制作用， 使控制量向减少偏差的方向变化。比例部分的数学式表示是： 

                                                                                                Kp * e(t)

        注意：Kp是比例系数，Kp越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；但是越大，也越容易产生振荡，破坏系统的稳定性。故而，比例系数 选择必须恰当，才能过渡时间少，静差小而又稳定的效果。  

2）积分部分 

        作用是消除系统偏差，补偿系统的静差 ，只要存在偏差， 则它的控制作用就不断的增加； 只有在偏差 时， 它的积分才能是一个常数， 控制作用才是一个不会增加的常数。其数学式表示是： 

                                                                                       

        积分环节的调节作用虽然会消除静态误差，但也会降低系统的响应速度，增加系统的超调量。积分常数 越大， 积分的积累作用越弱， 这时系统在过渡时不会产生振荡； 但是增大积分常数 会减慢静态误差的消除过程，消除偏差所需的时间也较长， 但可以减少超调量，提高系统的稳定性。当Ti 较小时， 则积分的作用较强， 这时系统过渡时间中有可能产生振荡， 不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定Ti 。

3）微分部分 

        作用是加快调节过程，阻止偏差的变化， 偏差变化的越快， 微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入， 将有助于减小超调量， 克服振荡， 使系统趋于稳定， 特别对髙阶系统非常有利， 它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分， 或在微分起作用之
前先对输入信号进行滤波 ，其公式为：

                                                                                      

       Td 越大时， 则它抑制偏差 变化的作用越强； Td越小时，则它反抗偏差 变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分常数Td ，可以使微分作用达到最优。

4.2 数字 PID 控制 

4.2.1 位置式 PID 

        由于计算机控制是一种采样控制， 它只能根据采样时刻的偏差计算控制量，而不能像模拟控制那样连续输出控制量量， 进行连续控制。 由于这一特点式中的积分项和微分项不能直接使用，必须进行离散化处理。

        离散化处理的方法为：以T 作为采样周期， 作为采样序号，则离散采样时间 对应着连续时间 ， 用矩形法数值积分近似代替积分， 用一阶后向差分近似代替微分， 可作如下近似变换：

                                                 

上式中，为了表示的方便，将类似于 e(kT )简化成 ek 等。将此公式代入

                                 

可以得到离散的 PID 表达式为

                                

                                  

    上面两个式子意思一样，成为全量式或位置式 PID 控制算法

其中： k ―― 采样序号， k ＝0， 1， 2，……；
            uk ―― 第 k 次采样时刻的计算机输出值；
            ek ―― 第 k 次采样时刻输入的偏差值；
            ek－1 ―― 第 k －1 次采样时刻输入的偏差值；
             Ki ――积分系数， Ki＝Kp *T Ti ；
             Kd ――微分系数， Kd＝Kp *Td T ； 

         如果采样周期足够小，则上面的两式的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。

        算法的缺点是： 由于全量输出， 所以每次输出均与过去状态有关， 计算时要对 ek 进行累加，工作量大； 并且，因为计算机输出的 对应的是执行机构的实际位置， 如果计算机出现故障，输出的 将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实生产际中是不允许的。
       增量式 PID 控制算法可以避免着重现象发生。

4.2.2 增量式 PID  

        增量式 PID 是指数字控制器的输出只是控制量的增量∆uk 。 当执行机构需要的控制量是增量，而不是位置量的绝对数值时，可以使用增量式 PID 控制算法进行控制。

       增量式 PID 控制算法可以通过位置式离散PID 表达式推导出，可以得到控制器的第 k－1个采样时刻的输出值为：

                               

两式相减并整理，可得到增量式PID控制算法公式为：

                                 

                                          

        可以看出，如果计算机控制系统采用恒定的采样周期T ，一旦确定 A、 B、 C，只要使用前后三次测量的偏差值，就可以求出控制量。
       增量式 PID 控制算法与位置式 PID 算法相比，计算量小的多，因此在实际中得到广泛的应用。而位置式 PID 控制算法也可以通过增量式控制算法推出递推计算公式：

                                                                           

这就是目前在计算机控制中广泛应用的数字递推 PID 控制算法

4.3 控制器参数整定 

        PID控制器参数选择的方法很多，例如试凑法、临界比例度法、扩充临界比例度法等。但是，对于PID控制而言，参数的选择始终是一件非常烦杂的工作， 需要经过不断的调整才能得到较为满意的控制效果。依据经验，股 PID参数确定的步骤如下:

1）确定比例系数Kp

       确定比例系数Kp时，首先去掉PID的积分项和微分项，可以令Ti=0、Td=0, 使之成为纯比例调节。输入设定为系统允许输出最大值的60%~70%，比例系数Kp由0开始逐渐增大，直至系统出现振荡:再反过来，从此时的比例系数Kp逐渐减小，直至系统振荡消失。记录此时的比例系数Kp,设定PID的比例系数Kp为当前值的60% ~ 70%。

2)  确定积分时间常数Ti

       比例系数Kp确定之后，设定一个较 大的积分时间常数Ti,然后逐渐减小Ti,自至系统出现振荡，然后再反过来，逐渐增大Ti,直至系统振荡消失。记录此时的Ti.设定PID的积分时间常数Ti为当前值的150% ~、180%。

3)  确定微分时间常数Td

      微分时间常数Td一般不用设定，为0即可，此时PID调节转换为PI调节。如果需要设定，则与确定Ti的方法相同，取不振荡时其值的30%。

4)  系统空载、带载联调

      对PID参数进行微调，直到满足性能要求。

---