深层神经网络学习笔记——吴恩达deeplearning.ai学习笔记

深层神经网络学习笔记

1、神经网络中层数的定义和符号表示

这里需要对神经网络中所用到的符号进行定义，一个 L L 层的神经网络的定义为：

图1 神经网络层数定义

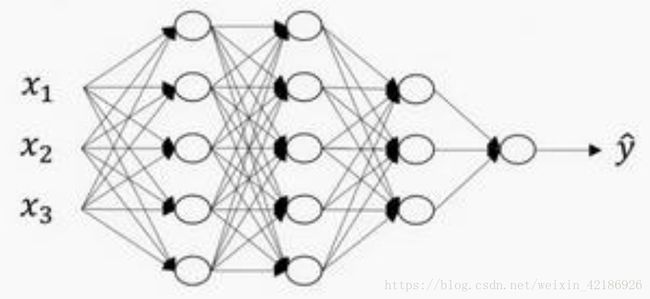
需要注意的是，输入层并不算神经网络的层数，只有隐藏层和输出层才算，例如上图中左侧的神经网络结构为3层，右侧的为6层，分别有2个隐藏层和5个隐藏层

图2 4层神经网络

如上图2所示，当 L=4 L = 4 时，神经网络共有3个隐藏层，其中第一层和第二层有5个神经元，第三层有三个神经元。这个神经网络有一下的符号表示：

第一层 n[1]=5 n [ 1 ] = 5 ，同理 n[2]=5 n [ 2 ] = 5 、 n[3]=3 n [ 3 ] = 3 ，这里 n[l] n [ l ] 表示第 l l 层中神经元的数量。每层中 a[l] a [ l ] 表示第 l l 层中的激活函数的结果，有 a[l]=g(zl) a [ l ] = g ( z l ) ，其中 z[l]=wla[l]+b[l] z [ l ] = w l a [ l ] + b [ l ] ， w[l] w [ l ] 第 l l 层的权重参数， b[l] b [ l ] 为偏置量。用于层数的表示方式是方括号上标 [] [ ]

2、前向传播和反向传播

对于神经网络，每一层都有正向传播和反向传播，首先讲解正向传播。

正向传播的输入是 a[l−1] a [ l − 1 ] ，输出是 a[l] a [ l ] ，缓存是 zl z l ；在实践的角度缓存中也要加上 wl w l 和 bl b l ，可以在其他环节中使用：

则前向传播的过程可以表示为： z[l]=wla[l−1]+b[l] z [ l ] = w l a [ l − 1 ] + b [ l ] 、 a[l]=g[l](z[l]) a [ l ] = g [ l ] ( z [ l ] )

使用向量化过程表示为： Z[l]=W[l]A[l−1]+b[l] Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] 、 A[l]=g[l](Z[l]) A [ l ] = g [ l ] ( Z [ l ] )

其中输入 X X 也就是 A[0] A [ 0 ] ，通过输入 X X 实现整个神经网络从左向右的传播。

接下来讲解反向传播过程。

反向传播过程输入为 da[l] d a [ l ] ，输出为 da[l−1] d a [ l − 1 ] 、 dw[l] d w [ l ] 、 db[l] d b [ l ] :

则反向传播过程可以整理为：

(1)

dz[l]=da[l]⋅g′(z[l]) d z [ l ] = d a [ l ] ⋅ g ′ ( z [ l ] )

(2) dw[l]=dz[l]⋅(a[l−1])T d w [ l ] = d z [ l ] ⋅ ( a [ l − 1 ] ) T

(3) db[l]=dz[l] d b [ l ] = d z [ l ]

(4) da[l−1]=(w[l])T⋅dz[l] d a [ l − 1 ] = ( w [ l ] ) T ⋅ d z [ l ]

再进行向量化之前，对反向传播进行一点解释：

这里的输入 da[l]=∂L∂a[l] d a [ l ] = ∂ L ∂ a [ l ] ，其中 L=ylog(a[l])+(1−y)log(1−a[l]) L = y log ⁡ ( a [ l ] ) + ( 1 − y ) log ⁡ ( 1 − a [ l ] ) ，即对于单个样本，这一函数表示的是一个交叉熵函数，而对于整个神经网络而言有：

J=1m∑i=1mL(i) J = 1 m ∑ i = 1 m L ( i )

这里出现的 1m 1 m 会在向量化的过程中出现一丝疑虑，注意在课程中的处理方式 da[l] d a [ l ] 并不是直接对 J J 进行求导，因为这样的话 da[l] d a [ l ] 中就会出现 1m 1 m ，从而使得 dw[l] d w [ l ] 以及其他变量的导数中不存在 1m 1 m 这一项。那么向量化后的 dA[l] d A [ l ] 是什么呢？向量化后的形式为：

dA[l]=[da[1](1),da[2](2),⋯，da[m](m)] d A [ l ] = [ d a [ 1 ] ( 1 ) , d a [ 2 ] ( 2 ) , ⋯ ， d a [ m ] ( m ) ]

即这一形式并未加上 1m 1 m 只是将 da[l] d a [ l ] 简单的进行了排列，所以会出现以下向量化后的表达形式：

dZ[l]=dA[l]⋅g′(Z[l])dW[l]=1mdZ[l]⋅(A[l−1])Tdb[l]=1mnp.sum(dZ[l],axis=1,keepdims=1)dA[l−1]=(W[l])T⋅dZ[l](1)(2)(3)(4) (1) d Z [ l ] = d A [ l ] ⋅ g ′ ( Z [ l ] ) (2) d W [ l ] = 1 m d Z [ l ] ⋅ ( A [ l − 1 ] ) T (3) d b [ l ] = 1 m n p . s u m ( d Z [ l ] , a x i s = 1 , k e e p d i m s = 1 ) (4) d A [ l − 1 ] = ( W [ l ] ) T ⋅ d Z [ l ]

根据 J J 的定义可知， dW[l] d W [ l ] 与 db[l] d b [ l ] 的值是需要进行 1m 1 m 操作的。

现在已经有了单层的前向传播和反向传播输入和输出，剩下的操作只需要根据层数进行操作即可，可使用for loop进行操作。

2.1、前向传播

前向传播的可表示为：

这里只能用一个显示for循环，从1到 L L 进行计算：

Z[l]=W[l]A[l−1]+b[l],A[l]=g[l](Z[l]) Z [ l ] = W [ l ] A [ l − 1 ] + b [ l ] , A [ l ] = g [ l ] ( Z [ l ] )

2.2、核对矩阵维数

神经网络中参数的维度为：

w[l],W[l] w [ l ] , W [ l ] 维度一样为 (n[l],n[l−1]) ( n [ l ] , n [ l − 1 ] )

b b 的维度为 (n[l],1) ( n [ l ] , 1 )

z[l],a[l] z [ l ] , a [ l ] 的维度为 (n[l],1) ( n [ l ] , 1 )

Z[l],A[l] Z [ l ] , A [ l ] 维度为 (n[l],m) ( n [ l ] , m )

dw[l],db[l] d w [ l ] , d b [ l ] 的维度和 w[l],b[l] w [ l ] , b [ l ] 维度一样

3、深层网络的好处

神经网络本就是针对非结构性数据而产生的一个算法，其根本特性也就是在每一层对数据进行特征提取。前几层网络只能学习一些低层次的简单特征，在后几层就把简单特征合并起来，去进行更深入的探测。所以前几层网络只是做一些简单的函数，而深层神经网络才可以拟合复杂的函数。

4、搭建神经网络结构

在之前的前向传播和反向传播中，介绍的是针对单个层的输入和输出，而利用单个层就可以搭建出一个完整的神经网络。

在搭建过程中要注意到缓存(cache)的作用，因为前向传播的过程中会产生出一些参数，这些参数在反向传播的计算中是会被用到的，所以要使用cache来进行存储。