线性动力学问题（二）

如果只是考虑对结构加载后的长期响应，那么做静力学分析就可以了。但是通常有的载荷作用时间很短，并且大小和方向属于不断变化的，如地震、旋转机械、热力透平等，由于叶轮在旋转的过程中受到流体的对它的交变载荷，因此需要对其进行动力学分析。以确保工作的可靠性。

1  介绍

动态模拟是将惯性力包含在动力学平衡方程中:

式中：

相当于牛顿第二定律中F=ma；

M是结构的质量；
是结构的加速度；
I是结构中的内力；
P是所施加的外力。
动态分析和静态分析最主要的不同在于平衡方程中包含惯性力项。
两者的另一个不同之处在于内力I的定义。

在静态分析中，内力仅由结构的变形引起;而动态分析中的内力包括运动(例如阻尼)和结构变形的共同贡献。

2  固有频率和模态

最简单的动力问题是在弹簧上的质量振动，如图1所示。

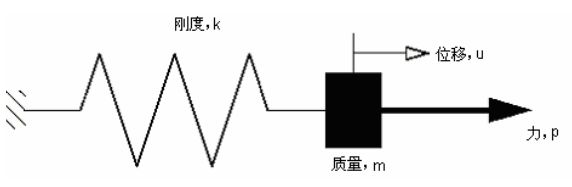图1 质量一弹簧系统

弹簧的内力为ku,所以运动方程为

（以质量为m的物体为研究对象不难求解）

这个质量弹簧系统的固有频率(单 位是弧度/秒)为：


若质量为m的物体被移动后再释放，它将以这个频率振动。假若以此频率施加一个动态外力，位移的幅度将剧烈增加，也就说所谓的共振现象。实际的结构具有多个固有频率，因此，在设计结构时避免使各固有频率与可能的荷载频率过分接近就很重要。固有频率可以通过分析结构在无荷载(动力平衡方程中的P =0 )时的动态响应而得到。此时，运动方程变为：

对于无阻尼系统，,则上式变为

这个方程解的形式为:

将此式代入到运动方程中便得到了特征值问题方程:

其中。
该系统具有n个特征值，此处n是有限元模型的自由度数。记为第j个特征值。它的平方根是结构的第j阶固有频率，并且是相应的第j阶特征向量。特征向量也就是所谓的模态(也称为振型)，因为它是结构在第j阶振型下的变形状态。
在有限元分析软件中只要给出所需振型的数目和所关心的最高频率即可。

2  振型叠加

在线性问题中，结构在荷载作用下的动力响应可以用固有频率和振型来表示，即结构的变形可以采用振型叠加的技术由各振型的组合得到，每阶模态都要乘以一个标量因子。 模型中位移矢量u被定义为：

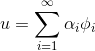
其中是振型的标量因子。模态叠加法只在模拟小变形、线弹性材料、无接触条件情况下是有效的，即必须是线性问题。
在结构动力学问题中，结构的响应往往取决于相对较少的前几阶振型，这使得模态叠加法在计算此类问题时特别有效。

如果一个含有10000个自由度的模型，则对运动方程的直接积分需要在每个时间点上求解10000个联立方程组。但若结构的响应采用100阶振型来描述，那么在每个时间步上只需求100个方程。更重要的是，振型方程是解耦的，而原来的运动方程是耦合的。
虽然在计算振型和频率时需要花费一些时间作为代价，但在计算响应时将节省大量的时间。

如果在模拟中存在非线性，在分析中固有频率会发生明显的变化，因此振型叠加法将不再适用。在这种情况下，需要对动力平衡方程直接积分，这将比振型分析要花费更多的时间。

具有下列特点的问题才适于进行线性瞬态动力学分析:

• 系统应该是线性的:线性材料特性，无接触条件，无非线性几何效应。
• 响应应该只受较少的频率支配。当响应中各频率成分增加时，例如撞击
• 和冲击问题，振型叠加技术的有效性将大大降低。
• 载荷的主要频率应在所提取的频率范围内，以确保对载荷的描述足够精
• 由于任何突然加载所产生的初始加速度应该能用特征模态精确描述。
• 系统的阻尼不能过大。

2  阻尼

无阻尼结构做自由振动，则它的振幅会保持恒定不变。

然而，但是现实中由于结构运动而耗散能量，振幅将逐渐减小直至振动停止，这种能量耗散称为阻尼。通常假定阻尼为粘滞的或正比于速度。动力平衡方程可以重新写成包含阻尼的形式为:

其中C是结构的阻尼阵，是结构的速度，即对位移求导du/dt。
能量耗散来自于诸多因素，其中包括结构结合处的摩擦和局部材料的迟滞效应。阻尼概念对于无需顾及能量吸收过程的细节表征而言是个很方便的方法。
在ABAQUS中，是针对无阻尼系统计算其振型的，然而，大多数工程问题还是包含阻尼的，尽管阻尼可能很小。有阻尼的固有频率和无阻尼的固有频率的关系：

其中：

临界阻尼比；
是是阻尼特征值；
c是该振型的阻尼；
c0是临界阻尼。
对较小的情形 (<0.1) ，有阻尼系统的特征频率非常接近于无阻尼系统的相应值。当增大时，采用无阻尼系统的特征频率就不太准确，当接近于1时，就不能采用无阻尼特征频率。当结构处于临界阻尼(=1) 时，施加一个扰动后，结构不会有往复摆动而是很快地恢复到静止的初始形态，如图2所示。

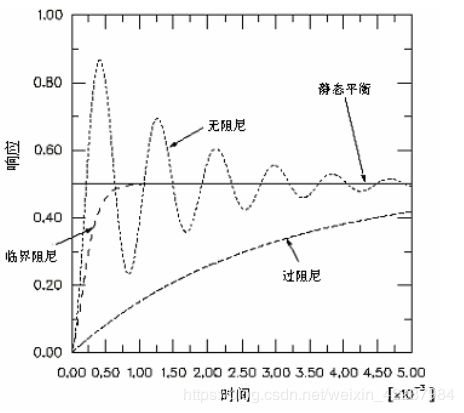图2  阻尼

2.1   ABAQUS 中阻尼的定义
在ABAQUS中，为了进行瞬时模态分析，可定义不同类型的阻尼:直接模态阻尼，瑞利(Rayleigh)阻尼和复合模态阻尼。模拟动力学过程要定义阻尼。阻尼是分析步定义的一部分，每阶振型可以定义不同数量的阻尼。
直接模态阻尼
采用直接模态阻尼可以定义对应于每阶振型的临界阻尼比。的典型取值范围是从1%到10%。直接模态阻尼允许精确定义每阶振型的阻尼。
Rayleigh阻尼
Rayleigh阻尼假设阻尼矩阵是质量矩阵和刚度矩阵的线性组合

其中和是用户定义的常数。尽管假设阻尼正比于质量和刚度没有严格的物理基础，但实际上我们对于阻尼的分布知之甚少，也就不能保证使用更为复杂的阻尼模型是正确的。一般来讲， 这个模型对于大阻尼系统——也就是临界阻尼超过10%时，是失效的。相对于其它形式的阻尼，可以精确地定义系统每阶模态的Rayleigh阻尼。

复合阻尼
复合阻尼中，可以定义每种材料的临界阻尼比，并且复合阻尼是对应于整体结构的阻尼。当结构中有许多不同种类材料时，这一选项是十分有用的。
2.2    阻尼值的选择
在大多数线性动力学问题中,恰当地定义阻尼对于获得精确的结果是十分重要的。但是阻尼只是对结构吸收能量这种特性的近似描述，而不是去仿真造成这种效果的物理机制。所以，确定分析中所需要的阻尼数据是很困难的。有时，可以从动力试验中获得这些数据，但是在多数情况下，不得不通过经验或参考资料获得数据。在这些情况下，要仔细地分析计算结果，应该通过参数分析来评价阻尼系数对于模拟的敏感性。

3  单元选择

ABAQUS的所有单元均可用于动力分析。选取单元的原则与静力分析相同。但是，在模拟冲击和爆炸载荷时，应选用一次单元。 因为它们具有集中质量公式，在模拟应力波效果方面优于采用二次单元的致质量公式。

4  网格划分

在动力分析中，剖分网格需要考虑响应中将被激发的振型，网格剖分应能充分反映那些振型。这就意味着，能满足静态模拟要求的网格，不一定能计算高频振型的动态响应。

在ABAQUES/Standard中还有其它几个采用振型叠加技术的线性动力分析。与模态动力程序计算的是时域上的响应不同，这些是计算频域上的结果。

5  稳态动力分析

稳态动力分析用于计算结构响应的振幅和相位，在ANSYS中叫做谐响应分析，其荷载是谐波激励形式，荷载的频率在用户给定的范围之内。

以下是些典型的例子:

• 汽车发动机底座在发动机运转速度范围内的响应。
• 旋转机械
• 飞机发动机的部件

6  反应谱

该分析主要用来求解结构承受固定端运动的动力作用时的峰值响应(位移、立力等)计算途径。 固定端的运动被称作为“基础运动”，地震引起地面运动就是一个例子。当设计目的是估计峰值响应时，这是一种被采用的典型方法。

7  随机响应

用于预测系统在承受随机连续激励时的响应。激励是采用统计意义上的能量谱密度函数来表示的。随机响应分析的例子如下:
飞机对扰动的响应。
结构对噪音的响应，例如来自喷气飞机的噪音。

总结

• 动力分析包括了结构的惯性效应。
• 频率提取程序可提取结构的自振频率和振型。通过振型叠加技术，可用振型确定线性系统的动力响应。这一方法尽管有效，但是不能用于非线性问题。
• 线性动力程序可以计算瞬态载荷下的瞬态响应、谐波载荷下的稳态响应、支座运动的峰值响应以及随机载荷的响应。
• 为了准确表现结构的动力特性，必须提取足够多的振型。运动方向上总的模态有效质量应占结构总的可运动质量的90%以上。
• 用户可以定义直接模态阻尼、Rayleigh 阻尼和复合模态阻尼。但是由于固有频率和振型的计算都是基于无阻尼的结构，所以只能分析低阻尼的结构。
• 模态技术不适用于非线性的动力分析。在这类分析中必须采用直接时间积分方法。
• 用振幅曲线可以定义任意的随时间变化的载荷和给定的边界条件。
• 振型和瞬态结果可以在ABAQUS/CAE的Visualization模块中用动画显示。