实现图的最短路径——Floyd算法的概述

Floyd算法的概述

Floyd算法是另一种经典的最短路径算法，将每个顶点作为源点，分别使用Dijkstra算法，Dijkstra算法是对单源点求得的最短路径，现在我们基于Dijkstra算法去实现对每一个顶点求得最短路径，此时我们使用的算法就是Floyd算法，即Floyd算法实现了全部结点到其他结点的最短路径。

Floyd算法的基本思想

Floyd算法是从带权的邻接矩阵起始，假设求Vi-Vj的最短路径，如果Vi-Vj有路径，通过图G.arc[i][j] 来表示路径的长度，但是此时的路径并不一定就是最短的，在此我们考虑在路径上添加另一个顶点$V0$ ，此时我们比较（$Vi$，$Vj$),($Vi$, $V0$, $Vj$ )这两条路径那条更短，通过dis[][]来表示更短的那条路径，此时找到的最短路径的含义就是$Vi$-$Vj$ 中间顶点序号不超过0的最短路径，那么下一次插入的中间顶点就应该是$V1$,此时比较的就是($Vi,...,V1,...,Vj$) 和 （$Vi$，$Vj$) 那个最短，此时求得了$ {Vi}$-${Vj}$ 中间顶点序号不超过1的最短路径，插入顶点重复依次累加，插入的顶点$V_0,V_1,...,V_{n-1}$迭代此过程，执行 n次此过程最终dis[][]表示求得任意两点之间的最短路径。

用一个简单的图理解保存D数组保存最短路径:

注意：点之间都$V_i-V_k$ 代表的 中间可能也经过 其他结点，所以连线之间有虚线表示，这个思想其实和Dijkstra思想是类似的~

同时还添加了保存前驱的Path[][]数组：

$Pat{h}_{k-1}[i][j]=b,Pat{h}_{k-1}[k][j]=a$, 如果存在$D_{k-1}[i][j]>D_{k-1}[i][k]+D_{k-1}[k][j]$的话，将$Pat{h}_{k-1}[i][j]=a$, 这里就是保存前驱，这里的Path和Dijkstra中的path 类似，只不过这个Path是二维数组

Floyd算法的基本步骤

• 假定一个$n$阶方阵序列，D^(-1), D⁽⁰⁾, D⁽¹⁾, D^(k) ……,D^(n-1). D^(-1)=G.arc[i][j],表示初始的从i到j的最短路径。

• 设D^(k-1)已经求出，如何得到D^(k)的是算法的关键，也是这个算法的主要 思想，Fylod算法的思想的到

  D^(k)[i][j] = MIN｛D^(k-1)[i][j]，D^(k-1)[i][k] + D^(k-1)[k][j]｝

  反复执行上述计算的公式可得到最短路径，最终 D^(n-1)[i][j]就是最$Vi$-$Vj$的最短路径。

Floyd算法的图解

同样的这次依然使用上次说到Dijkstra算法的使用图，看看使用Floyd算法，过程是怎么样的？

在此看一下数组两个数组每次的变换过程：

起始时：

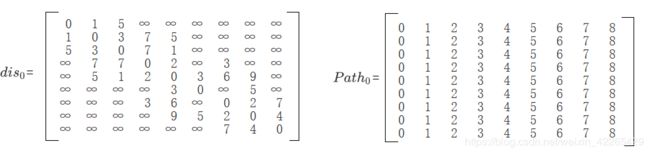
考虑顶点0时：

经过0的顶点没有更短的路径，两个数组没有变化。

考虑顶点1时：

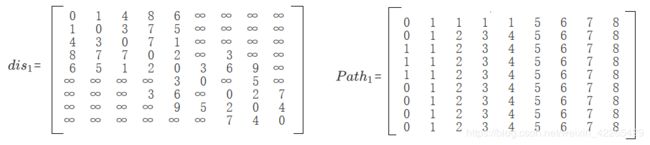
此时观察第一行，经过顶点1时，到其他结点的距离发生变化，此时$V_0-V_2,V_0-V_3,V_0-V_4$ 都更新了最短路径并且经过顶点$V_1$, 以后考虑的顶点依次递增，后面的就是同样的道理啦~

考虑顶点2时：

考虑顶点3，找出对应的最短路径，观察dis2 和path2

考虑顶点3时：

考虑顶点3，找出对应的最短路径，观察dis3 和path3

考虑顶点4时， 如下图：

考虑顶点4，找出对应的最短路径，观察dis4 和path4。

考虑顶点5时， 如下图：

考虑顶点5，找出对应的最短路径，观察dis5 和path5。

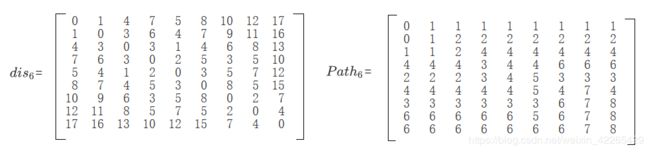
考虑顶点6时， 如下图：

考虑顶点6，找出对应的最短路径，观察dis6 和path6。

考虑顶点7时， 如下图：

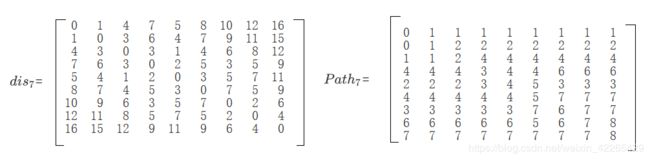
考虑顶点7，找出对应的最短路径，观察dis7 和path7。

考虑顶点8时， 如下图：

考虑顶点8，找出对应的最短路径，观察dis8 和path8，这是最后一次查询顶点，按照刚刚说的算法的思想，一次查询顶点​​$V_1,V_2,...,V_{n-1}$ 在这个图中最后一个就是$V_8$,一共比较了9次，找到每个顶点之间的最短路径。

Floyd算法的实现过程

Floyd算法是通过三个 for循环实现的。

for(int k = 0; k < n; k++)
    for(int i = 0; i < n; i++)
        for(int j = 0; j < n; j++)

满足刚刚所说的思想:D^(k-1)[i][j] = MIN｛D^(k-1)[i][j]，D^(k-1)[i][k] + D^(k-1)[k][j]｝ 具体实现就是：dis[i][k] + dis[k][j] < dis[i][j]时， dis[i][j] = dis[i][k] + dis[k][j]。

void Floyd(Graph G){
    int dis[MAX_VEX][MAX_VEX], path[MAX_VEX][MAX_VEX];
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex; j++){
            if(i != j) dis[i][j] = G.arc[i][j];
            else dis[i][j] = 0;
            path[i][j] = j;
        }
    }
    for(int k = 0; k < G.numvex; k++){
        for(int i = 0; i < G.numvex; i++){
            for(int j = 0; j < G.numvex; j++){
                if(dis[i][k] + dis[k][j] < dis[i][j]){
                    dis[i][j] = dis[i][k] + dis[k][j];
                    path[i][j] = path[i][k];
                }
            }
        }
    }

Floyd算法的完整实现过程

#include 
#include 
#define MAX_VEX 100
#define INF 65535

using namespace std;
struct Graph{
    char vexs[MAX_VEX];
    int arc[MAX_VEX][MAX_VEX];
    int numvex,numarc;
};
void CreateGraph(Graph &G){
    int vi, vj, w;
    cout << "please enter the number of vertexes and arcs : \n";
    cin >> G.numvex >> G.numarc;
    for(int i = 0; i < G.numvex; i++){
        printf("Please enter the NO.%d name of vex : ",i+1);
        cin >> G.vexs[i];
    }
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex ;j++){
            G.arc[i][j] = INF;
        }
    }
    cout << endl;
    for(int i = 0; i < G.numarc; i++){
        cout<< "Enter the subscripts and weights from vertex vi to vertex vj : ";
        cin >> vi >> vj >> w;
        G.arc[vi][vj] = w;
        G.arc[vj][vi] = w;
    }
}
void Floyd(Graph G){
    int dis[MAX_VEX][MAX_VEX], path[MAX_VEX][MAX_VEX];
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex; j++){
            if(i!= j) dis[i][j] = G.arc[i][j];
            else dis[i][j] = 0;
            path[i][j] = j;
        }
    }
    for(int k = 0; k < G.numvex; k++){
        for(int i = 0; i < G.numvex; i++){
            for(int j = 0; j < G.numvex; j++){
                if(dis[i][k] + dis[k][j] < dis[i][j]){
                    dis[i][j] = dis[i][k] + dis[k][j];
                    path[i][j] = path[i][k];
                }
            }
        }
    }
    //输出Floyd算法构成的最短路径,z在这里使用的是临时变量数组的方式
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex; j++) printf("%3d ",dis[i][j]);
        cout << endl;
    }
    cout << endl;
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex; j++) printf("%3d ",path[i][j]);
        cout << endl;
    }
}
void DispalyGraph(Graph G){
    for(int i = 0; i < G.numvex; i++)
        printf("%c ", G.vexs[i]);
        cout << endl;
    for(int i = 0; i < G.numvex; i++){
        for(int j = 0; j < G.numvex; j++){
            if(G.arc[i][j] == INF) printf("%6s", "∞");
            else printf("%6d", G.arc[i][j]);
        }
        cout << endl;
    }
}
int main(){
    Graph G;
    CreateGraph(G);
    DispalyGraph(G);
    Floyd(G);
    return 0;
}
/*
0 1 1
0 2 5
1 3 7
1 4 5
4 2 1
2 3 7
3 6 3
6 4 6
4 7 9
7 5 5
6 8 7
7 8 4
1 2 3
3 4 2
4 5 3
6 7 2
*/

分析

在代码中也可以看出Floyd算法的时间复杂度时$O(n^3)$,时间复杂度较高，效率比较低~~

总结

基本最短路径算法就这两种Dijkstra， Floyd 这两种算法，还有 画图不容易 ，觉得有帮助就给赞吧~~ 你的认可是俺前进的动力~~ 。还有就是带有权值为负的最短路径算法Bellman_Ford，以及优化的SPFA算法，之后会提到。