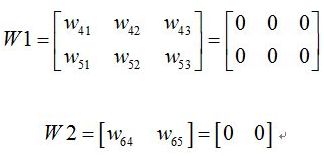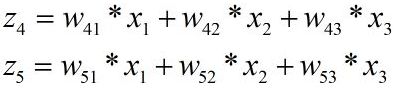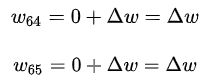神经网络参数初始化总结分析

神经网络的参数主要是权重（weights）：W， 和偏置项（bias）：b。

训练神经网络的时候需先给定一个初试值，才能够训练，然后一点点地更新，但是不同的初始化方法，训练的效果可能会截然不同。

 

目录

 

1、全0初始化

2、全相同参数初始化

3、正态分布随机初始化

1）使用较小的随机值初始化

2）使用较大的随机值初始化

3）选择合适的随机值进行初始化

4）讨论

5、Xavier初始化

6、He Initialization初始化

---

代码下载，没有链接的小伙伴也可以在评论中留下你的邮箱，我稍后发给你：

https://download.csdn.net/download/weixin_42521239/12090042

---

 

1、全0初始化

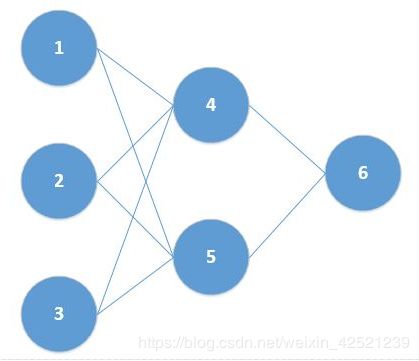
假设我们现在需要初始化的神经网络如下所示：

 我们初始化权值为

其中W1代表输入层到隐藏层的权值矩阵，W2代表隐藏层到输出层的权值矩阵。

假设网络的输入为[x1,x2,x3]，然后通过网络的正向传播，可以得出：

故

从上面可以知道，此时隐藏层的值是相同的，然后经过激活函数f后，得到的输出仍然是相同的，

可以知道，通过反向传播后，结点4,5的梯度改变是一样的，假设都是,那么此时结点4与结点6之间的参数，与结点5与结点6之间的参数变为了如下：

由上式可以看出，新的参数相同了！！！！

同理可以得出输入层与隐藏层之间的参数更新都是一样的，得出更新之后的参数

都是相同的！然后不管进行多少轮正向传播以及反向传播，每俩层之间的参数都是一样的。

换句话说，本来我们希望不同的结点学习到不同的参数，但是由于参数相同以及输出值都一样，不同的结点根本无法学到不同的特征！这样就失去了网络学习特征的意义了。

隐藏层与其它层多个结点，其实仅仅相当于一个结点！！

这样总结来看：w初始化全为0，很可能直接导致模型失效，无法收敛。

因此可以对w初始化为随机值解决（在cnn中，w的随机化，也是为了使得同一层的多个filter，初始w不同，可以学到不同的特征，如果都是0或某个值，由于计算方式相同，可能达不到学习不同特征的目的）

下面根据代码验证全0初始化对训练结果的影响

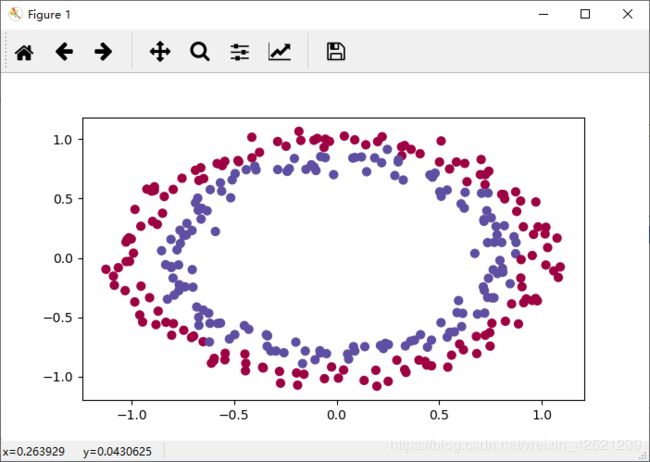
利用全连接网络对两堆点进行分类。

前向神经网络构建

def forward_propagation(X, parameters):
    """
    Implements the forward propagation (and computes the loss) presented in Figure 2.
    
    Arguments:
    X -- input dataset, of shape (input size, number of examples)
    Y -- true "label" vector (containing 0 if cat, 1 if non-cat)
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
                    W1 -- weight matrix of shape ()
                    b1 -- bias vector of shape ()
                    W2 -- weight matrix of shape ()
                    b2 -- bias vector of shape ()
                    W3 -- weight matrix of shape ()
                    b3 -- bias vector of shape ()
    
    Returns:
    loss -- the loss function (vanilla logistic loss)
    """
        
    # retrieve parameters
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"]
    
    # LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
    z1 = np.dot(W1, X) + b1
    a1 = relu(z1)
    z2 = np.dot(W2, a1) + b2
    a2 = relu(z2)
    z3 = np.dot(W3, a2) + b3
    a3 = sigmoid(z3)
    
    cache = (z1, a1, W1, b1, z2, a2, W2, b2, z3, a3, W3, b3)
    
    return a3, cache

全0初始化

def initialize_parameters_zeros(layers_dims):
    """
    将模型的参数全部设置为0

    参数：
        layers_dims - 列表，模型的层数和对应每一层的节点的数量
    返回
        parameters - 包含了所有W和b的字典
            W1 - 权重矩阵，维度为（layers_dims[1], layers_dims[0]）
            b1 - 偏置向量，维度为（layers_dims[1],1）
            ···
            WL - 权重矩阵，维度为（layers_dims[L], layers_dims[L -1]）
            bL - 偏置向量，维度为（layers_dims[L],1）
    """
    parameters = {}

    L = len(layers_dims)  # 网络层数

    for l in range(1, L):
        parameters["W" + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))
        parameters["b" + str(l)] = np.zeros((layers_dims[l], 1))

        # 使用断言确保我的数据格式是正确的
        assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
        assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))

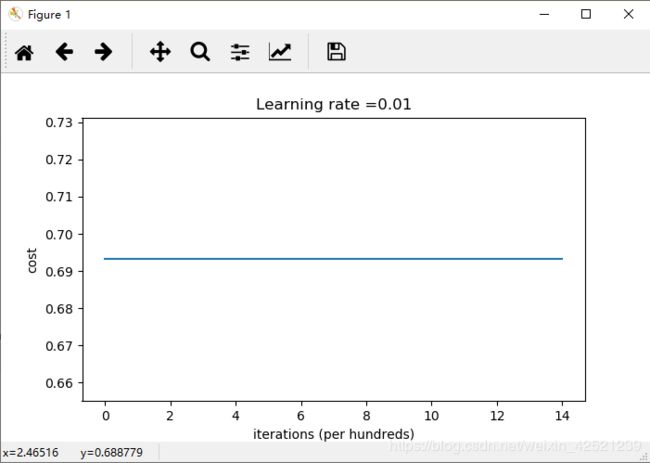
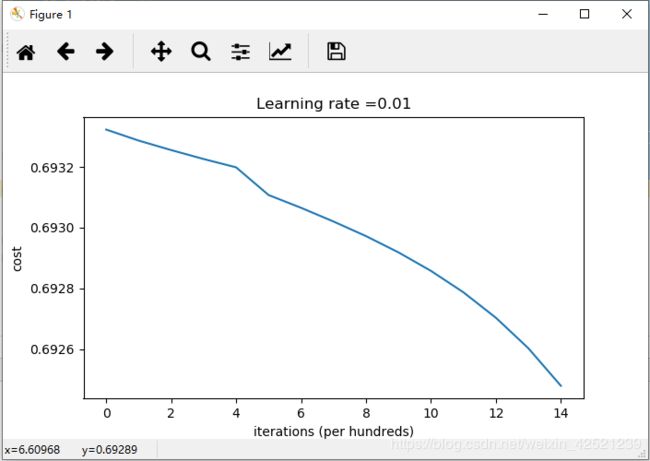
    return parameters

 损失函数值为

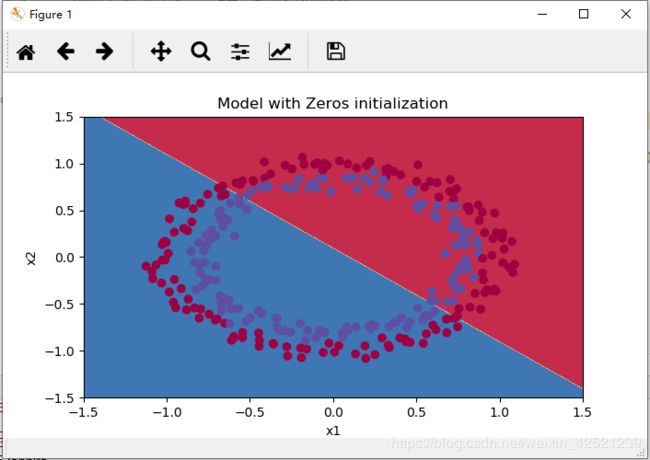
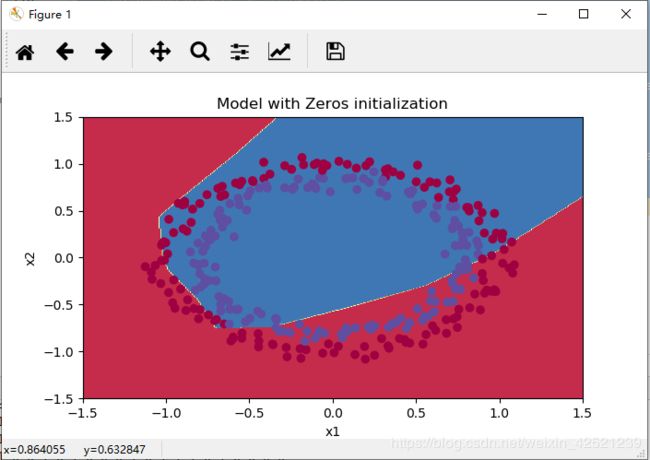
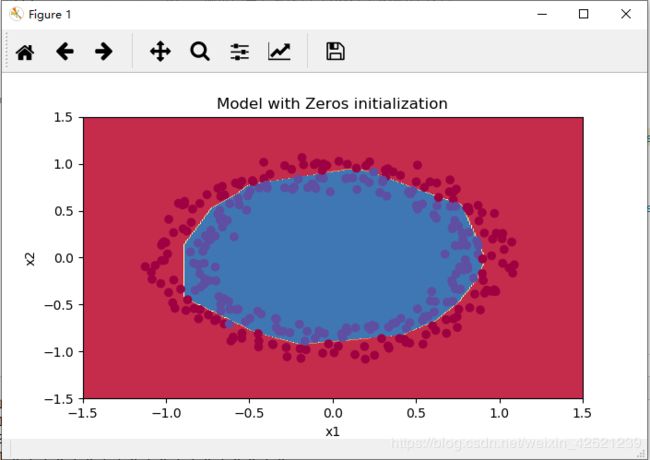
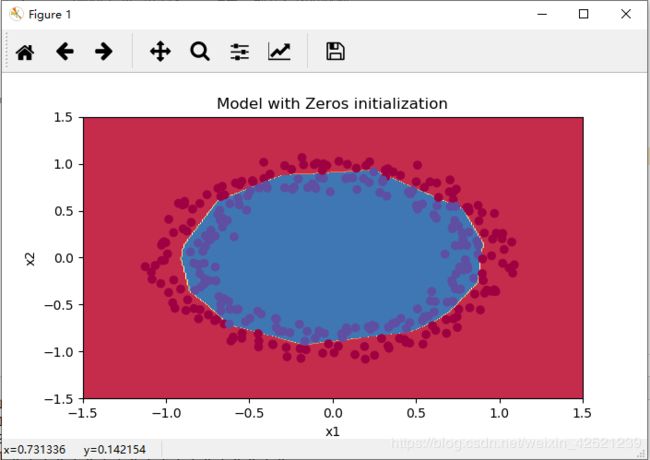
可以发现，压根就没训练！得到的模型跟瞎猜没有区别。

且损失函数的值一直保持在0.69左右，为什么是0.69

因为log0.5=0.69，也就是说，前向神经网络的输出就是0.5,0.5，损失函数值一直保持不变，也就意味着神经网络的更新根本没有起作用。

不管是哪个神经元，它的前向传播和反向传播的算法都是一样的，如果初始值也一样的话，不管训练多久，它们最终都一样，都无法打破对称（fail to break the symmetry）,那每一层就相当于只有一个神经元，最终L层神经网络就相当于一个线性的网络，如Logistic regression，线性分类器对我们上面的非线性数据集是“无力”的，所以最终训练的结果就瞎猜一样。

2、全相同参数初始化

如果全0参数初始化，用全相同参数初始化也导致了不管进行多少轮正向传播以及反向传播，每俩层之间的参数都是一样的。

我们将神经网络全部初始化为一个相同的常数，例如全部初始化为1。

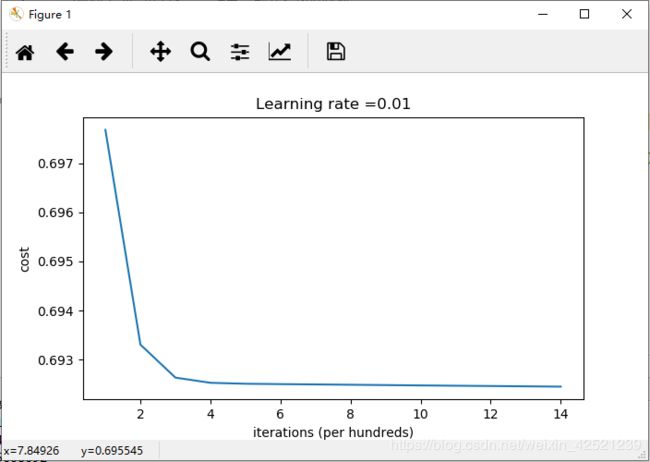
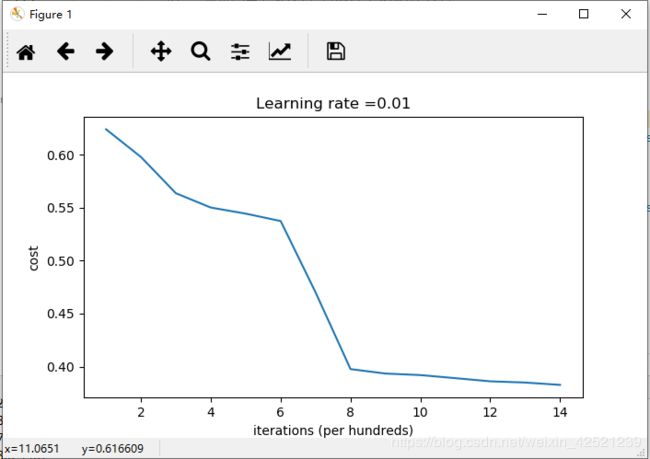
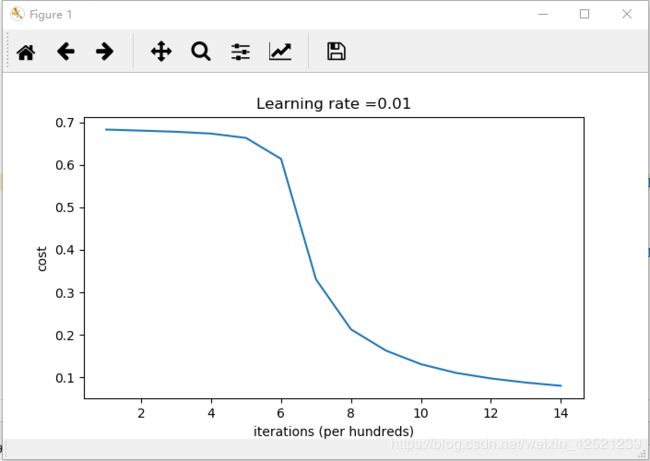
进行全相同参数初始化后的loss值曲线为

 仔细观察，损失值在0.698时开始下降，下降到不足0.692时就基本不动了，前向神经网络的输出依然是保持在0.5，0.5左右。

 

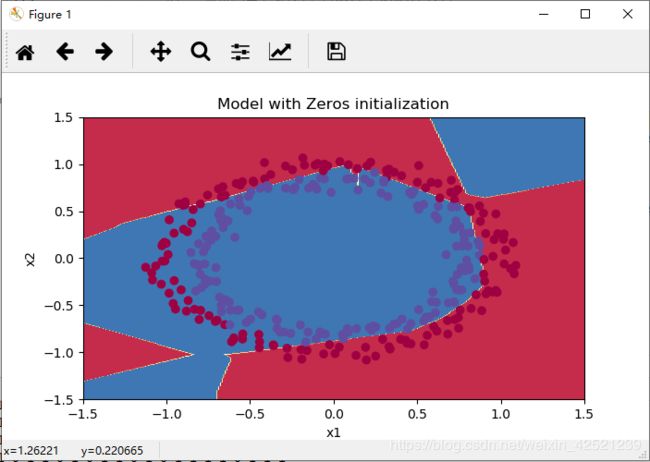
 分类结果依然是分了等于没分。

因此，全相同参数初始化与全零初始化一样，都无法打破神经网络的参数对称性，无法得到正确的训练结果。

3、正态分布随机初始化

1）使用较小的随机值初始化

def initialize_parameters_random(layers_dims):
    """
    参数：
        layers_dims - 列表，模型的层数和对应每一层的节点的数量
    返回
        parameters - 包含了所有W和b的字典
            W1 - 权重矩阵，维度为（layers_dims[1], layers_dims[0]）
            b1 - 偏置向量，维度为（layers_dims[1],1）
            ···
            WL - 权重矩阵，维度为（layers_dims[L], layers_dims[L -1]）
            b1 - 偏置向量，维度为（layers_dims[L],1）
    """

    np.random.seed(3)  # 指定随机种子
    parameters = {}
    L = len(layers_dims)  # 层数

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) *0.1  # 使用10倍缩放
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

        # 使用断言确保我的数据格式是正确的
        assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
        assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))

    return parameters

可以看到loss曲线为

再看分类效果

2）使用较大的随机值初始化

def initialize_parameters_random(layers_dims):
    """
    参数：
        layers_dims - 列表，模型的层数和对应每一层的节点的数量
    返回
        parameters - 包含了所有W和b的字典
            W1 - 权重矩阵，维度为（layers_dims[1], layers_dims[0]）
            b1 - 偏置向量，维度为（layers_dims[1],1）
            ···
            WL - 权重矩阵，维度为（layers_dims[L], layers_dims[L -1]）
            b1 - 偏置向量，维度为（layers_dims[L],1）
    """

    np.random.seed(3)  # 指定随机种子
    parameters = {}
    L = len(layers_dims)  # 层数

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 10  # 使用10倍缩放
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

        # 使用断言确保我的数据格式是正确的
        assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
        assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))

    return parameters

损失函数值loss值曲线为

分类效果为

3）选择合适的随机值进行初始化

def initialize_parameters_random(layers_dims):
    """
    参数：
        layers_dims - 列表，模型的层数和对应每一层的节点的数量
    返回
        parameters - 包含了所有W和b的字典
            W1 - 权重矩阵，维度为（layers_dims[1], layers_dims[0]）
            b1 - 偏置向量，维度为（layers_dims[1],1）
            ···
            WL - 权重矩阵，维度为（layers_dims[L], layers_dims[L -1]）
            b1 - 偏置向量，维度为（layers_dims[L],1）
    """

    np.random.seed(3)  # 指定随机种子
    parameters = {}
    L = len(layers_dims)  # 层数

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * 2  # 使用10倍缩放
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

        # 使用断言确保我的数据格式是正确的
        assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
        assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))

    return parameters

训练的loss值曲线为

分类效果为

4）讨论

显然，使用随机值初始化可以很好的打破神经网络的对称性，但是不管是使用过大的随机值初始化和过小的随机值初始化，其最后收敛到的loss值都比较大。

只有使用了合适的随机初始值进行初始化，才能较好的实现正确的分类。

当我们使用较小的随机值进行初始化时，我们可以认为这些较小的随机值都比较接近于0。深度学习中，我们认为参数越大，模型越复杂；参数越小，模型越简单。所以我们使用较小的初始值时，模型的太简单了，所以实现效果不好。

那么为什么随机初始值较大，也会导致模型收敛得不好呢。我们可以看我们使用的激活函数relu

对于激活函数relu而言，中间的斜率大，两边的斜率小还趋于0,。所以当我们把随机的值乘以10以后，我们的初值就会往两边跑，那么就是出现梯度消失的现象，迭代次数再多，损失函数也只能下降一点点，或者干脆一点都不下降。

5、Xavier初始化

Xavier初始化的基本思想是，若对于一层网络的输出和输出可以保持正态分布且方差相近，这样就可以避免输出趋向于0，从而避免梯度弥散情况。

• 条件：正向传播时，激活值的方差保持不变；反向传播时，关于状态值的梯度的方差保持不变。
• 初始化方法：

• 假设激活函数关于0对称，且主要针对于全连接神经网络。适用于tanh和softsign。

• 

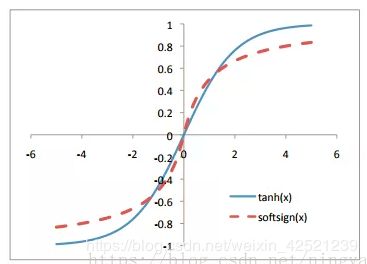
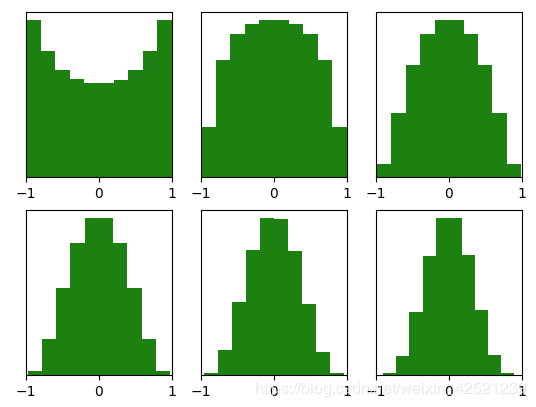
 例如，对于激活函数tanH ，Xavier initialization后每层的激活函数输出值的分布：

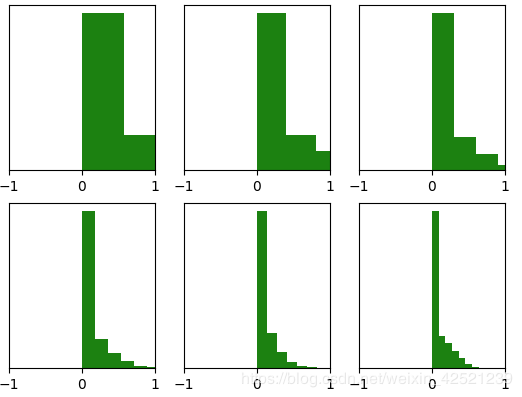
能够看出，深层的激活函数输出值还是非常漂亮的服从标准高斯分布。虽然Xavier initialization能够很好的 tanH 激活函数，但是对于目前神经网络中最常用的ReLU激活函数，还是无能能力，请看下图： 

当达到5，6层后几乎又开始趋向于0，更深层的话很明显又会趋向于0。 

 

6、He Initialization初始化

对于前面使用随机值进行初始化的方式，我们可以发现，过大或者过小的初始参数都会使得神经网络难以训练，但是，当选择了合适大小的随机值时，效果还是不错的，因为如何选择一个合适的随机值就成了关键。

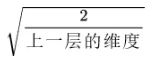
论文He et al., 2015.中提出了一种方法，我们称之为He Initialization，它就是在我们随机初始化了之后，乘以

这样就避免了参数的初始值过大或者过小，因此可以取得比较好的效果，代码也很简单。

同时，He Initialization还能解决Xavier Initialization的问题。

• 条件：正向传播时，状态值的方差保持不变；反向传播时，关于激活值的梯度的方差保持不变。
• 适用于ReLU的初始化方法

• 适用于Leaky ReLU的初始化方法：

其中，hi,wi分别表示卷积层中卷积核的高和宽，而di表示当前层卷积核的个数。

def initialize_parameters_he(layers_dims):
    """
    参数：
        layers_dims - 列表，模型的层数和对应每一层的节点的数量
    返回
        parameters - 包含了所有W和b的字典
            W1 - 权重矩阵，维度为（layers_dims[1], layers_dims[0]）
            b1 - 偏置向量，维度为（layers_dims[1],1）
            ···
            WL - 权重矩阵，维度为（layers_dims[L], layers_dims[L -1]）
            b1 - 偏置向量，维度为（layers_dims[L],1）
    """

    np.random.seed(3)  # 指定随机种子
    parameters = {}
    L = len(layers_dims)  # 层数

    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))

        # 使用断言确保我的数据格式是正确的
        assert (parameters["W" + str(l)].shape == (layers_dims[l], layers_dims[l - 1]))
        assert (parameters["b" + str(l)].shape == (layers_dims[l], 1))

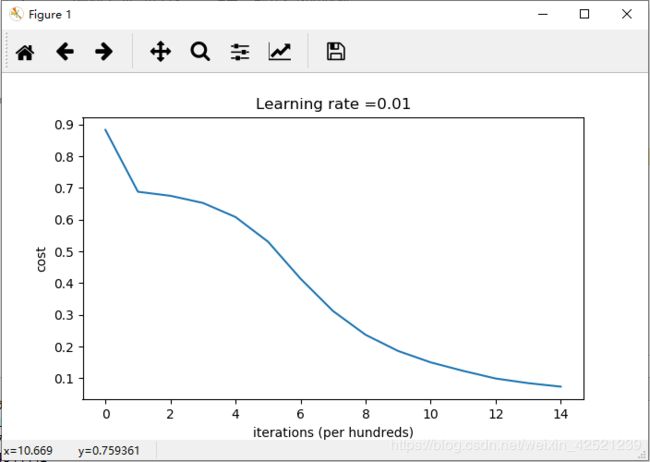
    return parameters

损失函数的loss曲线为

分类的效果为

可以看到He Initialization由于是基于随机值初始化的，所以能够很好地打破神经网络的对称性问题，同时，又解决了随机值过大或者过小的问题，可以较好的学习。