数据结构学习笔记——栈和队列
目录
- (一)栈的定义
- (二)栈的基本操作
- (三)栈的顺序存储结构及实现
- 1、栈的顺序存储结构——进栈操作
- 2、栈的顺序存储结构——出栈操作
- (四)两栈共享空间
- (五)栈的链式存储结构及实现
- 1、栈的链式存储结构——进栈操作
- 2、栈的链式存储结构——出栈操作
- (六)队列的定义
- (七)队列的基本操作
- (八)循环队列
- 1、顺序队列的不足
- 2、顺序队列定义及操作
- (九)队列的链式存储及实现
ps:此文章只是为了总结学习数据结构笔记,便于以后忘记查阅,因此部分图片会借用书上的图片,望理解。
(一)栈的定义
栈( stack )是限定仅在表尾进行插入和删除操作的线性表。,我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈。栈又称为后进先出(Last In First Out)的线性表,简称LIFO结构。
栈的插入操作,叫做进栈,也称压栈,入栈。如下图所示:

栈的删除操作,也叫出栈,也有的叫弹栈,如上图所示。
(二)栈的基本操作
ADT 栈(stack)
Data
同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系。
Operation
InitStack ( *S ):初始化操作.建立一个空栈S。
DestroyStack ( *S ):若栈存在,則销毁它。
ClearStack (*S):将栈清空。
StackEmpty ( S ):若栈为空,返回true,否則返回 false。
GetTop (S,*e):若栈存在且非空,用e返回S的栈顶元素。
Push (*S,e):若栈S存在,插入新元素e到栈S中并成为栈頂元素。
Pop (*S,*e):删除栈S中栈顶元素,并用e返回其值。
StackLength (S):返回回栈S的元素个数。
endADT
因为栈的本身是一个线性表,因此上一节所讨论的线性表的顺序存储和链式存储对于栈也同样适用。
(三)栈的顺序存储结构及实现
通常定义一个top变量来只是栈顶元素在数组中的位置,当栈存在一个元素时,top等于0,英雌通常把空栈的判定条件定为top等于-1。
栈的结构定义:
/* 顺序栈结构 */
typedef int SElemType; /* SElemType类型根据实际情况而定,这里假设为int */
typedef struct
{
SElemType data[MAXSIZE];
int top; /* 用于栈顶指针 */
}SqStack;
1、栈的顺序存储结构——进栈操作
进栈操作即栈顶指针加一,将新元素值赋给栈顶空间(push):
/* 插入元素e为新的栈顶元素 */
Status Push(SqStack *S,SElemType e)
{
if(S->top == MAXSIZE -1) /* 栈满 */
{
return ERROR;
}
S->top++; /* 栈顶指针增加一 */
S->data[S->top]=e; /* 将新插入元素赋值给栈顶空间 */
return OK;
}
2、栈的顺序存储结构——出栈操作
出栈操作删除栈顶元素,栈顶指针减一(pop):
/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */
Status Pop(SqStack *S,SElemType *e)
{
if(S->top==-1)
return ERROR;
*e=S->data[S->top]; /* 将要删除的栈顶元素赋值给e */
S->top--; /* 栈顶指针减一 */
return OK;
}
上述操作时间复杂度均为O(1)。
(四)两栈共享空间
利用一个数组来存储两个栈,数组的两个端点分别为两个栈的栈底,两个栈如果增加元素,就是两个端点向中间延伸。

两栈共享空间的结构:
// 两栈共享结构
typedef struct {
ElemType data[MAXSIZE]; // 用于存储元素值
int top1; // 用于指示栈1的栈顶指针
int top2; // 用于指示栈2的栈顶指针
}SqStack;
两栈共享空间的push方法:
// 插入元素e为新的栈顶元素
Status Push(SqStack *S, ElemType e, int stackNumber)
{
if (S->top1 + 1 == S->top2) // 栈满时,添加失败
{
return ERROR;
}
// 给栈1添加新元素
if (stackNumber == 1)
S->data[++S->top1] = e; // 将新元素添加到栈1的栈顶
else // 给栈2添加新元素
S->data[--S->top2] = e; // 将新元素添加到栈2的栈顶
return OK;
}
两栈共享空间的pop方法:
// 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK,否则返回ERROR
Status Pop(SqStack *S, ElemType *e, int stackNumber)
{
// 栈1弹出元素
if (stackNumber == 1) {
if (S->top1 == -1) // 栈为空时,弹出元素失败
return ERROR;
*e = S->data[S->top1--]; // 将栈顶元素的值赋给e元素,栈1的栈顶指针减1
}
else // 栈2弹出元素
{
if (S->top2 == MAXSIZE)
return ERROR;
*e = S->data[S->top2++]; // 将栈顶元素的值赋给e元素,栈2的栈顶指针加1
}
return OK;
}
了解下就好使用这样的数据结构,通常是当两个栈的空间需求具有相反关系时才有意义且需要两个具有相同数据类型的栈才可以。
(五)栈的链式存储结构及实现
栈的链式存储结构,简称为链栈。对于链栈来说是不需要头结点的因为栈顶指针可代替头结点作用,而且链栈不存在栈满的情况,如果是空栈,就是top = NULL。

链式结构如下:
/* 链栈结构 */
typedef struct StackNode
{
SElemType data;
struct StackNode *next;
}StackNode,*LinkStackPtr;
typedef struct LinkStack
{
LinkStackPtr top;
int count;
}LinkStack;
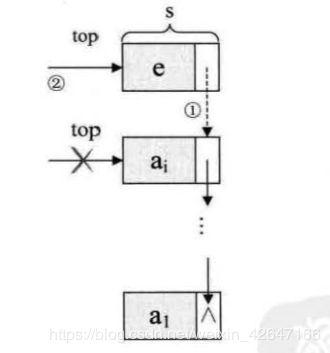
1、栈的链式存储结构——进栈操作
/* 插入元素e为新的栈顶元素 */
Status Push(LinkStack *S,SElemType e)
{
LinkStackPtr s=(LinkStackPtr)malloc(sizeof(StackNode));
s->data=e;
s->next=S->top; /* 把当前的栈顶元素赋值给新结点的直接后继,见图中① */
S->top=s; /* 将新的结点s赋值给栈顶指针,见图中② */
S->count++;
return OK;
}
2、栈的链式存储结构——出栈操作
/* 若栈不空,则删除S的栈顶元素,用e返回其值,并返回OK;否则返回ERROR */
Status Pop(LinkStack *S,SElemType *e)
{
LinkStackPtr p;
if(StackEmpty(*S))
return ERROR;
*e=S->top->data;
p=S->top; /* 将栈顶结点赋值给p,见图中③ */
S->top=S->top->next; /* 使得栈顶指针下移一位,指向后一结点,见图中④ */
free(p); /* 释放结点p */
S->count--;
return OK;
}
上述时间复杂度也均为O(1),如过栈的使用过程中元素变化不可预料,最好用链栈;如果变化在可控范围内,则用顺序栈好些。
(六)队列的定义
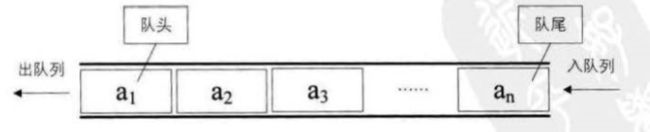
队列 ( queue ) 是只允许在一端进行插入操作,而在另一端进行删除操作的线性表。,队列是一种先进先出(First In First Out)的线性表,简称FIFO。允许插入的一段称为队尾,允许删除的一端称为队头。
(七)队列的基本操作
ADT 队列 (Queue)
Data
同线性表。元素具有相同的类型,相邻元素具有前驱和后继关系 。
Operation
InitQueue(*Q) :初始化操作,建立一个空队列Q。
DestroyQueue(*Q) :若队列Q存在,则销毁它。
ClearQueue(*Q) :将队列Q清空。
QueueEmpty(Q) :若队列Q为空,返回true,否则返回false。
GetHead(Q,*e) :若队列Q存在且非空,用e返回队列Q的队头元素。
EnQueue(*Q,e) :若队列Q存在,插入新元素e到队列Q中并成为对尾元素 。
DeQueue(*Q,*e) :删除队列Q中队头元素,并用e返回其值。
QueueLength(Q) :返回队列Q的元素个数
endADT
(八)循环队列
1、顺序队列的不足
假设我们有一个队列里面有n个元素,入队列操作就是在队尾加入一个新元素,不移动其他元素,其时间复杂度为O(1)。

因为队列是先进先出,而出队操作时队头出队的时候队列中其他元素都要向前移动,其时间复杂度为O(n)。
为了解决出队操作的麻烦引入了两个指针:front 指针指向队头元素,rear 指针指向队尾元素的下一个元素。当front = rear时队列为空。

这样虽然解决一定问题但是如果队列经过出队操作后我队列前是空闲的,其队尾元素已被占用(rear)移动到数组外。如下图所示:

这样的情况叫做“假溢出”。因此可看出顺序队列有很多的问题,因此我们引入了新的结构——循环队列。
2、顺序队列定义及操作
我们把队列头尾相接的顺序存储结构叫做循环队列。例如刚才rear指针指向数组外的情况,我们可将他重新指到队列头未被占用的空间,就可解决问题。

此种情况我们需要讨论的问题队列何时为满队列:假设队列最大尺寸为QueueSize,队列满的条件为 (rear+1)%QueueSize == front(取模是为了整合rear与front大小),计算队列长度公式为 (rear - front + QueueSize)% QueueSize。
循环队列顺序存储结构如下:
/* 循环队列的顺序存储结构 */
typedef int QElemType; /* QElemType类型根据实际情况而定,这里假设为int */
typedef struct
{
QElemType data[MAXSIZE];
int front; /* 头指针 */
int rear; /* 尾指针,若队列不空,指向队列尾元素的下一个位置 */
}SqQueue;
循环队列初始化:
/* 初始化一个空队列Q */
Status InitQueue(SqQueue *Q)
{
Q->front=0;
Q->rear=0;
return OK;
}
循环队列入队操作:
/* 若队列未满,则插入元素e为Q新的队尾元素 */
Status EnQueue(SqQueue *Q,QElemType e)
{
if ((Q->rear+1)%MAXSIZE == Q->front) /* 队列满的判断 */
return ERROR;
Q->data[Q->rear]=e; /* 将元素e赋值给队尾 */
Q->rear=(Q->rear+1)%MAXSIZE;/* rear指针向后移一位置, */
/* 若到最后则转到数组头部 */
return OK;
}
循环队列出队操作:
/* 若队列不空,则删除Q中队头元素,用e返回其值 */
Status DeQueue(SqQueue *Q,QElemType *e)
{
if (Q->front == Q->rear) /* 队列空的判断 */
return ERROR;
*e=Q->data[Q->front]; /* 将队头元素赋值给e */
Q->front=(Q->front+1)%MAXSIZE; /* front指针向后移一位置, */
/* 若到最后则转到数组头部 */
return OK;
}
(九)队列的链式存储及实现
队列的链式存储结构,其实就是线性表的单链表,只不过是尾进头出,我们把它叫做链队列。
链队列结构:
typedef int QElemType; /* QElemType类型根据实际情况而定,这里假设为int */
typedef struct QNode /* 结点结构 */
{
QElemType data;
struct QNode *next;
}QNode,*QueuePtr;
typedef struct /* 队列的链表结构 */
{
QueuePtr front,rear; /* 队头、队尾指针 */
}LinkQueue;
链队列入队操作:
/* 插入元素e为Q的新的队尾元素 */
Status EnQueue(LinkQueue *Q,QElemType e)
{
QueuePtr s=(QueuePtr)malloc(sizeof(QNode));
if(!s) /* 存储分配失败 */
exit(OVERFLOW);
s->data=e;
s->next=NULL;
Q->rear->next=s; /* 把拥有元素e的新结点s赋值给原队尾结点的后继,见图中① */
Q->rear=s; /* 把当前的s设置为队尾结点,rear指向s*/
return OK;
}
链队列出队操作:
/* 若队列不空,删除Q的队头元素,用e返回其值,并返回OK,否则返回ERROR */
Status DeQueue(LinkQueue *Q,QElemType *e)
{
QueuePtr p;
if(Q->front==Q->rear)
return ERROR;
p=Q->front->next; /* 将欲删除的队头结点暂存给p,见图中① */
*e=p->data; /* 将欲删除的队头结点的值赋值给e */
Q->front->next=p->next;/* 将原队头结点的后继p->next赋值给头结点后继,见图中② */
if(Q->rear==p) /* 若队头就是队尾,则删除后将rear指向头结点*/
Q->rear=Q->front;
free(p);
return OK;
}
参考书籍:《大话数据结构》