自然语言处理入门练习（三）：基于注意力机制的文本匹配（附代码）

自然语言处理入门练习（三）：基于注意力机制的文本匹配（附代码）

一、注意力机制

1 认知神经学中的注意力

  注意力（Attention）：人脑可以有意或无意地从这些大量输入信息中选择小部分的有用信息来重点处理，并忽略其他信息。
  注意力一般分为两种：
  （1）自上而下的有意识的注意力，称为聚焦式注意力（Focus Attention）。聚焦式注意力是指有预定目的、依赖任务的，主动有意识地聚焦于某一对象的注意力。
  （2）自下而上的无意识的注意力，称为基于显著性的注意力（Saliency Based Attention）。基于显著性的注意力是由外界刺激驱动的注意，不需要主动干预，也和任务无关。如果一个对象的刺激信息不同于其周围信息，一种无意识的“赢者通吃”（Winner-Take-All）或者门控（Gating）机制就可以把注意力转向这个对象。不管这些注意力是有意还是无意，大部分的人脑活动都需要依赖注意力，比如记忆信息、阅读或思考等。

2 注意力机制

  注意力机制（AttentionMechanism）作为一种资源分配方案，将有限的计算资源用来处理更重要的信息，是解决信息超载问题的主要手段。
  用=[1,⋯,]∈ℝ×表示组输入信息，其中维向量∈ℝ,∈[1,]表示一组输入信息。
  注意力机制的计算可以分为两步：一是在所有输入信息上计算注意力分布，二是根据注意力分布来计算输入信息的加权平均。
  注意力分布为了从个输入向量[1,⋯,]中选择出和某个特定任务相关的信息，我们需要引入一个和任务相关的表示，称为查询向量（QueryVector），并通过一个打分函数来计算每个输入向量和查询向量之间的相关性。
  给定一个和任务相关的查询向量，我们用注意力变量∈[1,]来表示被选择信息的索引位置，即=表示选择了第个输入向量。为了方便计算，我们采用一种“软性”的信息选择机制。首先计算在给定和下，选择第个输入向量的概率，

其中称为注意力分布（AttentionDistribution），(,)为注意力打分函数，可以使用以下几种方式来计算：

其中,,为可学习的参数，为输入向量的维度。
  加权平均注意力分布可以解释为在给定任务相关的查询时，第个输入向量受关注的程度。我们采用一种“软性”的信息选择机制对输入信息进行汇总，即

  公式(8.7)称为软性注意力机制（SoftAttentionMechanism）。图8.1a给出软性注意力机制的示例。

2.1注意力机制的变体

  除了上面介绍的基本模式外，注意力机制还存在一些变化的模型。

2.1.1硬性注意力

  公式(8.7)提到的注意力是软性注意力，其选择的信息是所有输入向量在注意力分布下的期望。此外，还有一种注意力是只关注某一个输入向量，叫作硬性注意力（HardAttention）。
  硬性注意力有两种实现方式：
  （1）一种是选取最高概率的一个输入向量，即

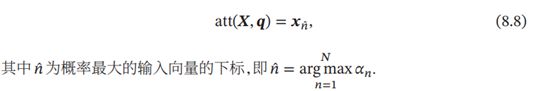
  （2）另一种硬性注意力可以通过在注意力分布式上随机采样的方式实现。

2.1.2键值对注意力

  更一般地，我们可以用键值对（key-valuepair）格式来表示输入信息，其中“键”用来计算注意力分布，“值”用来计算聚合信息。
  用(,)=[(1,1),⋯,(,)]表示组输入信息，给定任务相关的查询向量时，注意力函数为

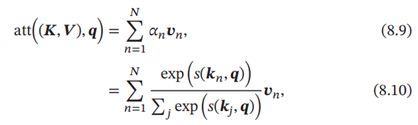
其中(,)为打分函数。

2.1.3多头注意力

  多头注意力（Multi-HeadAttention）是利用多个查询=[1,⋯,]，来并行地从输入信息中选取多组信息。每个注意力关注输入信息的不同部分。

其中⊕表示向量拼接。

2.1.4结构化注意力

  在之前介绍中，我们假设所有的输入信息是同等重要的，是一种扁平（Flat）结构，注意力分布实际上是在所有输入信息上的多项分布。但如果输入信息本身具有层次（Hierarchical）结构，比如文本可以分为词、句子、段落、篇章等不同粒度的层次，我们可以使用层次化的注意力来进行更好的信息选择[Yangetal.,2016]。此外，还可以假设注意力为上下文相关的二项分布，用一种图模型来构建更复杂的结构化注意力分布[Kimetal.,2017]。

2.1.5指针网络

  注意力机制主要是用来做信息筛选，从输入信息中选取相关的信息。注意力机制可以分为两步：一是计算注意力分布，二是根据来计算输入信息的加权平均。我们可以只利用注意力机制中的第一步，将注意力分布作为一个软性的指针（pointer）来指出相关信息的位置。
  指针网络（PointerNetwork）[Vinyalsetal.,2015]是一种序列到序列模型，输入是长度为的向量序列=1,⋯,，输出是长度为的下标序列1∶=1,2,⋯,，∈[1,],∀。
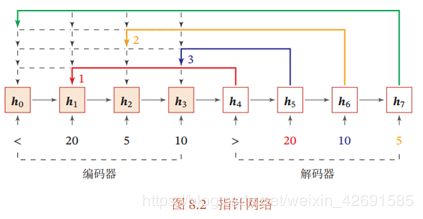
  和一般的序列到序列任务不同，这里的输出序列是输入序列的下标（索引）。比如输入一组乱序的数字，输出为按大小排序的输入数字序列的下标。比如输入为20,5,10，输出为1,3,2。条件概率(1∶|1∶)可以写为

其中条件概率(|1,⋯,(-1),1∶)可以通过注意力分布来计算。假设用一个循环神经网络对1,⋯,-1,1∶进行编码得到向量，则

其中,为在解码过程的第步时，对的未归一化的注意力分布，即

其中,,为可学习的参数。
  图8.2给出了指针网络的示例，其中1,2,3为输入数字20,5,10经过循环神经网络的隐状态，0对应一个特殊字符‘<’。当输入‘>’时，网络一步一步输出三个输入数字从大到小排列的下标。

3 自注意力模型

  当使用神经网络来处理一个变长的向量序列时， 我们通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列， 如图8.3所示。

  基于卷积或循环网络的序列编码都是一种局部的编码方式，只建模了输入信息的局部依赖关系。虽然循环网络理论上可以建立长距离依赖关系，但是由于信息传递的容量以及梯度消失问题，实际上也只能建立短距离依赖关系。
  如果要建立输入序列之间的长距离依赖关系，可以使用以下两种方法：一种方法是增加网络的层数，通过一个深层网络来获取远距离的信息交互；另一种方法是使用全连接网络。全连接网络是一种非常直接的建模远距离依赖的模型， 但是无法处理变长的输入序列。 不同的输入长度， 其连接权重的大小也是不同的。这时我们就可以利用注意力机制来“动态” 地生成不同连接的权重，这就是自注意力模型（ Self-Attention Model）。
  为了提高模型能力，自注意力模型经常采用查询-键-值（ Query-Key-Value，QKV）模式， 其计算过程如图8.4所示，其中红色字母表示矩阵的维度。

  假设输入序列为 = [1, ⋯ , ] ∈ ℝ× ，输出序列为 = [1, ⋯ , ] ∈ℝ× ，自注意力模型的具体计算过程如下：
  （ 1） 对于每个输入，我们首先将其线性映射到三个不同的空间，得到查询向量 ∈ ℝ 、键向量 ∈ ℝ 和值向量 ∈ ℝ 。
对于整个输入序列，线性映射过程可以简写为

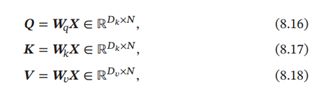
其中 ∈ ℝ×, ∈ ℝ×, ∈ ℝ× 分别为线性映射的参数矩阵， = [1, ⋯ , ], = [1, ⋯ , ], = [1, ⋯ , ] 分别是由查询向量、 键向量和值向量构成的矩阵。
  （ 2） 对于每一个查询向量 ∈ ，利用公式(8.9)的键值对注意力机制，可以得到输出向量，

其中, ∈ [1, ]为输出和输入向量序列的位置， 表示第个输出关注到第个输入的权重。
  如果使用缩放点积来作为注意力打分函数，输出向量序列可以简写为

其中softmax(⋅)为按列进行归一化的函数。
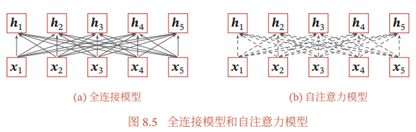
  图8.5给出全连接模型和自注意力模型的对比，其中实线表示可学习的权重，虚线表示动态生成的权重。由于自注意力模型的权重是动态生成的，因此可以处理变长的信息序列。

  自注意力模型可以作为神经网络中的一层来使用，既可以用来替换卷积层和循环层 [Vaswani et al., 2017]，也可以和它们一起交替使用（ 比如 可以是卷积层或循环层的输出）。自注意力模型计算的权重 只依赖于 和 的相关性，而忽略了输入信息的位置信息。因此在单独使用时， 自注意力模型一般需要加入位置编码信息来进行修正 [Vaswani et al., 2017]。 自注意力模型可以扩展为多头自注意力（ Multi-Head Self-Attention） 模型，在多个不同的投影空间中捕捉不同的交互信息。

二、文本匹配

1、文本匹配基本概念

  文本匹配是自然语言处理中一个重要的基础问题，可以应用于大量的NLP任务中，如信息检索、问答系统、复述问题、对话系统、机器翻译等，这些NLP任务在很大程度上可以抽象为文本匹配问题。
  例如网页搜索可抽象为网页同用户搜索Query的一个相关性匹配问题，自动问答可抽象为候选答案与问题的满足度匹配问题，文本去重可以抽象为文本与文本的相似度匹配问题。

2、文本匹配任务

  在真实场景中，如搜索引擎、智能问答、知识检索、信息流推荐等系统中的召回、排序环节，通常面临的是如下任务：
从大量存储的 doc 中，选取与用户输入 query 最匹配的那个 doc。

• 在搜索引擎中，“doc”对应索引网页的相关信息，如 title、content 等，“query”对应用户的检索请求，“最匹配”对应（点击行为）相关度最高。
• 在智能问答中，“doc”对应 FAQ 中的 question，“query”对应用户的问题，“最匹配”对应语义相似度最高。
• 在信息流推荐中，“doc”对应待推荐的 feed 流，“query”对应用户的画像，“最匹配”对应用户最感兴趣等众多度量标准。

  解决这些任务，无监督和有监督学习都提供了一些具体方法，我们这里先谈论有监督学习。通常，这些任务的训练样本具有同样的结构：
   共 N 组数据，每组数据结构相同：1 个 query，对应的 M 个 doc，对应的 M 个标签。

• 在搜索引擎中，query 会被表征为包含文本语义和用户信息的 embedding，doc 会被表征为包含索引网页各项信息的 embedding
• 在智能问答中，query 会被表征为以文本语义为主的 embedding，doc 同样表征为以文本语义为主的 embedding
• 在信息流推荐中，query 会被表征为包含文本特征各项信息的 embedding，doc 会被表征为包含用户历史、爱好等信息的 embedding

  可见，query 和 doc 的表征形式较固定，至于具体 embedding 包含的信息根据具体任务、场景、目标变化极大，按需设计。
但至于训练样本中的标签，形式则区别甚大。可以分成下述三种形式：

• pointwise，M 通常为 1，标签形式为 0 或 1，标签 0 表示 query 与该 doc 不匹配，标签 1 表示匹配。M 也可大于 1 ，此时，一组数据中只有一个 1 其余全为 0，表示这 M 个 doc 中只有这一个与 query 匹配，其余全都不匹配。
• pairwise，M 通常为 2，标签形式为 0 或 1 ，标签 0 表示 query 与第一个 doc 比与第二个 doc 更匹配，标签 1 表示 query 与第二个 doc 比与第一个 doc 更匹配，当然也可以反之。
• listwise，M 通常大于等于 2，标签形式为 1 到 M 的正整数，标签 m 表示 query 与该 doc 的匹配度在该组里位列第 m 位。

  上述三种不同监督形式，形成了不同的学习方式，彼此之间优劣异同就涉及到 Learning2Rank 技术了，具体可参考之前的博文，这里不再赘述。虽然越靠后的形式得到的模型越符合我们预期，但其对训练样本形式的严苛性和算法设计的复杂性使得工业应用难以开展，通常，解决我们遇到的任务，多采用 pointwise 或者 pairwise 方式。

  再回顾下 “从大量存储的 doc 中，选取与用户输入 query 最匹配的那个 doc” 这个经典问题，doc 与 query 的具体指代的改变使之可以推广到多个具体任务中，监督信息则可以从两个维度拓展：

• 监督信号的含义，决定了 doc 与 query 匹配的准则。如在智能问答、知识检索中，doc 与 query 形式基本一致，标注时，如果根据文本语义相似度对 doc 与 query 打标签，那自然最终学习到的模型就是语义相似度模型，如果根据检索后点击行为对 doc 与 query 打标签，那自然最终学习到的模型就是行为相关性模型。
• 监督信号的标注形式，决定了其可采纳的学习形式。通常，按 listwise、pairwise、pointwise 顺序，形式可以退化，即由 listwise 形式的数据构造出 pointwise 形式的数据，也可以引入其他信息后，按逆序进行升格，即由 pointwise 形式的数据构造出 listwise 形式的数据。

  这一节，我们尽量将问题泛化，将多个相关任务进行了关联。那么，下面将就具体的任务 —— 文本语义相似度计算 —— 进行介绍。

3、文本语义相似度计算

  PI、SSEI、STS、IR-QA、Ad-hoc retrieval
  谈起相似度计算，经常会出现几个关联的 NLP 任务，彼此存在微妙的区别：

• paraphrase identification，即 PI，是判断一文本是否另一文本的复述
• semantic text similarity，即 STS，是计算两文本在语义层面的相似性
• sentence semantic equivalent identification，即 SSEI，是判断两文本在语义层面是否一致
• IR-QA，是给定一个 query，直接从一堆 answer 中寻找最匹配的，省略了 FAQ 中 question-answer pair 的 question 中转
• Ad-hoc retrieval，属于典型的相关匹配问题

  当然，如何定义“相似”也是个开放问题。
  Quora 曾尝试从更实用的角度给出定义，如果多个 query 所反映的意图一致，或者说可以用同一个 answer 回答，则可以认为语义一致，即 SSEI。这也更符合 FAQ 问答系统中文本语义相似度计算的诉求。
  此外，需要注意的是，虽然定义有区别，但几个任务基于神经网络提出的很多模型，是彼此通用的。许多经典模型在一个任务上被提出，评估时都会在其他几个任务的数据上跑一下。当然，一个模型迁移到其他任务时，也会进行针对性的微调，后面也会介绍到。总之，应该多关注这几个相关任务上的技术发展，借鉴引用。

3.1 常用数据集

• PI、SSEI、STS 英文：MSRP、SICK、SNLI、STS、Quora QP、MultiNLI
• PI、SSEI、STS 中文：LCQMC、BQ corpus
• IR-QA 英文：wikiQA、insuranceQA

3.2 无监督技术

  不少经典的无监督 STS 技术，虽然简朴，但也能取得不错的效果：

• 基于词汇重合度：TFIDF、VSM、LD、LCS、BM25、Jaccord、SimHash 等
• 基于浅层语义的主题模型：LSA、pLSA、LDA 等
• 基于浅层语义的 encoding 模型：embedding centroid、WMD、InferSent、pretrained encoder 等

  虽然无监督技术较粗糙，但能有效解决冷启动问题。如 Solr 全文检索引擎就在用基于 Ngram LD 的相似度召回技术，FAQ 问答引擎中使用 BOW+LD 也能取得不错的效果。主题模型和基于词向量的模型，本质上都是基于词共现信息的，虽然引入了词义信息，但实际使用中，并无法替代基于词汇重合度的经典算法，效果相差不大。
  基于有监督的相似度计算，我们主要介绍基于神经网络的，基本可以分为两大类，sentence encoding (sentence representation) 类、sentence interaction 类。

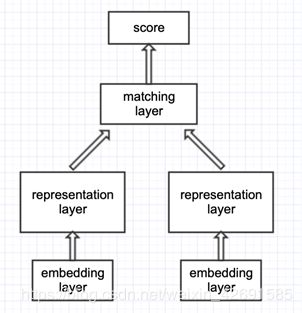
3.3 SE 网络

  SE 网络结构如下：

• representation-based 类模型，思路是基于 Siamese 网络，提取文本整体语义再进行匹配
• 典型的 Siamese 结构，双塔共享参数，将两文本映射到同一空间，才具有匹配意义
• 表征层进行编码，使用 MLP、CNN、RNN、Self-attention、Transformer encoder、BERT 均可
• 匹配层进行交互计算，采用点积、余弦、高斯距离、MLP、相似度矩阵均可
• 经典模型有：DSSM、CDSSM、MV-LSTM、ARC-I、CNTN、CA-RNN、MultiGranCNN 等
• 优点是可以对文本预处理，构建索引，大幅降低在线计算耗时
• 缺点是失去语义焦点，易语义漂移，难以衡量词的上下文重要性

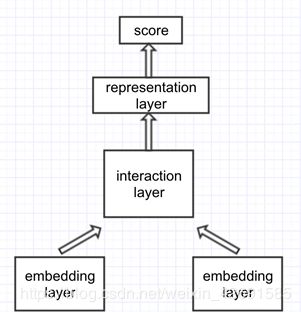
3.4 SI 网络

  SI 网络结构如下：

• interaction-based 类模型，思路是捕捉直接的匹配信号（模式），将词间的匹配信号作为灰度图，再进行后续建模抽象
• 交互层，由两文本词与词构成交互矩阵，交互运算类似于 attention，加性乘性都可以
• 表征层，负责对交互矩阵进行抽象表征，CNN、S-RNN 均可
• 经典模型有：ARC-II、MatchPyramid、Match-SRNN、K-NRM、DRMM、DeepRank、DUET、IR-Transformer、DeepMatch、ESIM、ABCNN、BIMPM 等
• 优点是更好地把握了语义焦点，能对上下文重要性进行更好的建模
• 缺点是忽视了句法、句间对照等全局性信息，无法由局部匹配信息刻画全局匹配信息

【实战任务】

  输入两个句子判断，判断它们之间的关系。参考ESIM（可以只用LSTM，忽略Tree-LSTM），用双向的注意力机制实现。

【核心代码】

import torch

from torch import nn

class VariationalDropout(nn.Dropout):
    """
    Apply the dropout technique in Gal and Ghahramani, "Dropout as a Bayesian Approximation:
    Representing Model Uncertainty in Deep Learning" (https://arxiv.org/abs/1506.02142) to a
    3D tensor.
    This module accepts a 3D tensor of shape ``(batch_size, num_timesteps, embedding_dim)``
    and samples a single dropout mask of shape ``(batch_size, embedding_dim)`` and applies
    it to every time step.
    """
    def forward(self, input_tensor):
        """
        Apply dropout to input tensor.
        Parameters
        ----------
        input_tensor: ``torch.FloatTensor``
            A tensor of shape ``(batch_size, num_timesteps, embedding_dim)``
        Returns
        -------
        output: ``torch.FloatTensor``
            A tensor of shape ``(batch_size, num_timesteps, embedding_dim)`` with dropout applied.
        """
        ones = input_tensor.data.new_ones(input_tensor.shape[0], input_tensor.shape[-1])
        dropout_mask = torch.nn.functional.dropout(ones, self.p, self.training, inplace=False)
        if self.inplace:
            input_tensor *= dropout_mask.unsqueeze(1)
            return None
        else:
            return dropout_mask.unsqueeze(1) * input_tensor

class EmbeddingLayer(nn.Module):
    """Implement embedding layer.
    """
    def __init__(self, vector_size, vocab_size, dropout=0.5):
        """
        Arguments:
            vector_size {int} -- word embedding size.
            vocab_size {int} -- vocabulary size.
        Keyword Arguments:
            dropout {float} -- dropout rate. (default: {0.5})
        """
        super(EmbeddingLayer, self).__init__()

        self.vector_size = vector_size
        self.embed = nn.Embedding(vocab_size, vector_size)
        self.dropout = VariationalDropout(dropout)

    def load(self, vectors):
        """Load pre-trained embedding weights.
        Arguments:
            vectors {torch.Tensor} -- from "TEXT.vocab.vectors".
        """
        self.embed.weight.data.copy_(vectors)

    def forward(self, x):
        """
        Arguments:
            x {torch.Tensor} -- input tensor with shape [batch_size, seq_length]
        """
        e = self.embed(x)
        return self.dropout(e)

class EncodingLayer(nn.Module):
    """BiLSTM encoder which encodes both the premise and hypothesis.
    """
    def __init__(self, input_size, hidden_size):
        super(EncodingLayer, self).__init__()
        self.lstm = nn.LSTM(input_size, hidden_size,
                            num_layers=1,
                            bidirectional=True)

    def forward(self, x):
        """
        Arguments:
            x {torch.Tensor} -- input embeddings with shape [batch, seq_len, input_size]
        Returns:
            output {torch.Tensor} -- [batch, seq_len, num_directions * hidden_size]
        """
        self.lstm.flatten_parameters()
        output, _ = self.lstm(x)
        return output

class LocalInferenceModel(nn.Module):
    """The local inference model introduced in the paper.
    """
    def __init__(self):
        super(LocalInferenceModel, self).__init__()
        self.softmax_1 = nn.Softmax(dim=1)
        self.softmax_2 = nn.Softmax(dim=2)

    def forward(self, p, h, p_mask, h_mask):
        """Apply local inference to premise and hyopthesis.
        Arguments:
            p {torch.Tensor} -- p has shape [batch, seq_len_p, 2 * hidden_size]
            h {torch.Tensor} -- h has shape [batch, seq_len_h, 2 * hidden_size]
            p_mask {torch.Tensor (int)} -- p has shape [batch, seq_len_p], 0 in the mask
                means padding.
            h_mask {torch.Tensor (int)} -- h has shape [batch, seq_len_h]
        Returns:
            m_p, m_h {torch.Tensor} -- tensor with shape [batch, seq_len, 8 * hidden_size]
        """
        # equation 11 in the paper:
        e = torch.matmul(p, h.transpose(1, 2))  # [batch, seq_len_p, seq_len_h]

        # masking the scores for padding tokens
        inference_mask = torch.matmul(p_mask.unsqueeze(2).float(),
                                      h_mask.unsqueeze(1).float())
        e.masked_fill_(inference_mask < 1e-7, -1e7)

        # equation 12 & 13 in the paper:
        h_score, p_score = self.softmax_1(e), self.softmax_2(e)
        h_ = h_score.transpose(1, 2).bmm(p)
        p_ = p_score.bmm(h)

        # equation 14 & 15 in the paper:
        m_p = torch.cat((p, p_, p - p_, p * p_), dim=-1)
        m_h = torch.cat((h, h_, h - h_, h * h_), dim=-1)

        assert inference_mask.shape == e.shape
        assert p.shape == p_.shape and h.shape == h_.shape
        assert m_p.shape[-1] == p.shape[-1] * 4

        return m_p, m_h


class CompositionLayer(nn.Module):
    """The composition layer.
    """
    def __init__(self, input_size, output_size, hidden_size, dropout=0.5):
        """
        Arguments:
            input_size {int} -- input size to the feedforward neural network.
            output_size {int} -- output size of the feedforward neural network.
            hidden_size {int} -- output hidden size of the LSTM model.
        Keyword Arguments:
            dropout {float} -- dropout rate (default: {0.5})
        """
        super(CompositionLayer, self).__init__()
        self.hidden_size = hidden_size
        self.F = nn.Linear(input_size, output_size)
        self.lstm = nn.LSTM(output_size, hidden_size,
                            num_layers=1, bidirectional=True)
        self.dropout = VariationalDropout(dropout)

    def forward(self, m):
        """
        Arguments:
            m {torch.Tensor} -- [batch, seq_len, input_size]
        Returns:
            outputs {torch.Tensor} -- [batch, seq_len, hidden_size * 2]
        """
        y = self.dropout(self.F(m))
        self.lstm.flatten_parameters()
        outputs, _ = self.lstm(y)

        assert m.shape[:2] == outputs.shape[:2] and \
            outputs.shape[-1] == self.hidden_size * 2
        return outputs


class Pooling(nn.Module):
    """Apply maxing pooling and average pooling to the outputs of LSTM.
    """
    def __init__(self):
        super(Pooling, self).__init__()

    def forward(self, x, x_mask):
        """
        Arguments:
            x {torch.Tensor} -- [batch, seq_len, hidden_size * 2]
            x_mask {torch.Tensor} -- [batch, seq_len], 0 in the mask means padding
        Returns:
            v {torch.Tensor} -- [batch, hidden_size * 4]
        """
        mask_expand = x_mask.unsqueeze(-1).expand(x.shape)

        # average pooling
        x_ = x * mask_expand.float()
        v_avg = x_.sum(1) / x_mask.sum(-1).unsqueeze(-1).float()

        # max pooling
        x_ = x.masked_fill(mask_expand == 0, -1e7)
        v_max = x_.max(1)[0]

        assert v_avg.shape == v_max.shape == (x.shape[0], x.shape[-1])
        return torch.cat((v_avg, v_max), dim=-1)

class InferenceComposition(nn.Module):
    """Inference composition described in paper section 3.3
    """
    def __init__(self, input_size, output_size, hidden_size, dropout=0.5):
        """
        Arguments:
            input_size {int} -- input size to the feedforward neural network.
            output_size {int} -- output size of the feedforward neural network.
            hidden_size {int} -- output hidden size of the LSTM model.
        Keyword Arguments:
            dropout {float} -- dropout rate (default: {0.5})
        """
        super(InferenceComposition, self).__init__()
        self.composition = CompositionLayer(input_size,
                                            output_size,
                                            hidden_size,
                                            dropout=dropout)
        # self.composition_h = deepcopy(self.composition_p)
        self.pooling = Pooling()

    def forward(self, m_p, m_h, p_mask, h_mask):
        """
        Arguments:
            m_p {torch.Tensor} -- [batch, seq_len, input_size]
            m_h {torch.Tensor} -- [batch, seq_len, input_size]
            mask {torch.Tensor} -- [batch, seq_len], 0 means padding
        Returns:
            v {torch.Tensor} -- [batch, input_size * 8]
        """
        # equation 16 & 17 in the paper
        v_p, v_h = self.composition(m_p), self.composition(m_h)
        # equation 18 & 19 in the paper
        v_p_, v_h_ = self.pooling(v_p, p_mask), self.pooling(v_h, h_mask)
        # equation 20 in the paper
        v = torch.cat((v_p_, v_h_), dim=-1)

        assert v.shape == (m_p.shape[0], v_p.shape[-1] * 4)
        return v

class LinearSoftmax(nn.Module):
    """Implement the final linear layer.
    """
    def __init__(self, input_size, output_size, class_num, activation='relu', dropout=0.5):
        super(LinearSoftmax, self).__init__()
        if activation == 'relu':
            self.activation = nn.ReLU()
        elif activation == 'tanh':
            self.activation = nn.Tanh()
        else:
            raise ValueError("Unknown activation function!!!")
        self.dropout = nn.Dropout(dropout)

        self.mlp = nn.Sequential(
            self.dropout,
            nn.Linear(input_size, output_size),
            self.activation,
            # self.dropout,
            nn.Linear(output_size, class_num)
        )

    def forward(self, x):
        """
        Arguments:
            x {torch.Tensor} -- [batch, features]
        Returns:
            logits {torch.Tensor} -- raw, unnormalized scores for each class. [batch, class_num]
        """
        logits = self.mlp(x)
        return logits


class ESIM(nn.Module):
    """Implement ESIM model using the modules defined above.
    """

    def __init__(self,
                 hidden_size,
                 vector_size=64,
                 vocab_size = 1973,
                 num_labels=3,
                 dropout=0.5,
                 device='gpu'
                 ):
        """
        Arguments:
            vector_size {int} -- word embedding size.
            vocab_size {int} -- the size of the vocabulary.
            hidden_size {int} -- LSTM hidden size.

        Keyword Arguments:
            class_num {int} -- number of class for classification (default: {3})
            dropout {float} -- dropout rate (default: {0.5})
        """
        super(ESIM, self).__init__()
        self.device = device
        self.embedding_layer = EmbeddingLayer(vector_size, vocab_size, dropout)
        self.encoder = EncodingLayer(vector_size, hidden_size)
        # self.hypo_encoder = deepcopy(self.premise_encoder)
        self.inference = LocalInferenceModel()
        self.inferComp = InferenceComposition(hidden_size * 8,
                                              hidden_size,
                                              hidden_size,
                                              dropout)
        self.linear = LinearSoftmax(hidden_size * 8,
                                    hidden_size,
                                    num_labels,
                                    activation='tanh')

    def load_embeddings(self, vectors):
        """Load pre-trained word embeddings.
        Arguments:
            vectors {torch.Tensor} -- pre-trained vectors.
        """
        self.embedding_layer.load(vectors)

    def forward(self, p, p_length, h, h_length):
        """
        Arguments:
            p {torch.Tensor} -- premise [batch, seq_len]
            h {torch.Tensor} -- hypothesis [batch, seq_len]
        Returns:
            logits {torch.Tensor} -- raw, unnormalized scores for each class
                with shape [batch, class_num]
        """
        # input embedding
        p_embeded = self.embedding_layer(p)
        h_embeded = self.embedding_layer(h)

        p_ = self.encoder(p_embeded)
        h_ = self.encoder(h_embeded)

        # local inference
        p_mask, h_mask = (p != 1).long(), (h != 1).long()
        m_p, m_h = self.inference(p_, h_, p_mask, h_mask)

        # inference composition
        v = self.inferComp(m_p, m_h, p_mask, h_mask)

        # final multi-layer perceptron
        logits = self.linear(v)
        probabilities = nn.functional.softmax(logits, dim=-1)

        return logits,probabilities

【完整代码github地址】

https://github.com/chenlian-zhou/nlp/tree/master/nlp_induction_training/task3

【参考资料】

1. 邱锡鹏的《神经网络与深度学习》
2. 文本匹配（语义相似度/行为相关性）技术综述
3. 论文推荐：Enhanced LSTM for Natural Language Inference
4. https://github.com/FudanNLP/nlp-beginner