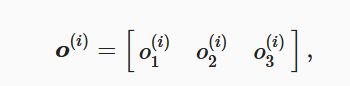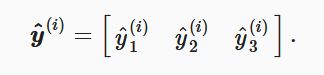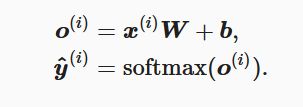softmax回归的原理及实现

1.softmax回归简介

softmax回归模型用于解决分类问题

首先考虑一个简单的图像分类问题，其输入图像的高和宽均为2像素，且色彩为灰度。这样每个像素值都可以用一个标量表示。我们将图像中的4像素分别记为x1,x2,x3,x4。假设训练数据集中图像的真实标签为狗、猫或鸡（假设可以用4像素表示出这3种动物），这些标签分别对应离散值y1,y2,y3，
我们通常使用离散的数值来表示类别，例如y1=1,y2=2,y3=3。

如此，一张图像的标签为1、2和3这3个数值中的一个。虽然我们仍然可以使用回归模型来进行建模，并将预测值就近定点化到1、2和3这3个离散值之一，但这种连续值到离散值的转化通常会影响到分类质量。因此我们一般使用更加适合离散值输出的模型来解决分类问题。

2.Fashion-mnist数据集下载及载入

Fashion-MNIST数据集是德国Zalando公司提供的衣物图像数据集，包含60,000个样本的训练 集和10,000个样本的测试集。每个样本都是 28x28灰度图像，与10个类别的标签相关联。Fashion-MNIST数据集旨在作为原始MNIST数据集的直接替代品，用于对机器学习算法进行基准测试。

数据集下载地址：
链接：https://pan.baidu.com/s/1UsygNeV6QJF9pTDP1N6nKg
提取码：1nk3

导入数据集：

def load_data_fashion_mnist(batch_size,resize=None,root='E:\FashionMNIST'):
    X_train, y_train = data_load('E:\FashionMNIST','train')
    X_test, y_test = data_load('E:\FashionMNIST','t10k')
    X_train_tensor = torch.from_numpy(X_train).to(torch.float32).view(-1,1,28,28)*(1/255)
    X_test_tensor = torch.from_numpy(X_test).to(torch.float32).view(-1,1,28,28)*(1/255)
    y_train_tensor = torch.from_numpy(y_train).to(torch.float32).view(-1,1)
    y_test_tensor = torch.from_numpy(y_test).to(torch.float32).view(-1,1)

    mnist_train = torch.utils.data.TensorDataset(X_train_tensor, y_train_tensor) 
    mnist_test = torch.utils.data.TensorDataset(X_test_tensor, y_test_tensor)

    if sys.platform.startswith('win'):
        num_workers=0
    else:
        num_workers=4

    train_iter=torch.utils.data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=num_workers)  
    test_iter=torch.utils.data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=num_workers)

    return train_iter,test_iter

3.softmax回归的理论推导过程

3.1softmax回归模型概述

softmax回归跟线性回归一样将输入特征与权重做线性叠加。与线性回归的一个主要不同在于，softmax回归的输出值个数等于标签里的类别数。因为一共有4种特征和3种输出动物类别，所以权重包含12个标量（带下标的w）、偏差包含3个标量（带下标的b），且对每个输入计算o1,o2,o3
这3个输出：

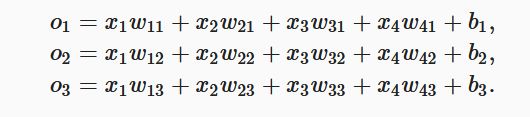
softmax回归同线性回归一样，也是一个单层神经网络。由于每个输出o1,o2,o3的计算都要依赖于所有的输入x1,x2,x3,x4，softmax回归的输出层也是一个全连接层。

3.2softmax运算

softmax运算符（softmax operator）通过下式将输出值变换成值为正且和为1的概率分布：

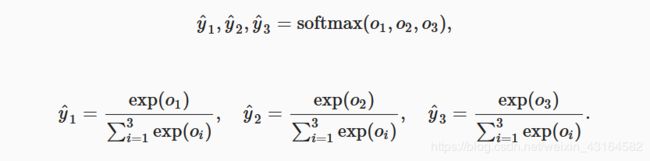
容易看出y^1 +y^2 +y^3 =1且0≤y^1 ,y^2 ,y^3 ≤1，因此y^1, y^2 ,y^3是一个合法的概率分布。

3.3单个样本的矢量计算

为了提高计算效率，我们可以将单样本分类通过矢量计算来表达。在上面的图像分类问题中，假设softmax回归的权重和偏差参数分别为

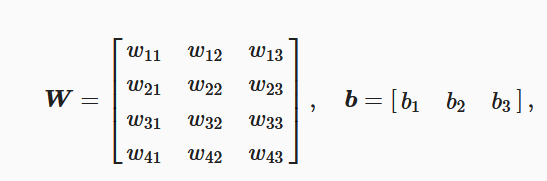
设高和宽分别为2个像素的图像样本i的特征为：

输出层的输出为：

预测为狗、猫或鸡的概率分布为：

softmax回归对样本i分类的矢量计算表达式为：

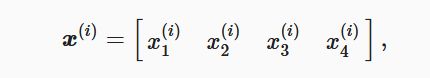
3.4小批量样本分类的矢量计算

3.5交叉熵损失函数

交叉熵（cross entropy）：

3.6模型评估

在训练好softmax回归模型后，给定任一样本特征，就可以预测每个输出类别的概率。通常，我们把预测概率最大的类别作为输出类别。如果它与真实类别（标签）一致，说明这次预测是正确的。

使用准确率（accuracy）来评价模型的表现。它等于正确预测数量与总预测数量之比。

4.softmax回归的代码实现（pytorch版本)`

#author：Simon
#data：2020.5.6

import torch
import torchvision
import numpy as np
import sys
import os
from torch import nn
import gzip
from torch.nn import init

#获取数据
def data_load(path, kind):
    images_path = os.path.join(path,'%s-images-idx3-ubyte.gz' % kind)
    labels_path = os.path.join(path,'%s-labels-idx1-ubyte.gz' % kind)
    with gzip.open(labels_path,'rb') as lbpath:
        labels = np.frombuffer(lbpath.read(),dtype=np.uint8, offset=8)    
    with gzip.open(images_path,'rb') as impath:
        images = np.frombuffer(impath.read(),dtype=np.uint8, offset=16).reshape(len(labels),784)
    return images, labels
    
#读取小批量数据
def load_data_fashion_mnist(batch_size,resize=None,root='E:\FashionMNIST'):
    X_train, y_train = data_load('E:\FashionMNIST','train')
    X_test, y_test = data_load('E:\FashionMNIST','t10k')
    X_train_tensor = torch.from_numpy(X_train).to(torch.float32).view(-1,1,28,28)*(1/255)
    X_test_tensor = torch.from_numpy(X_test).to(torch.float32).view(-1,1,28,28)*(1/255)
    y_train_tensor = torch.from_numpy(y_train).to(torch.float32).view(-1,1)
    y_test_tensor = torch.from_numpy(y_test).to(torch.float32).view(-1,1)

    mnist_train = torch.utils.data.TensorDataset(X_train_tensor, y_train_tensor) 
    mnist_test = torch.utils.data.TensorDataset(X_test_tensor, y_test_tensor)

    if sys.platform.startswith('win'):
        num_workers=0
    else:
        num_workers=4

    train_iter=torch.utils.data.DataLoader(mnist_train,batch_size=batch_size,shuffle=True,num_workers=num_workers)  
    test_iter=torch.utils.data.DataLoader(mnist_test,batch_size=batch_size,shuffle=True,num_workers=num_workers)

    return train_iter,test_iter

batch_size=100
train_iter,test_iter=load_data_fashion_mnist(batch_size)

print(len(train_iter),len(test_iter))

#定义和初始化模型
num_inputs=784
num_outputs=10

class LinearNet(nn.Module):
    def __init__(self, num_inputs, num_outputs):
        super(LinearNet, self).__init__()
        self.linear = nn.Linear(num_inputs, num_outputs)
    def forward(self, x): 
        y = self.linear(x.view(x.shape[0], -1))
        return y

net = LinearNet(num_inputs, num_outputs)

init.normal_(net.linear.weight,mean=0,std=0.01)       #初始化模型参数
init.constant_(net.linear.bias,val=0)

#softmax和交叉熵损失函数
loss=nn.CrossEntropyLoss()

#定义优化算法
optimizer=torch.optim.SGD(net.parameters(),lr=0.1)

#定义准确率
def evaluate_accuracy(data_iter, net):
    acc_sum, n = 0.0, 0
    for X, y in data_iter:
        y=y.numpy()
        y=y.flatten()
        y=torch.tensor(y)
        acc_sum += (net(X).argmax(dim=1) == y.long()).float().sum().item()
        n += y.shape[0]
    return acc_sum / n

#训练模型
num_epochs=10
def train(net, train_iter, test_iter, loss, num_epochs, batch_size,params=None, lr=None, optimizer=optimizer):
    for epoch in range(num_epochs):
        train_l_sum, train_acc_sum, n = 0.0, 0.0, 0
        for X, y in train_iter:
            y_hat = net(X)
            y=y.numpy()
            y=y.flatten()
            y=torch.tensor(y)
            l = loss(y_hat, y.long()).sum()  

            # 梯度清零
            if optimizer is not None:
                optimizer.zero_grad()
            elif params is not None and params[0].grad is not None:
                for param in params:
                    param.grad.data.zero_()
            
            l.backward()
            if optimizer is None:
               for param in params:
                   param.data-=lr*param.grad/batch_size
            else:
                optimizer.step()  

            train_l_sum += l.item()
            train_acc_sum += (y_hat.argmax(dim=1) == y.long()).sum().item()
            n += y.shape[0]
        test_acc = evaluate_accuracy(test_iter,net)
        print('epoch %d, loss %.4f, train acc %.3f, test acc %.3f'% (epoch + 1, train_l_sum / n, train_acc_sum / n, test_acc))

train(net,train_iter,test_iter,loss,num_epochs,batch_size,None,None,optimizer)

#预测
def get_fashion_mnist_labels(labels):
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat','sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]

X,y=iter(test_iter).next()
true_labels=get_fashion_mnist_labels(y.numpy())
pred_labels=get_fashion_mnist_labels(net(X).argmax(dim=1).numpy())
print(true_labels[0:9])
print(pred_labels[0:9])

运行结果如下：

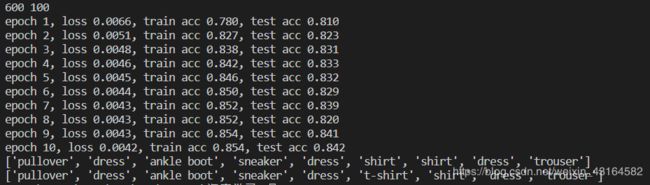
参考链接：
http://zh.d2l.ai/chapter_deep-learning-basics/linear-regression.html
https://github.com/ShusenTang/Dive-into-DL-PyTorch/blob/master/docs/chapter03_DL-basics/3.7_softmax-regression-pytorch.md