- Django学习笔记:(五)模板过滤器
码农葫芦侠
Djangodjango学习笔记
模板过滤器1简介2语法3常见过滤器3.1add3.2addslashes3.3center3.4cut3.6date3.6default3.7default_if_none3.8dictsort3.9dictsortreversed3.10lower3.11filesizeformat3.12upper3.13first3.14last3.15floatformat3.16iriencode3.1
- STM32+w5500+TcpClient学习笔记
结城明日奈是我老婆
嵌入式stm32学习笔记
文章目录参考文章本地和远程IP连接的配置(重点)TCP发送参考文章注意:SPI的CSRST脚这些都是通过cubeMX自定义的可以自行修改。用的是SPI1项目地址//MyTcpClient.h#ifndefMYTCPCLIENT_H#defineMYTCPCLIENT_H#include"main.h"#include"w5500.h"#include"socket.h"#include"wizch
- pyQT学习笔记——Qt常用组件与绘图类的使用指南
tt555555555555
Qtpyqt学习笔记
Qt常用组件与绘图类的使用指南一、大小策略(SizePolicy)1.1大小策略概述1.2具体参数1.3其他常见策略1.4伸展值的作用二、常用组件的使用2.1QSpinBox和QComboBox示例代码2.2QDialog示例代码2.3QTableView示例代码三、QPainter类介绍3.1QPainter的使用示例代码3.2QPainter的功能一、大小策略(SizePolicy)1.1大小
- PyQt5学习笔记,带例子源码
一、很程序员,都喜欢开发windows桌面应用系统,基于python3开发,效率高二、PyQt5开发的桌面应用系统是可以跨平台的,可以在Mac上、Window上、Linux桌面系统上运行,以下为学习笔记及总级三、源码下载登录后复制1、QDateTimeEdit日期输入框setCalendarPopup弹出日期选择框setDisplayFormat("yyyy-MM-ddHH:mm:ss")设置展示
- PyQt5学习笔记
Shane1111111
qt学习笔记
来源:王铭东老师的B站教程链接:PyQt5快速入门_哔哩哔哩_bilibili基本控件QRadioButtonQLineedit#清空xxx.clear()#插入新内容到最右光标处xxx.insert("内容")布局1.水平布局创建组#hobby主要是保证他们是一个组。hobby_box=QGroupBox("爱好")设置hobby_box的布局将组中内容添加到该组的容器中将组hobby_box添
- PyQT5 新手入门学习笔记
UncleShuShuShu
python的坑pythonpyqt5
一、PyQt5的起点第一个简单的pyqt程序#创建一个label程序(QLabel模块)importsysfromPyQt5.QtWidgetsimportQApplication,QLabelif__name__=='__main__':app=QApplication(sys.argv)label=QLabel('helloworld')#label的setText方法:label=Qlabe
- 《有关写书评文章的写作框架》
千江雪_2932
11月5日书评比读后感难写,对于新手来说,要先掌握好写书评的套路和写作框架,然后先按着框架写,要不写着写着就写成读后感去了。因为想要写书评,所以,正在不断学习的过程中,今天发现有这么一篇文章,作者把书评的写作框架和过程说的非常的清楚。所以学习笔记了。写文章都要谋篇布局,写书评也是一样的,先列出主题和文章框架。以下是最简单也是最常见的书评文章框架。1、开篇破题2、引出书的内容梗概及作者简介3、用一个
- 你活着可能已经死了-《得到》“武志红的心理学课”学习笔记28
大庆思考笔记
人生由几百、几千乃至几万个大大小小的选择构成,等你老了,回顾一生的时候,你发现最亏待的,恰恰是你自己,那你这一生,就白活了。我们来做一个调查,很简单,然而也许很“致命”:你能不能想起五件事,你特别想做的,但却一直没有去做的,就按照自由联想的顺序,把这五件事写出来。现在,你可以做你自己的“父母”,试试带着点偏执劲,去追逐一些你特别想追逐的事物,以此来滋养你的本我。分享一段鲁米的诗给你:有一颗光的种子
- ReactiveCocoa 学习笔记七(RACCommand)
那夜的星空分外清澈
ReactiveCocoaReactiveCocoa
RACCommandRACCommand关键的两个方法如下,理解了他们便能理解RACCommand的作用。-(instancetype)initWithEnabled:(nullableRACSignal*)enabledSignalsignalBlock:(RACSignal*(^)(InputType_Nullableinput))signalBlock;-(RACSignal*)execut
- C语言学习笔记:do..while循环、goto语句
女巫和她的乌鸦
C语言c语言学习
do…while()循环,do语句的语法:do循环语句;while(表达式);例:intmain(){inti=1;do{printf("%d",i);i++;}while(i#include#includevoidmenu(){printf("1.play\n");printf("0.exit\n");}voidgame(){//猜数字游戏的实现:先生成随机数-->猜数字。rand函数返回了一个
- Kubernetes学习笔记(四)--Pod 状态与生命周期管理
Mr小三
Kubernetes云原生kubernetes
文章目录四、Pod状态与生命周期管理1.Pod概念网络存储用法pod的终止2.Init容器init模板用途3.Pause容器4.Pod的生命周期Podphase(阶段)Pod状态5.Pod健康-容器探针(Probe)概念EXEC探针HTTP探针TCPSocket探针四、Pod状态与生命周期管理Pod是kubernetes中最重要的基本概念,在kubernetes中最小的管理元素不是一个个独立的容器
- c语言如何宏定义枚举型结构体,C语言学习笔记--枚举&结构体
搁浅的鲎
c语言如何宏定义枚举型结构体
枚举枚举是一种用户定义的数据类型,它用关键字enum以如下语法格式来声明:enum枚举类型名字{名字0,名字1,。。。,名字n};枚举类型名字通常并不真的使用,要用的是大括号里面的名字,因为它们就是常量符号,它们的类型是int,值则依次从0到n。如:enumcolor{red,yellow,green};就创建了3个常量,red的值是0,yellow的值是1,green的值是2。当需要一些可以排列
- 学习笔记(39):结合生活案例,介绍 10 种常见模型
宁儿数据安全
#机器学习学习笔记生活
学习笔记(39):结合生活案例,介绍10种常见模型线性回归只是机器学习的“冰山一角”!根据不同的任务场景(分类、回归、聚类等),还有许多强大的模型可以选择。下面我用最通俗易懂的语言,结合生活案例,介绍10种常见模型及其适用场景:一、回归模型(预测连续值,如房价)1.决策树(DecisionTree)原理:像玩“20个问题”游戏,通过一系列判断(如“面积是否>100㎡?”“房龄是否0.5就判为“会”
- Java Script学习笔记(1)
MERRYME2
笔记java学习javascript
JavaScript学习笔记(1)(课程:黑马程序员)JavaScript是什么JavaScript是世界最流行的语言之一,是一种运行在客户端的脚本语言(Script是脚本的意思)脚本语言:不需要编译,运行过程中由js解释器(js引擎)逐行来进行解释并执行现在也可以基于Node.js技术进行服务器端编程JS的组成ECMAScript(JavaScript语法)和DOM(页面文档对象)和BOM(浏览
- Java-Script学习笔记-1
许我写余生ღ
JavaScript学习javascript前端
文章目录前言JavaScript基本介绍一、js的嵌入方法内嵌式外链式行内式二、js简单语法语句注释变量JavaScript保留关键字三、JavaScript作用域Javascrpt局部变量JavaScript全局变量四、运算符算术运算符比较运算符赋值运算符逻辑运算符五、JavaScript数据类型JavaScript如何判断数据类型数字类型(Number)字符串型(string)布尔类型(boo
- 【JS笔记】Java Script学习笔记
JavaScript输出语句document.write():将内容写入html文档console.log():将内容写入控制台alert():弹窗变量JS是弱类型语言,变量无类型var:全局变量,可重复声明let:局部变量,不可重复声明const:常量,不可重复声明数据类型number:数字。整数、浮点数、NaNstring:字符串。单引号:'Hello'双引号:"Hello"模板字符串:使用反
- git 入门
格林姆大师
git入门学习笔记----3个入门命令:gitinit、gitadd、gitcommit-v学习场景(首次在github上创建newrepository):…orcreateanewrepositoryonthecommandlineecho"#blog-02">>README.mdgitinitgitaddREADME.mdgitcommit-m"firstcommit"gitremoteadd
- OpenHarmony解读之设备认证:解密流程全揭秘
陈乔布斯
HarmonyOS鸿蒙开发OpenHarmonyharmonyosopenHarmony嵌入式硬件鸿蒙开发respons
往期推文全新看点(文中附带最新·鸿蒙全栈学习笔记)①鸿蒙应用开发与鸿蒙系统开发哪个更有前景?②嵌入式开发适不适合做鸿蒙南向开发?看完这篇你就了解了~③对于大前端开发来说,转鸿蒙开发究竟是福还是祸?④鸿蒙岗位需求突增!移动端、PC端、IoT到底该怎么选?⑤记录一场鸿蒙开发岗位面试经历~⑥持续更新中……一、概述本文重点介绍客户端收到end响应消息之后的处理过程。二、源码分析这一模块的源码位于:/bas
- 前端学习笔记:React.js中state和props的区别和联系
文章目录1.`props`(属性)定义用途示例2.`state`(状态)定义用途示例3.核心区别4.常见使用场景props的场景state的场景5.交互模式父组件修改子组件状态子组件通知父组件6.最佳实践总结在React.js中,state和props是两个核心概念,用于管理组件的数据和数据流。它们的设计目的不同,但共同构成了React组件的状态管理系统。1.props(属性)定义外部传入的数据:
- C++ 11 Lambda表达式和min_element()与max_element()的使用_c++ lamda函数 min_element((1)
2401_84976182
程序员c语言c++学习
既有适合小白学习的零基础资料,也有适合3年以上经验的小伙伴深入学习提升的进阶课程,涵盖了95%以上CC++开发知识点,真正体系化!由于文件比较多,这里只是将部分目录截图出来,全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频,并且后续会持续更新如果你需要这些资料,可以戳这里获取#include#include#includeusingnamespacestd;boolcmp(int
- 算法学习笔记:17.蒙特卡洛算法 ——从原理到实战,涵盖 LeetCode 与考研 408 例题
在计算机科学和数学领域,蒙特卡洛算法(MonteCarloAlgorithm)以其独特的随机抽样思想,成为解决复杂问题的有力工具。从圆周率的计算到金融风险评估,从物理模拟到人工智能,蒙特卡洛算法都发挥着不可替代的作用。本文将深入剖析蒙特卡洛算法的思想、解题思路,结合实际应用场景与Java代码实现,并融入考研408的相关考点,穿插图片辅助理解,帮助你全面掌握这一重要算法。蒙特卡洛算法的基本概念蒙特卡
- 分布式学习笔记_04_复制模型
NzuCRAS
分布式学习笔记架构后端
常见复制模型使用复制的目的在分布式系统中,数据通常需要被分布在多台机器上,主要为了达到:拓展性:数据量因读写负载巨大,一台机器无法承载,数据分散在多台机器上仍然可以有效地进行负载均衡,达到灵活的横向拓展高容错&高可用:在分布式系统中单机故障是常态,在单机故障的情况下希望整体系统仍然能够正常工作,这时候就需要数据在多台机器上做冗余,在遇到单机故障时能够让其他机器接管统一的用户体验:如果系统客户端分布
- 算法学习笔记:15.二分查找 ——从原理到实战,涵盖 LeetCode 与考研 408 例题
呆呆企鹅仔
算法学习算法学习笔记考研二分查找
在计算机科学的查找算法中,二分查找以其高效性占据着重要地位。它利用数据的有序性,通过不断缩小查找范围,将原本需要线性时间的查找过程优化为对数时间,成为处理大规模有序数据查找问题的首选算法。二分查找的基本概念二分查找(BinarySearch),又称折半查找,是一种在有序数据集合中查找特定元素的高效算法。其核心原理是:通过不断将查找范围减半,快速定位目标元素。与线性查找逐个遍历元素不同,二分查找依赖
- OKHttp3源码分析——学习笔记
Sincerity_
源码相关Okhttp源码解析读书笔记httpclientcache
文章目录1.HttpClient与HttpUrlConnection的区别2.OKHttp源码分析使用步骤:dispatcher任务调度器,(后面有详细说明)Request请求RealCallAsyncCall3.OKHttp架构分析1.异步请求线程池,Dispather2.连接池清理线程池-ConnectionPool3.缓存整理线程池DisLruCache4.Http2异步事务线程池,http
- Python学习笔记5|条件语句和循环语句
iamecho9
Python从0到1学习笔记python学习笔记
一、条件语句条件语句用于根据不同的条件执行不同的代码块。1、if语句基本语法:if布尔型语句1:代码块#语句1为True时执行的代码示例:age=int(input("请输入你的年龄:"))ifage>=18:print("你已成年")2、if-else语句如果if条件不成立,则执行else代码块:if布尔型语句1:代码块#语句1为True时执行的代码else:代码块#语句1为False时执行的代
- 5G标准学习笔记14 - CSI--RS概述
刘孬孬沉迷学习
5G学习笔记信息与通信
5G标准学习笔记14-CSI–RS概述大家好~,这里是刘孬孬,今天带着大家一起学习一下5GNR中一个非常非常重要的参考信号------------------CSI-RS信号,CSI-RS不是持续发送,UE只能在网络明确配置了CSI-RS的情况下才能使用其进行信道测量。前言对于CSI-RS,肯定还离不开前面所说的CSI(channelstateinformation),前面也讲过CSI对于MIMO
- 5G标准学习笔记06-基于AI/ML波束管理
刘孬孬沉迷学习
5G学习笔记
5G标准学习笔记06-基于AI/ML波束管理前言前面对于孬孬学习了波束管理的概述,下面要进一步来看一下传统波束管理和现在3GPP中推动的AL/ML波束管理之前的区别联系。一、传统波束管理方法流程传统BM流程主要包括以下步骤:波束扫描(BeamSweeping):gNB通过顺序发送多个窄波束(SSB或CSI-RS),覆盖整个服务区域,UE测量每个波束的信号质量(如L1-RSRP或L1-SINR)。波
- 5G标准学习笔记03- CSI 反馈增强概述
刘孬孬沉迷学习
5G笔记学习
5G标准学习笔记03-CSI反馈增强概述大家好,最近在研究AI/ML3gpp标准NR空口的有关内容,后面可能会给大家介绍一下对应的有关内容AI/ML在3GPP标准中的研究进展在AI/ML在NR空口的应用中,对应标准主要聚焦了3个case进行讨论研究分别是:CSI反馈增强;波束管理;定位精度增强;这三个内容可能比较涉及RAN1/2的具体内容,后面会基于这个进行一定的介绍。今天主要是主要介绍CSI反馈
- 学习笔记(33):matplotlib绘制简单图表-绘制混淆矩阵热图
宁儿数据安全
#机器学习学习笔记matplotlib
学习笔记(33):matplotlib绘制简单图表-绘制混淆矩阵热图一、绘制混淆矩阵热图代码解析1.1、导入必要的库importmatplotlib.pyplotaspltfromsklearn.metricsimportconfusion_matriximportseabornassnsmatplotlib.pyplot:Python中最常用的绘图库,用于创建各种图表confusion_matr
- LLaMA 学习笔记
AI算法网奇
深度学习基础人工智能深度学习
目录LLaMA模型结构:模型微调手册:推理示例:指定位置加载模型测试ok:模型下载:llama-stack下载modelscope下载LLaMA优化技术RMSNormSwiGLU激活函数旋转位置编码(RoPE)LLaMA模型结构:llama3结构详解-CSDN博客模型微调手册:大模型微调LLaMA详细指南(准备环境、数据、配置微调参数+微调过程)_llama微调-CSDN博客显存占用:FP16/B
- scala的option和some
矮蛋蛋
编程scala
原文地址:
http://blog.sina.com.cn/s/blog_68af3f090100qkt8.html
对于学习 Scala 的 Java™ 开发人员来说,对象是一个比较自然、简单的入口点。在 本系列 前几期文章中,我介绍了 Scala 中一些面向对象的编程方法,这些方法实际上与 Java 编程的区别不是很大。我还向您展示了 Scala 如何重新应用传统的面向对象概念,找到其缺点
- NullPointerException
Cb123456
androidBaseAdapter
java.lang.NullPointerException: Attempt to invoke virtual method 'int android.view.View.getImportantForAccessibility()' on a null object reference
出现以上异常.然后就在baidu上
- PHP使用文件和目录
天子之骄
php文件和目录读取和写入php验证文件php锁定文件
PHP使用文件和目录
1.使用include()包含文件
(1):使用include()从一个被包含文档返回一个值
(2):在控制结构中使用include()
include_once()函数需要一个包含文件的路径,此外,第一次调用它的情况和include()一样,如果在脚本执行中再次对同一个文件调用,那么这个文件不会再次包含。
在php.ini文件中设置
- SQL SELECT DISTINCT 语句
何必如此
sql
SELECT DISTINCT 语句用于返回唯一不同的值。
SQL SELECT DISTINCT 语句
在表中,一个列可能会包含多个重复值,有时您也许希望仅仅列出不同(distinct)的值。
DISTINCT 关键词用于返回唯一不同的值。
SQL SELECT DISTINCT 语法
SELECT DISTINCT column_name,column_name
F
- java冒泡排序
3213213333332132
java冒泡排序
package com.algorithm;
/**
* @Description 冒泡
* @author FuJianyong
* 2015-1-22上午09:58:39
*/
public class MaoPao {
public static void main(String[] args) {
int[] mao = {17,50,26,18,9,10
- struts2.18 +json,struts2-json-plugin-2.1.8.1.jar配置及问题!
7454103
DAOspringAjaxjsonqq
struts2.18 出来有段时间了! (貌似是 稳定版)
闲时研究下下! 貌似 sruts2 搭配 json 做 ajax 很吃香!
实践了下下! 不当之处请绕过! 呵呵
网上一大堆 struts2+json 不过大多的json 插件 都是 jsonplugin.34.jar
strut
- struts2 数据标签说明
darkranger
jspbeanstrutsservletScheme
数据标签主要用于提供各种数据访问相关的功能,包括显示一个Action里的属性,以及生成国际化输出等功能
数据标签主要包括:
action :该标签用于在JSP页面中直接调用一个Action,通过指定executeResult参数,还可将该Action的处理结果包含到本页面来。
bean :该标签用于创建一个javabean实例。如果指定了id属性,则可以将创建的javabean实例放入Sta
- 链表.简单的链表节点构建
aijuans
编程技巧
/*编程环境WIN-TC*/ #include "stdio.h" #include "conio.h"
#define NODE(name, key_word, help) \ Node name[1]={{NULL, NULL, NULL, key_word, help}}
typedef struct node { &nbs
- tomcat下jndi的三种配置方式
avords
tomcat
jndi(Java Naming and Directory Interface,Java命名和目录接口)是一组在Java应用中访问命名和目录服务的API。命名服务将名称和对象联系起来,使得我们可以用名称
访问对象。目录服务是一种命名服务,在这种服务里,对象不但有名称,还有属性。
tomcat配置
- 关于敏捷的一些想法
houxinyou
敏捷
从网上看到这样一句话:“敏捷开发的最重要目标就是:满足用户多变的需求,说白了就是最大程度的让客户满意。”
感觉表达的不太清楚。
感觉容易被人误解的地方主要在“用户多变的需求”上。
第一种多变,实际上就是没有从根本上了解了用户的需求。用户的需求实际是稳定的,只是比较多,也比较混乱,用户一般只能了解自己的那一小部分,所以没有用户能清楚的表达出整体需求。而由于各种条件的,用户表达自己那一部分时也有
- 富养还是穷养,决定孩子的一生
bijian1013
教育人生
是什么决定孩子未来物质能否丰盛?为什么说寒门很难出贵子,三代才能出贵族?真的是父母必须有钱,才能大概率保证孩子未来富有吗?-----作者:@李雪爱与自由
事实并非由物质决定,而是由心灵决定。一朋友富有而且修养气质很好,兄弟姐妹也都如此。她的童年时代,物质上大家都很贫乏,但妈妈总是保持生活中的美感,时不时给孩子们带回一些美好小玩意,从来不对孩子传递生活艰辛、金钱来之不易、要懂得珍惜
- oracle 日期时间格式转化
征客丶
oracle
oracle 系统时间有 SYSDATE 与 SYSTIMESTAMP;
SYSDATE:不支持毫秒,取的是系统时间;
SYSTIMESTAMP:支持毫秒,日期,时间是给时区转换的,秒和毫秒是取的系统的。
日期转字符窜:
一、不取毫秒:
TO_CHAR(SYSDATE, 'YYYY-MM-DD HH24:MI:SS')
简要说明,
YYYY 年
MM 月
- 【Scala六】分析Spark源代码总结的Scala语法四
bit1129
scala
1. apply语法
FileShuffleBlockManager中定义的类ShuffleFileGroup,定义:
private class ShuffleFileGroup(val shuffleId: Int, val fileId: Int, val files: Array[File]) {
...
def apply(bucketId
- Erlang中有意思的bug
bookjovi
erlang
代码中常有一些很搞笑的bug,如下面的一行代码被调用两次(Erlang beam)
commit f667e4a47b07b07ed035073b94d699ff5fe0ba9b
Author: Jovi Zhang <
[email protected]>
Date: Fri Dec 2 16:19:22 2011 +0100
erts:
- 移位打印10进制数转16进制-2008-08-18
ljy325
java基础
/**
* Description 移位打印10进制的16进制形式
* Creation Date 15-08-2008 9:00
* @author 卢俊宇
* @version 1.0
*
*/
public class PrintHex {
// 备选字符
static final char di
- 读《研磨设计模式》-代码笔记-组合模式
bylijinnan
java设计模式
声明: 本文只为方便我个人查阅和理解,详细的分析以及源代码请移步 原作者的博客http://chjavach.iteye.com/
import java.util.ArrayList;
import java.util.List;
abstract class Component {
public abstract void printStruct(Str
- 利用cmd命令将.class文件打包成jar
chenyu19891124
cmdjar
cmd命令打jar是如下实现:
在运行里输入cmd,利用cmd命令进入到本地的工作盘符。(如我的是D盘下的文件有此路径 D:\workspace\prpall\WEB-INF\classes)
现在是想把D:\workspace\prpall\WEB-INF\classes路径下所有的文件打包成prpall.jar。然后继续如下操作:
cd D: 回车
cd workspace/prpal
- [原创]JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
comsci
eclipse设计模式算法工作swing
JWFD v0.96 工作流系统二次开发包 for Eclipse 简要说明
&nb
- SecureCRT右键粘贴的设置
daizj
secureCRT右键粘贴
一般都习惯鼠标右键自动粘贴的功能,对于SecureCRT6.7.5 ,这个功能也已经是默认配置了。
老版本的SecureCRT其实也有这个功能,只是不是默认设置,很多人不知道罢了。
菜单:
Options->Global Options ...->Terminal
右边有个Mouse的选项块。
Copy on Select
Paste on Right/Middle
- Linux 软链接和硬链接
dongwei_6688
linux
1.Linux链接概念Linux链接分两种,一种被称为硬链接(Hard Link),另一种被称为符号链接(Symbolic Link)。默认情况下,ln命令产生硬链接。
【硬连接】硬连接指通过索引节点来进行连接。在Linux的文件系统中,保存在磁盘分区中的文件不管是什么类型都给它分配一个编号,称为索引节点号(Inode Index)。在Linux中,多个文件名指向同一索引节点是存在的。一般这种连
- DIV底部自适应
dcj3sjt126com
JavaScript
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml&q
- Centos6.5使用yum安装mysql——快速上手必备
dcj3sjt126com
mysql
第1步、yum安装mysql
[root@stonex ~]# yum -y install mysql-server
安装结果:
Installed:
mysql-server.x86_64 0:5.1.73-3.el6_5 &nb
- 如何调试JDK源码
frank1234
jdk
相信各位小伙伴们跟我一样,想通过JDK源码来学习Java,比如collections包,java.util.concurrent包。
可惜的是sun提供的jdk并不能查看运行中的局部变量,需要重新编译一下rt.jar。
下面是编译jdk的具体步骤:
1.把C:\java\jdk1.6.0_26\sr
- Maximal Rectangle
hcx2013
max
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.
public class Solution {
public int maximalRectangle(char[][] matrix)
- Spring MVC测试框架详解——服务端测试
jinnianshilongnian
spring mvc test
随着RESTful Web Service的流行,测试对外的Service是否满足期望也变的必要的。从Spring 3.2开始Spring了Spring Web测试框架,如果版本低于3.2,请使用spring-test-mvc项目(合并到spring3.2中了)。
Spring MVC测试框架提供了对服务器端和客户端(基于RestTemplate的客户端)提供了支持。
&nbs
- Linux64位操作系统(CentOS6.6)上如何编译hadoop2.4.0
liyong0802
hadoop
一、准备编译软件
1.在官网下载jdk1.7、maven3.2.1、ant1.9.4,解压设置好环境变量就可以用。
环境变量设置如下:
(1)执行vim /etc/profile
(2)在文件尾部加入:
export JAVA_HOME=/home/spark/jdk1.7
export MAVEN_HOME=/ho
- StatusBar 字体白色
pangyulei
status
[[UIApplication sharedApplication] setStatusBarStyle:UIStatusBarStyleLightContent];
/*you'll also need to set UIViewControllerBasedStatusBarAppearance to NO in the plist file if you use this method
- 如何分析Java虚拟机死锁
sesame
javathreadoracle虚拟机jdbc
英文资料:
Thread Dump and Concurrency Locks
Thread dumps are very useful for diagnosing synchronization related problems such as deadlocks on object monitors. Ctrl-\ on Solaris/Linux or Ctrl-B
- 位运算简介及实用技巧(一):基础篇
tw_wangzhengquan
位运算
http://www.matrix67.com/blog/archives/263
去年年底写的关于位运算的日志是这个Blog里少数大受欢迎的文章之一,很多人都希望我能不断完善那篇文章。后来我看到了不少其它的资料,学习到了更多关于位运算的知识,有了重新整理位运算技巧的想法。从今天起我就开始写这一系列位运算讲解文章,与其说是原来那篇文章的follow-up,不如说是一个r
- jsearch的索引文件结构
yangshangchuan
搜索引擎jsearch全文检索信息检索word分词
jsearch是一个高性能的全文检索工具包,基于倒排索引,基于java8,类似于lucene,但更轻量级。
jsearch的索引文件结构定义如下:
1、一个词的索引由=分割的三部分组成: 第一部分是词 第二部分是这个词在多少
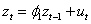 。[^1]
。[^1]