python金融大数据分析笔记----第十章 2（风险测量）

10.4 风险测量

• VaR
• CVaR

10.4.1. 风险价值（Var）
VaR（Value at Risk，风险价值或风险溢价）是度量一项投资或投资组合可能产生的下跌风险的方法，它描述的是在一定的概率水平下（即所谓的“置信水平”），在一定的时间内，持有一种正确或资产组合可能遭受的最大损失。另外，Var值为特定时间内市场因子变动引起的潜在损失提供了一种可能性的估测。特别要注意，Var方法并不说明实际损失将超过Var值多少，它只是说明实际损失超过Var值的可能性有多大。
例如，考虑一个当日价值为100万美元的股票头寸，在30天内、 置信度为99%的情况下 VaR 为5万美元。这个 VaR 数字说明，30天内损失不超过 5 万美元的概率为99% ( 100 个案例中有 99 个）。但是，它并不说明一旦损失超过 5万美元， 损失的规模会达到什么程度，即如果最大损失为10万或者50万美元时，这种特定的“高于 VaR 的损失” 概率有多大。它所说明的只是，发生 5万美元或者更大损失的概率为 1%。

1.1 知识点补充：
(1)公式: BMS ( Black - Scholes - Merton (1973)到期指数水平)
$$S_T=S_{0}exp((r-\frac{1}{2}{\delta }^2)T+\delta \sqrt{T}z)$$
变量和参数的含义如下:

• $S_T$： $T$日的指数水平
• $S_0$：初始股票指数水平
• $r$：恒定元风险短期利字.
• $\sigma$：$S$的恒定波动率(=收益的标准差)
• $T$：到期时间
• $z$：标准正态分布随机变量

(2)关于scipy.stats.scoreatpercentile(可参考：深入浅析Python科学计算库Scipy及安装步骤)

格式：scoreatpercentile (数据集、百分比) 
stats.scoreatpercentile(name_arr,percent) 

#示例：求出95%所在位置的数值
num = stats.scoreatpercentile(arr,95) 
print num

1.2 完整代码展示：

     
      import
      numpy as np

     
      import
      scipy.stats as scs

     
      import
      matplotlib.pyplot as plt
plt.rcParams['
     
      font
     .
     
      sans
     -
     
      serif
     ']='Lisu'
plt.rcParams['
     
      axes
     .unicode_minus']=
     
      False
     

S0 = 100  #初始股票指数水平
r = 0.05  #无风险利率
sigma = 0.25 #固定波动率
T = 30 / 365. #1个月
I = 10000  #模拟次数

'''
BMS(Black-Scholes-Merton(1973)到期指数水平)
$S_T = S_0exp((r - \frac{1}{2}\delta^2)T+\delta\sqrt T z)$
'''
#z = np.random.standard_normal(I) 标准正态分布下取得I个随机数
ST = S0 * np.exp((r - 0.5 * sigma ** 2) * T + sigma * np.sqrt(T) * np.random.standard_normal(I))

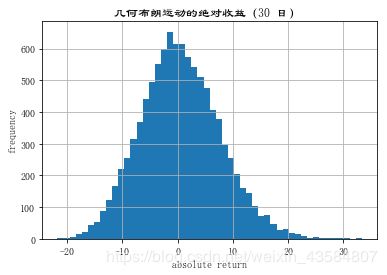
# 为了估算VaR数字，需要模拟的绝对利润和相对于近日持仓价值的亏损，并加以排序，即从最严重的亏损到最大的利润
R_gbm = np.sort(ST - S0)

#展示模拟绩效直方图
plt.hist(R_gbm, bins=50)
plt.xlabel('
     
      absolute
      
     
      return
     ')
plt.ylabel('frequency')
plt.title('几何布朗运动的绝对收益（30 日） ')
plt.grid(
     
      True
     )
plt.show()

#在列表对象percs中，将0.1转换为置信度100%-0.1%=99.9%。
percs = [0.01, 0.1, 1., 2.5, 5., 10.]
#本例中，置信度99.9%的Var为23.1货币单位，而90%置信度下为 8.7499个货币单位 。
var1 = scs.scoreatpercentile(R_gbm, percs) #计算R_gbm在percs位置的数值

     
      print
     ("%16s %16s" % ('
     
      Confidence
      
     
      Level
     ', 'Value-at-Risk(1)'))

     
      print
     (33 * '-')
for pair in zip(percs, var1):
    
     
      print
     ("%16.2f %16.4f" % (100 - pair[0], -pair[1]))

# =============================================================================
# Meron的跳跃扩散 动态模拟
# =============================================================================

lamb = 0.75
mu = -0.6
delta = 0.25
M = 50
dt = 30. / 365 / M
rj = lamb * (np.exp(mu + 0.5 * delta ** 2) - 1)
S = np.zeros((M + 1, I))
S[0] = S0

# 为了模拟跳跃扩散,需要生成3组（独立）随机数：
sn1 = np.random.standard_normal((M + 1, I))
sn2 = np.random.standard_normal((M + 1, I))
poi = np.random.poisson(lamb * dt, (M + 1, I))
for t in 
     
      range
     (1, M + 1, 1):
    S[t] = S[t - 1] * (np.exp((r - rj - 0.5 * sigma ** 2) * dt
                              + sigma * np.sqrt(dt) * sn1[t])
                       + (np.exp(mu + delta * sn2[t]) - 1)
                       * poi[t])
    S[t] = np.maximum(S[t], 0)
R_jd = np.sort(S[-1] - S0)


var2 = scs.scoreatpercentile(R_jd, percs)

     
      print
     ("%16s %16s" % ('
     
      Confidence
      
     
      Level
     ', 'Value-at-Risk(2)'))

     
      print
     (33 * '-')
for pair in zip(percs, var2):
    
     
      print
     ("%16.2f %16.3f" % (100 - pair[0], -pair[1]))

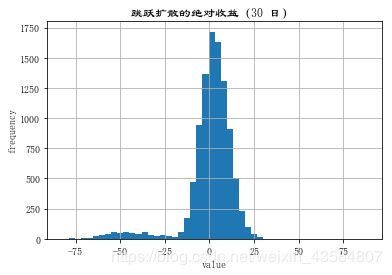
plt.hist(R_jd, bins=50)
plt.xlabel('value')
plt.ylabel('frequency')
plt.title('跳跃扩散的绝对收益（30 日） ')
plt.grid(
     
      True
     )
plt.show()

# 
     
      Confidence
      
     
      Level
      
     
      Value
     -at-
     
      Risk
     (1)
# ---------------------------------
#            99.99          23.1085
#            99.90          18.8869
#            99.00          15.0538
#            97.50          12.9250
#            95.00          11.0152
#            90.00           8.7499
# 
     
      Confidence
      
     
      Level
      
     
      Value
     -at-
     
      Risk
     (2)
# ---------------------------------
#            99.99           81.192
#            99.90           68.651
#            99.00           57.230
#            97.50           47.244
#            95.00           25.975
#            90.00            8.708

'''
从上面的输出可以看出，置信度 90%的 30日VaR 相差很少，
但是在 99.9%置信度下与几何布朗运动相比高出 3 倍多。
这说明标准 VaR 测度在捕捉金融市场经常遇到的尾部风险方面的问题
'''

#以图形方式展示几何布朗运动和跳跃扩散的风险价值
percs1 = 
     
      list
     (np.arange(0.0, 10.1, 0.1))
gbm_var = scs.scoreatpercentile(R_gbm, percs1)
jd_var = scs.scoreatpercentile(R_jd, percs1)

plt.plot(percs1, gbm_var, 'b', lw=1.5, label='GBM')
plt.plot(percs1, jd_var, 'r', lw=1.5, label='JD')
plt.legend(loc=4)
plt.xlabel('100 - 
     
      confidence
      
     
      level
      [%]')
plt.ylabel('value-at-risk')
plt.grid(
     
      True
     )
plt.xlim(0,10)
plt.ylim(ymax=0.0)
plt.show()

 Confidence Level Value-at-Risk(1)
 ---------------------------------
            99.99          23.1085
            99.90          18.8869
            99.00          15.0538
            97.50          12.9250
            95.00          11.0152
            90.00           8.7499
 Confidence Level Value-at-Risk(2)
 ---------------------------------
            99.99           81.192
            99.90           68.651
            99.00           57.230
            97.50           47.244
            95.00           25.975
            90.00            8.708

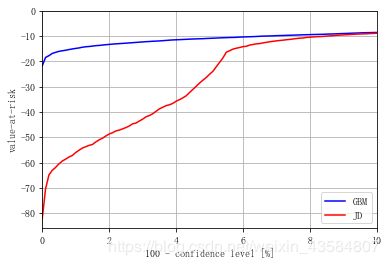
从最后一张图可以看出，在典型置信区间范围内的VaR测量表现是完全不同的。

10.4.2 信用风险价值CVaR
其他重要的风险测度是信用风险价值（CVaR）和从CVaR中派生而来的信用价值调整（CVA）。粗略地讲， CVaR 是对手方可能无法履行其义务所引发风险（例如， 对手方破产）的一个测度。在这种情况下， 有两个主要的假设：违约概率 和 （平均）损失水平。

# -*- coding: utf-8 -*-

     
      import
      numpy as np

     
      from
      numpy 
     
      import
      random

     
      import
      matplotlib.pyplot as plt
plt.rcParams['
     
      font
     .
     
      sans
     -
     
      serif
     ']='Lisu'
plt.rcParams['
     
      axes
     .unicode_minus']=
     
      False
     


     
      print
     ('*' * 30)

     
      print
     ('         考虑BSM的情况      ')

     
      print
     ('*' * 30)

# Black-Scholes-Merton 的基准设置，参数：
S0 = 100  #初始股票指数水平
r = 0.05  #无风险利率
sigma = 0.2 #固定波动率
T = 1. #1个月
I = 100000  #模拟次数
ST = S0 * np.exp((r - 0.5 * sigma ** 2) * T + 
                 sigma * np.sqrt(T) * random.standard_normal(I))

'''在最简单的请看下，人们可以考虑固定（平均）损失水平L和对手方违约（每年）概率p：'''
L = 0.5      # 固定（平均）损失水平
p = 0.01     # 对手方违约（每年）概率

# 使用泊松分布， 违约的方案可以用如下代码生成， 考虑了违约只能发生1次的事实
D = random.poisson(p * T, I)  # 泊松分布
D = np.where(D > 1, 1, D)     # 满足条件(D > 1)，输出1(，不满足输出D

# 如果没有违约，未来指数水平的风险中立价值应该等于资产当日现值（取决于数值误差造成的差异）：
without_breach_value = np.exp(-r * T) * 1 / I * np.sum(ST)

     
      print
     ('没有违约时的未来指数水平的风险中立价值 = 资产当日现值:\n',  
      
     
      round
     (without_breach_value,4))
#  99.987

# 假定条件下CVaR的计算：(假定固定（平均）损失水平L = 0.5，对手方违约（每年）概率p = 0.01)
CVaR = np.exp(-r * T) * 1 / I * np.sum(L * D * ST)

     
      print
     ('\n在有违约（L = 0.5, p = 0.01时）条件下的CVaR值:\n', 
      
     
      round
     (CVaR,4))
# 0.4971

# 经过信用风险调整之后的资产现值
S0_CVA = np.exp(-r * T) * 1 / I * np.sum((1 - L * D) * ST)

     
      print
     ('\n经过信用（条件）风险调整之后的资产现值:\n', 
     
      round
     (S0_CVA,4))
# 99.4899

# 这（S0_CVA）应该（大约）等于CVaR价值减去当前资产价值
S0_adj = S0 - CVaR

     
      print
     ('\nCVaR价值减去当前资产价值:\n', 
     
      round
     (S0_adj, 4))
# 99.5029

# 在我们假定的违约概率为1%、10万次模拟下，可以观察到由于信用风险引起的亏损大约是1000次。
credit_risk_loss = np.count_nonzero(L * D * ST)

     
      print
     ('\n由于信用风险引起的亏损的次数大约是：\n', credit_risk_loss)
# 1001

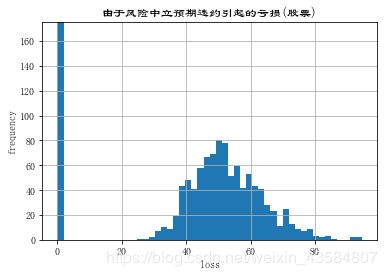
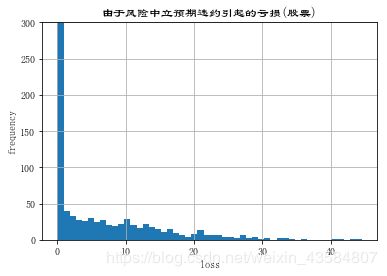
#绘图：展示由于违约引起亏损的完整频率分布，当然在大部分情况下（eg：10万例中的99000例）没有发现亏损
plt.hist(L * D * ST, bins=50)
plt.xlabel('loss')
plt.ylabel('frequency')
plt.title('由于风险中立预期违约引起的亏损（股票） ')
plt.grid(
     
      True
     )
plt.ylim(ymax=175)
plt.show()


     
      print
     ('*' * 30)

     
      print
     ('   考虑欧式看涨期权的情况      ')

     
      print
     ('*' * 30)

# 现在考虑欧式看涨期权的情况
K = 100  # 行权价100
hT = np.maximum(ST - K, 0)
C0 = np.exp(-r * T) * 1 / I * np.sum(hT)

     
      print
     ('\n行权价100时的货币价值：\n', 
     
      round
     (C0, 4))
# 10.4322
# 从输出结果可以看出，它在行权价100时的价值大约是为10.4个货币单位

CVaR1 = np.exp(-r * T) * 1 / I * np.sum(L * D * hT)

     
      print
     ('在相同的违约概率和损失水平假设下,CVaR大约是', 
     
      round
     (CVaR1, 4))
# 0.054095276121378301
# 在相同的违约概率和损失水平假设下， CVaR大约为5分

S0_CVA1 = np.exp(-r * T) * 1 / I * np.sum((1 - L * D) * hT)

     
      print
     ('调整后的期权价值大约',
     
      round
     (S0_CVA, 4))
# 10.412499028367199
# 调整后的期权价值大约低了5分


count_losses = np.count_nonzero(L * D * hT)  # 
     
      number
      of 
     
      losses
     

     
      print
     ('\n损失次数：\n', count_losses)
# 572
count_defaults = np.count_nonzero(D)  # 
     
      number
      of 
     
      defaults
     

     
      print
     ('\n违约数: \n', count_defaults)
# 1052
zero_payoff2 = I - np.count_nonzero(hT)  # 
     
      zero
      
     
      payoff
     

     
      print
     ('\n零收益数: \n', zero_payoff2)
# 44079

# 和常规资产相比， 期权有不同的特性。 
# 我们只看到略低于 500 次回违约引起的亏损。
# 但是仍然有大约1000次违约。
# 这一结果源于这样的事实：期权到期日时的收益为0的概率很大。
plt.hist(L * D * hT, bins=50)
plt.xlabel('
     
      loos
     ')
plt.ylabel('frequency')
plt.title('由于风险中立预期违约引起的亏损（看涨期权） ')
plt.grid(
     
      True
     )
plt.ylim(ymax=350)

代码改版：

# -*- coding: utf-8 -*-

     
      import
      numpy as np

     
      from
      numpy 
     
      import
      random

     
      import
      matplotlib.pyplot as plt
plt.rcParams['
     
      font
     .
     
      sans
     -
     
      serif
     ']='Lisu'
plt.rcParams['
     
      axes
     .unicode_minus']=
     
      False
     

def BMS(S0, r, sigma, T, I):
    # Black-Scholes-Merton的情况
    ST = S0 * np.exp((r - 0.5 * sigma ** 2) * T + 
                     sigma * np.sqrt(T) * random.standard_normal(I))
    
     
      return
      ST

def ECO(ST, K):
    # 考虑欧式看涨期权的情况
    hT = np.maximum(ST - K, 0)
    
     
      return
      hT

def 
     
      poisoon
     (p, I, T):
    '''在最简单的请看下，人们可以考虑固定（平均）损失水平L和对手方违约（每年）概率p：'''
    # 使用泊松分布， 违约的方案可以用如下代码生成， 考虑了违约只能发生1次的事实
    D = random.poisson(p * T, I)  # 泊松分布
    D = np.where(D > 1, 1, D)     # 满足条件(D > 1)，输出1(，不满足输出D
    
     
      return
      D

def 
     
      value
     (ST):
    r = 0.05    # 无风险利率
    T = 1.      # 1个月
    I = 100000  # 模拟次数
    # 如果没有违约，未来指数水平的风险中立价值应该等于资产当日现值（取决于数值误差造成的差异）：
    value = np.exp(-r * T) * 1 / I * np.sum(ST)   
    
     
      return
      value

#由于信用风险引起的亏损的次数
def count_loss(ST):
    credit_risk_loss = np.count_nonzero(ST)
    
     
      return
      credit_risk_loss
    
#绘图：展示由于违约引起亏损的完整频率分布，当然在大部分情况下（eg：10万例中的99000例）没有发现亏损
def 
     
      visual
     (ST, D, y=175, Str='(股票)'):
    L = 0.5     # 固定（平均）损失水平
    plt.hist(L * D * ST, bins=50)
    plt.xlabel('loss')
    plt.ylabel('frequency')
    plt.title('由于风险中立预期违约引起的亏损'+ Str)
    plt.grid(
     
      True
     )
    plt.ylim(ymax=175) if y==175 
     
      else
      plt.ylim(ymax=300)
    plt.show()

def 
     
      test
     ():
    S0 = 100    # 初始股票指数水平
    r = 0.05    # 无风险利率
    sigma = 0.2 # 固定波动率
    T = 1.      # 1个月
    I = 100000  # 模拟次数
    L = 0.5     # 固定（平均）损失水平
    p = 0.01     # 对手方违约（每年）概率
    K = 100     # 行权价100
    ST = BMS(S0, r, sigma, T, I)
    D = poisoon(p, I, T)
    
     
      print
     ('*' * 30)
    
     
      print
     ('   考虑BMS的情况      ')
    
     
      print
     ('*' * 30)
    # 如果没有违约，未来指数水平的风险中立价值应该等于资产当日现值（取决于数值误差造成的差异）：
    without_breach_value = value(ST)
    
     
      print
     ('没有违约时的未来指数水平的风险中立价值 = 资产当日现值:\n',  
          
     
      round
     (without_breach_value,4))
    # 假定条件下CVaR的计算：(假定固定（平均）损失水平L = 0.5，对手方违约（每年）概率p = 0.01)
    CVaR = value(L * D * ST)
    
     
      print
     ('\n在有违约（L = 0.5, p = 0.01时）条件下的CVaR值:\n', 
          
     
      round
     (CVaR,4))
    # 经过信用风险调整之后的资产现值
    S0_CVA = value((1 - L * D) * ST)
    
     
      print
     ('\n经过信用（条件）风险调整之后的资产现值:\n', 
     
      round
     (S0_CVA,4))
    # 这（S0_CVA）应该（大约）等于CVaR价值减去当前资产价值
    S0_adj = S0 - CVaR
    
     
      print
     ('\nCVaR价值减去当前资产价值:\n', 
     
      round
     (S0_adj, 4))
    # 在我们假定的违约概率为1%、10万次模拟下，可以观察到由于信用风险引起的亏损大约是1000次。
    credit_risk_loss1 = count_loss(L * D * ST) # 
     
      number
      of 
     
      losses
     
    count_defaults = count_loss(D)            # 
     
      number
      of 
     
      defaults
     
    zero_payoff1 = I - count_loss(ST)
    
     
      print
     ('\n由于信用风险引起的亏损的次数大约是：\n', credit_risk_loss1)
    
     
      print
     ('\n违约数: \n', count_defaults)
    
     
      print
     ('\n零收益数: \n', zero_payoff1)
    visual(ST, D)
    
    
    
     
      print
     ('*' * 30)
    
     
      print
     ('   考虑BMS的情况      ')
    
     
      print
     ('*' * 30)
    
    hT = ECO(ST, K)
    C0 = value(hT)
    
     
      print
     ('\n行权价100时的货币价值：\n', 
     
      round
     (C0, 4))
    
    CVaR1 = value(L * D * hT)
    
     
      print
     ('在相同的违约概率和损失水平假设下,CVaR大约是', 
     
      round
     (CVaR1, 4))
    # 0.054095276121378301
    # 在相同的违约概率和损失水平假设下， CVaR大约为5分

    S0_CVA = np.exp(-r * T) * 1 / I * np.sum((1 - L * D) * hT)
    
     
      print
     ('调整后的期权价值大约',
     
      round
     (S0_CVA, 4))
    # 10.412499028367199
    # 调整后的期权价值大约低了5分
    count_losses = count_loss(L * D * hT)  # 
     
      number
      of 
     
      losses
     
    # 572
    zero_payoff2 = I - count_loss(hT)  # 
     
      zero
      
     
      payoff
     
    # 44079
    
     
      print
     ('\n损失次数：\n', count_losses)
    
     
      print
     ('\n零收益: \n', zero_payoff2)
    visual(hT, D, y=350, Str='(股票)')
# 和常规资产相比， 期权有不同的特性。 
# 我们只看到略低于 500 次回违约引起的亏损。
# 但是仍然有大约1000次违约。
# 这一结果源于这样的事实：期权到期日时的收益为0的概率很大。
if __name__ == "__main__":
    test()  

输出：

******************************
考虑BMS的情况
******************************
没有违约时的未来指数水平的风险中立价值 = 资产当日现值:
99.9803

在有违约（L = 0.5, p = 0.01时）条件下的CVaR值:
0.4839

经过信用（条件）风险调整之后的资产现值:
99.4964

CVaR价值减去当前资产价值:
99.5161

由于信用风险引起的亏损的次数大约是：
960

违约数:
960

零收益数:
0

******************************
考虑BMS的情况
******************************

行权价100时的货币价值：
10.4429
在相同的违约概率和损失水平假设下,CVaR大约是 0.053
调整后的期权价值大约 10.3898

损失次数：
553

零收益:
43969

参考了python金融大数据分析的书（python2.7）也参考了Python金融大数据分析——第10章 推断统计学 笔记3
对此自我还做了些许修改，有许多不足之处，望多多指教