1、3.3编程实现对率回归
- 1、数据集
西瓜书89页数据集3.0a
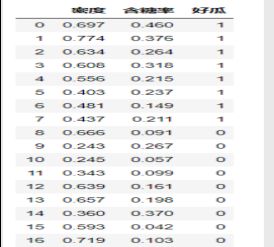
- 2、代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
dataset = pd.read_csv('watermelon3a.csv',encoding='utf-8')
X = dataset[['密度','含糖率']]
Y = dataset['好瓜']
good_melon = dataset[dataset['好瓜'] == 1]
bad_melon = dataset[dataset['好瓜'] == 0]
f1 = plt.figure(1)
plt.title('watermelon_3a')
plt.xlabel('density')
plt.ylabel('radio_sugar')
plt.xlim(0,1)
plt.ylim(0,1)
plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='*',color='r',s=50,label='bad')
plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='*',color='b',s=50,label='good')
plt.legend(loc='upper right')
X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.3,random_state=0)
log_model = LogisticRegression()
log_model.fit(X_train,Y_train)
Y_pred = log_model.predict(X_test)
print(metrics.confusion_matrix(Y_test, Y_pred))
print(metrics.classification_report(Y_test, Y_pred, target_names=['Bad','Good']))
print(log_model.coef_)
print(log_model.intercept_)
theta1, theta2 = log_model.coef_[0][0], log_model.coef_[0][1]
X_pred = np.linspace(0,1,100)
line_pred = theta1 + theta2 * X_pred
plt.plot(X_pred, line_pred)
plt.show()
- 3、输出结果
预测中正确的个数和错误的个数
准确率、查全率、F1值
系数值与最终的图形
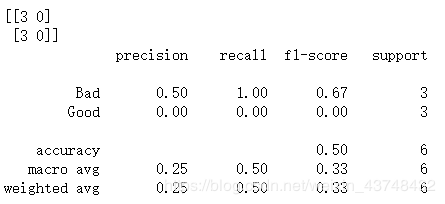
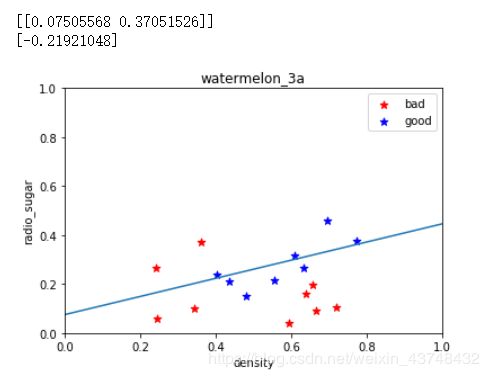
2、3.5线性判别分析
- 1、数据集
西瓜书89页数据集3.0a
- 2、理论

- 3、代码复现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn import model_selection
from sklearn import metrics
dataset = pd.read_csv('watermelon3a.csv',encoding='utf-8')
X = dataset[['密度','含糖率']]
Y = dataset['好瓜']
X_train,X_test,Y_train,Y_test = model_selection.train_test_split(X,Y,test_size=0.3,random_state=0)
LDA_model = LinearDiscriminantAnalysis()
LDA_model.fit(X_train,Y_train)
Y_pred = LDA_model.predict(X_test)
print(metrics.confusion_matrix(Y_test, Y_pred))
print(metrics.classification_report(Y_test, Y_pred, target_names=['Bad','Good']))
print(LDA_model.coef_)
good_melon = dataset[dataset['好瓜'] == 1]
bad_melon = dataset[dataset['好瓜'] == 0]
plt.scatter(good_melon['密度'],good_melon['含糖率'],marker='*',color='r',s=50,label='good')
plt.scatter(bad_melon['密度'],bad_melon['含糖率'],marker='*',color='b',s=50,label='bad')
plt.legend(loc='upper right')
plt.show()
- 输出结果
预测中正确的个数和错误的个数
准确率、查全率、F1值
系数值与最终的图形
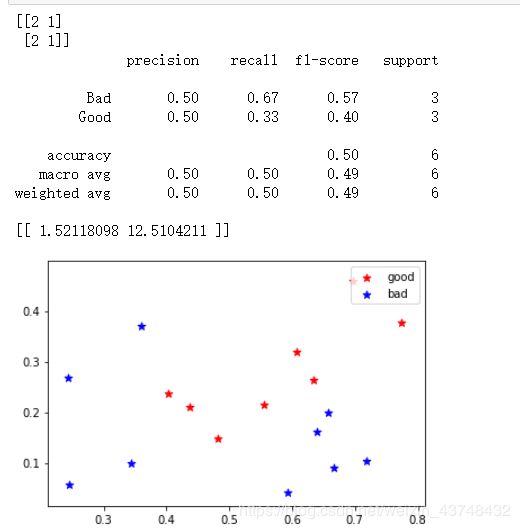
import numpy as np
import matplotlib.pyplot as plt
data = [[0.697, 0.460, 1],
[0.774, 0.376, 1],
[0.634, 0.264, 1],
[0.608, 0.318, 1],
[0.556, 0.215, 1],
[0.403, 0.237, 1],
[0.481, 0.149, 1],
[0.437, 0.211, 1],
[0.666, 0.091, 0],
[0.243, 0.267, 0],
[0.245, 0.057, 0],
[0.343, 0.099, 0],
[0.639, 0.161, 0],
[0.657, 0.198, 0],
[0.360, 0.370, 0],
[0.593, 0.042, 0],
[0.719, 0.103, 0]]
data = np.array([i[:-1] for i in data])
X0 = np.array(data[:8])
X1 = np.array(data[8:])
miu0 = np.mean(X0, axis=0).reshape((-1, 1))
miu1 = np.mean(X1, axis=0).reshape((-1, 1))
cov0 = np.cov(X0, rowvar=False)
cov1 = np.cov(X1, rowvar=False)
S_w = np.mat(cov0 + cov1)
Omiga = S_w.I * (miu0 - miu1)
plt.scatter(X0[:, 0], X0[:, 1], marker='+',color='r',s=50,label='good')
plt.scatter(X1[:, 0], X1[:, 1], marker='_',color='b',s=50,label='bad')
plt.plot([0, 1], [0, Omiga[0] / Omiga[1]], label='y')
plt.xlabel('密度', fontproperties='SimHei', fontsize=15, color='green');
plt.ylabel('含糖率', fontproperties='SimHei', fontsize=15, color='green');
plt.title(r'LinearDiscriminantAnalysis', fontproperties='SimHei', fontsize=25);
plt.legend()
plt.show()
- 结果为:


从这两种方法可以看出,线性判别方法比对率回归准确率稍高一些,效果较好,但由于数据量较少的原因,最终的效果并不是特别理想。
第五章 神经网络
3、5.5标准BP与累积BP算法
- 1、数据集
西瓜书数据集3.0

在这里参考某文章,未直接调用数据集。
- 2、理论
- 3、代码
import numpy as np
def dataSet():
X = np.mat('2,3,3,2,1,2,3,3,3,2,1,1,2,1,3,1,2;\
1,1,1,1,1,2,2,2,2,3,3,1,2,2,2,1,1;\
2,3,2,3,2,2,2,2,3,1,1,2,2,3,2,2,3;\
3,3,3,3,3,3,2,3,2,3,1,1,2,2,3,1,2;\
1,1,1,1,1,2,2,2,2,3,3,3,1,1,2,3,2;\
1,1,1,1,1,2,2,1,1,2,1,2,1,1,2,1,1;\
0.697,0.774,0.634,0.668,0.556,0.403,0.481,0.437,0.666,0.243,0.245,0.343,0.639,0.657,0.360,0.593,0.719;\
0.460,0.376,0.264,0.318,0.215,0.237,0.149,0.211,0.091,0.267,0.057,0.099,0.161,0.198,0.370,0.042,0.103\
').T
X = np.array(X)
Y = np.mat('1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0')
Y = np.array(Y).T
return X, Y
def sigmod(x):
return 1.0/(1.0+np.exp(-x))
def bpstand(hideNum):
X,Y = dataSet()
V = np.random.rand(X.shape[1],hideNum)
V_b = np.random.rand(1,hideNum)
W = np.random.rand(hideNum,Y.shape[1])
W_b = np.random.rand(1,Y.shape[1])
rate = 0.1
error = 0.001
maxTrainNum = 1000000
trainNum = 0
loss = 10
while (loss>error) and (trainNum < maxTrainNum):
for k in range(X.shape[0]):
H = sigmod(X[k,:].dot(V)-V_b)
Y_ = sigmod(H.dot(W)-W_b)
loss = sum((Y[k]-Y_)**2)*0.5
g = Y_*(1-Y_)*(Y[k]-Y_)
e = H*(1-H)*g.dot(W.T)
W += rate*H.T.dot(g)
W_b -= rate*g
V += rate*X[k].reshape(1,X[k].size).T.dot(e)
V_b -= rate*e
trainNum += 1
print("总训练次数:",trainNum)
print("最终损失:",loss)
print("V:",V)
print("V_b:",V_b)
print("W:",W)
print("W_b:",W_b)
def bpAccum(hideNum):
X,Y = dataSet()
V = np.random.rand(X.shape[1],hideNum)
V_b = np.random.rand(1,hideNum)
W = np.random.rand(hideNum,Y.shape[1])
W_b = np.random.rand(1,Y.shape[1])
rate = 0.1
error = 0.001
maxTrainNum = 1000000
trainNum = 0
loss = 10
while (loss>error) and (trainNum<maxTrainNum):
H = sigmod(X.dot(V)-V_b)
Y_ = sigmod(H.dot(W)-W_b)
loss = 0.5*sum((Y-Y_)**2)/X.shape[0]
g = Y_*(1-Y_)*(Y-Y_)
e = H*(1-H)*g.dot(W.T)
W += rate*H.T.dot(g)
W_b -= rate*g.sum(axis=0)
V += rate*X.T.dot(e)
V_b -= rate*e.sum(axis=0)
trainNum += 1
print("总训练次数:",trainNum)
print("最终损失:",loss)
print("V:",V)
print("V_b:",V_b)
print("W:",W)
print("W_b:",W_b)
if __name__ == '__main__':
bpstand(8)
bpAccum(8)
- 4、结果:
BP:
总训练次数: 69887
最终损失: [0.00099978]

累积BP:
总训练次数: 5479
最终损失: [0.0009997]
对照次数可以看出:累积BP算法比BP训练的次数要少的多
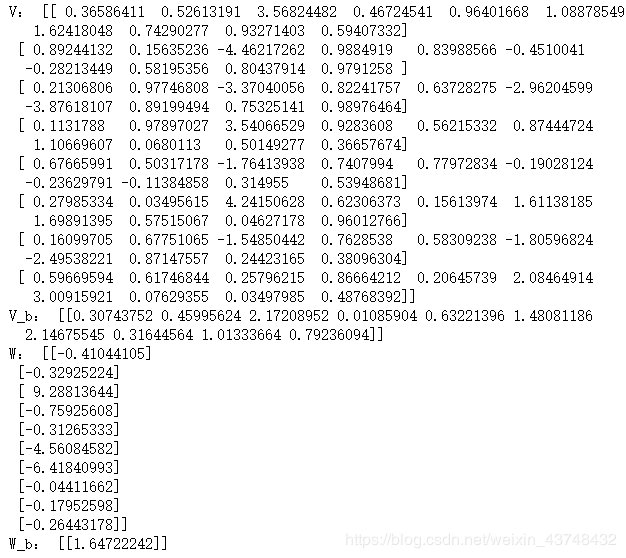
系数差别还是挺大的。









