AB测试/假设检验
文章目录
- 基础概念:
- 假设检验中的P值
- 假设检验中的α-显著性水平
- 假设检验中的1-α :置信度/置信水平
- P值与α的关系
- 双边/单边检验
- 两类错误
- 例题
- 例1:给出总体均值,和样本值,方差和样本个数
- 例2:给出两个样本总体的概率均值和样本个数
- 明确假设:
- way1: 计算H0的假设前提下的概率:P值
- way2: 计算H0的假设前提下的Z值
- 点击率等比率对比
- 例3:给出两个样本总体的均值,方差和样本个数
- F检验-方差分析 - 方差齐性检验
- 卡方检验
- 二项分布的假设检验
基础概念:
假设检验中的P值
假设检验是推断统计中的一项重要内容在假设检验中常见到P值( P-Value,Probability,Pr),P值是进行检验决策的另一个依据。
P值即概率,反映某一事件发生的可能性大小。统计学根据显著性检验方法所得到的P 值,一般以P < 0.05 为有统计学差异, P<0.01 为有显著统计学差异,P<0.001为有极其显著的统计学差异。
其含义是样本间的差异由抽样误差所致的概率小于0.05 、0.01、0.001。
H0:差别由抽样误差引起
H1: 差别不是由抽样误差引起
如果P>0.05,不能否定“差别由抽样误差引起”,则接受H0;【样本组A没有比样本组B好,】
如果P<0.05或P <0.01,可以认为差别不由抽样误差引起,可以拒绝原假设H0,则可以不拒绝另一种可能性的假设(又称备选假设,符号为H1),即两样本来自不同的总体,所以两药疗效有差别。

Attention
⑴P的意义不表示两组差别的大小,P反映两组差别有无统计学意义,并不表示差别大小。因此,与对照组相比,C药取得P<0.05,D药取得P <0.01并不表示D的药效比C强。
⑵ P>0.05时,差异无显著意义,根据统计学原理可知,不能否认无效假设,但并不认为无效假设肯定成立。在药效统计分析中,更不表示两药等效。那种将“两组差别无显著意义”与“两组基本等效”相同的做法是缺乏统计学依据的。
⑶统计学主要用上述三种P值表示,也可以计算出确切的P值,有人用P <0.001,无此必要。
⑷显著性检验只是统计结论。判断差别还要根据专业知识。抽样所得的样本,其统计量会与总体参数有所不同,这可能是由于两种原因。
假设检验中的α-显著性水平
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,用α表示。
显著性:意思是统计上的差异有多么的显著。
比如:α = 0.05,意思是有5%的可能性犯错,然而因为5%已经是一个小概率事件,因此认为当假设检验的P值<=α的时候,在两个样本总体之间的差异在统计上有显著差异,而不是因为样本抽取的随机性而引起的差异。
显著性是对差异的程度而言的,程度不同说明引起变动的原因也有不同:一类是条件差异,一类是随机差异。它是在进行假设检验时事先确定一个可允许的作为判断界限的小概率标准。
左侧检验的P值为检验统计量X 小于样本统计值C 的概率,即:P = P{ X < C}
右侧检验的P值为检验统计量X 大于样本统计值C 的概率:P = P{ X > C}
双侧检验的P值为检验统计量X 落在样本统计值C 为端点的尾部区域内的概率的2 倍:P = 2P{ X > C} (当C位于分布曲线的右端时) 或P = 2P{ X< C} (当C 位于分布曲线的左端时) 。若X 服从正态分布和t分布,其分布曲线是关于纵轴对称的,故其P 值可表示为P = P{| X| > C} 。
假设检验中的1-α :置信度/置信水平
1-α 为置信度或置信水平,其表明了区间估计的可靠性 。
P值与α的关系
P值 < α 说明小概率事件发生了,则拒绝Ho。否则接受Ho
双边/单边检验
两类错误
- 第一类错误:原假设是正确的,却拒绝了原假设。(错杀好人)
- 第二类错误:原假设是错误的,却没有拒绝原假设。(放走坏人)
- 以上发生的概率由显著性水平α的大小决定
例题
例1:给出总体均值,和样本值,方差和样本个数
某厂生产日光灯管。以往经验表明,灯管使用时间为1600h,标准差为70h,在最近生产的灯管中随机抽取了55件进行测试,测得正常使用时间为1520h。在0.05的显著性水平下,判断新生产的灯管质量是否有显著变化。

Tips:
- H0: 新灯管质量与旧灯管没有显著性差异,即新灯管的平均值u=老灯管的平均值1600
- 通过查表可知,当Z值=3.99时,在统计学上就已经可以证明 - 有100%的把握拒绝原原假设了。
例2:给出两个样本总体的概率均值和样本个数
袋子里有红豆,也有黑豆,小编想知道红豆和黑豆是不是一样多。若是一个个去看,怕是要疯了。于是我们从袋子里拿了一把豆子,看看这把红豆多还是黑豆多。用这把豆子作为样本,去推断这袋豆子。既然是用样本推断总体,就有抽样误差的可能性。不管袋子里红豆多还是黑豆多,这一把不一定能真实反映这袋豆子,那怎么办呢?
明确假设:
- 原假设 Ho:袋子里红豆和黑豆是一样多的,如果观察到红豆黑豆不一样多完全是由抽样造成的。可以转换为,现在发现的两个样本总体,红豆样本和黑豆样本是没显著差异的,两堆豆子不一样多完全是由抽样误差造成的。
- 备择假设H1:袋子里红豆和黑豆的确不一样多。
way1: 计算H0的假设前提下的概率:P值
way2: 计算H0的假设前提下的Z值

根据上述公式,p1为红豆概率0.1,n为1, p2为黑豆概率0.9,n为9,最终得到z=2.53,对应的p值为0.006.
不过上述方法有一个问题,即样本个数<30,为小样本,这个公式并不太适用于套在这里。
之后说到的t检验可能更加适合
点击率等比率对比
例3:给出两个样本总体的均值,方差和样本个数
F检验-方差分析 - 方差齐性检验
F-检定,方差分析(或译变异数分析,Analysis of Variance),是透过检视变量的方差而进行的。
它主要用于:均数差别的显著性检验、分离各有关因素并估计其对总变异 的作用、分析因素间的交互作用、方差齐性(Equality of Variances)检验等情况。
https://baike.baidu.com/item/F%E2%80%94%E6%A3%80%E9%AA%8C%E6%B3%95
https://baike.baidu.com/item/F%E6%A3%80%E9%AA%8C
https://www.cnblogs.com/nxld/p/6185433.html
卡方检验
二项分布的假设检验
小黄机智地设置了这么一个实验。他买了两大瓶可乐,一瓶可口,一瓶百事。分别分成了20杯,然后每次拿一杯可口、一杯百事放到小明面前,让小明分辨哪一杯是可口可乐。这么试验了下来,20次里面,小明答对了15次。小明说:"看,我有能力分辨吧,20次才错了5次。那5次只是不小心而已。"小黄说:“平均来说瞎猜能猜对10次,你猜对15次,只是你运气好而已,其实你根本分辨不出两种可乐。”
两人争执不下。
后来,小黄思考了一下,争执的点有两个:
(1)到底能有多大把握认为小明是瞎猜的?
(2)如果再让小明分辨一组可乐,他成功的把握有多大?
私下里学习了一下统计学知识,找到了问题的答案。
先假设小明是瞎猜的,那么小明猜对的次数X服从二项分布。可以根据二项分布的密度函数求出小明猜对0~20次的概率。
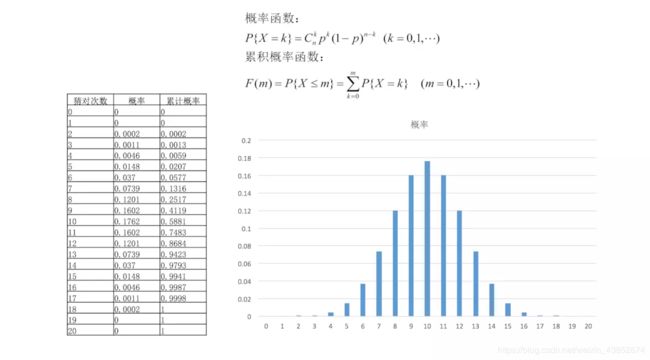
从图中的"累计概率"可以看出,如果是瞎猜的话,猜中15次及以上的概率是(1-0.9793)≈0.02。也就是说,仅凭瞎猜,猜对15次及以下的概率极小(大约2%),基本上可以认为小明不是瞎猜的。用心看一下表格就可以知道,只要小明猜对14次及以上,我们就有94%以上的把握断定小明不是瞎猜的。
虽然小明不是瞎猜的,但是他20次只对了15次,那么做单次实验,他猜对的概率是多大呢?
我们知道,伯努利分布的情况下,多次实验之后,频数对接近于概率。从已有的实验数据,我们可以猜测,小明猜对的概率是15/20=75%。
从统计学的角度来说,这是二项分布的参数p的假设检验。


