概率导论(贝叶斯统计推断)

基本问题

• 统计推断是什么？
  统计推断是从观测数据推断未知变量或未知模型的有关信息的过程。
• 统计推断的用途是什么？
  统计推断可用于“参数估计”,“假设检验”，“显著性检验”
• 统计推断的研究思路是什么?
  主要有两种思路:“贝叶斯统计推断” 和“经典统计推断”。(大局方法)
• 统计推断具体使用的"算法"有哪些？
  最大后验概率准则,最小均方估计，最大似然估计，回归，似然比检验等。(小方法)

统计学与概率论

“统计学”与“概率论”在认识论上有明显的区别。
概率论是建立在概率公理上的系统自我完善的数学课题。我们会假设一个完整的特定的概率模型满足概率公理，然后用数学方法研究模型的一些性质。概率模型无需与现实世界相一致，它值对概率公理负责。
统计学是针对一个具体的问题，寻求合理的研究方法，希望得到合理的结论。这就存在很大的自由度，采取不同的研究方法，结论可能不同。通常我们会附加一些限制条件，以便得到“理想结论”。

正是由于统计学的这种特征，现实社会存在许多人为制造的"理想结论"，这些结论可能来源于真实的数据，但研究方法是人为选定的。

贝叶斯统计与经典统计

贝叶斯统计与经典统计(频率学派)是两种突出但对立的思想学派。
最重要的区别就是如何看待未知模型或变量。贝叶斯学派将其看成已知分布的随机变量。而经典统计将其看成未知的待估计的量。
贝叶斯方法将统计拉回“概率论”的研究领域，使得每个问题只有一个答案。经典统计将未知量看作一种参数，它是一个常数，未知需要估计。
从现实角度来看，贝叶斯统计主张将假设的先验分布公开，即研究过程公开了。贝叶斯统计推断涉及到多维度积分，计算困难，所以贝叶斯学派的最新成功可能集中于如何计算上。

推断模型与推断变量

这两种问题有细微的区别。推断模型是为了研究某种现象或过程的一般规律，以期能够预测未来现象的结果。推断变量是从已知的量，推测未知的量，例如从gps信息推断所处于的位置。

术语解释

• 参数估计:对参数进行估计，使得在某种概率意义下估计接近真实值。
• 假设检验:未知参数根据对立的假设可能取有限个值，选择一个假设，目标是使犯错误的概率最小。
• 显著性检验：
• 最大后验概率(MAP)准则:给待估计的量假设一个分布，在观测条件下，最大化后验概率的值。
• 最小均方(LMS):选择数据的一个估计量或函数，使得参数与估计之间的均方误差达到最小。
• 线性最小均方(LLMS)误差:为了计算简单，简化版的LMS。

贝叶斯统计推断

流程

1. 起点是未知随机变量$\Theta$的先验分布$p_{\Theta }$或$f_{\Theta }$
2. 得到观测向量X的$p_{X|\Theta }$或$f_{X|\Theta }$
3. 一旦观测到X的一个特定值x后，运用贝叶斯法则计算$\Theta$的后验分布$p_{\Theta |X}$或$f_{\Theta |X}$

四种贝叶斯法则计算后验分布:
(省略了括号及括号内的参数，四种情形本质上是一样的，都是贝叶斯公式的运用。连续和离散的区别就是用积分号代替求和,用f代替p.分母其实都是常数，不用直接计算。)

1. $\Theta ,X$均离散。
   $$p_{\Theta |X}=\frac{p_{\Theta }{p}_{X|\Theta }}{{\sum }_{\theta }{p}_{\Theta }{p}_{X|\Theta }}$$
2. $\Theta$离散,$X$连续
   $$p_{\Theta |X}=\frac{p_{\Theta }{f}_{X}dx}{{\sum }_{\theta }{p}_{\Theta }{f}_{X|\Theta }dx}=\frac{p_{\Theta }{f}_{X|\Theta }}{{\sum }_{\theta }{p}_{\Theta }{f}_{X|\Theta }}$$
3. $\Theta$连续,$X$离散
   $$f_{\Theta |X}=\frac{f_{\Theta }\ast p_{X|\Theta }}{{\int }_{-\infty }^{+\infty }(f_{\Theta }{p}_{X|\Theta })d\theta }$$
4. $\Theta$连续,$X$连续
   $$f_{\Theta |X}=\frac{f_{\Theta }\ast f_{X|\Theta }}{{\int }_{-\infty }^{+\infty }(f_{\Theta }{f}_{X|\Theta })d\theta }$$

---

举例子:某人上班迟到时间是一个随机变量X,服从参数为$[0,\theta ]$上的均匀分布,$\theta$未知，是随机变量$\Theta$的一个值，$\Theta$服从$[0,1]$上的均匀分布。假设某次迟到时间为x。用贝叶斯推断估计$\theta$.
使用推断流程:

1. $f_{\Theta }=1,0\le \theta \le 1$
2. $f_{X|\Theta }(x|\theta )=1/\theta ,0\le x\le \theta$
3. $f_{\Theta |X}=c(x)/\theta ,x\le \theta \le 1$

---

上面这个例子得出了后验分布以后，怎样估计$\theta$值呢?引出了下一节的内容。

最大后验概率准则及应用

最大后验概率准则(Maximum a posteriori probability):知道后验概率分布以后，求此分布取最大值时的$\theta$值作为估计。其原理是在条件$X=x$下，求$\theta$最可能的值。

再次续上上面那个例子:

---

使用最大后验分布准则:要使$f_{\Theta |X}$最大化，则$\hat{\theta }=x$.
下面使用画图解释:
画出$\theta -x$的取值范围图:

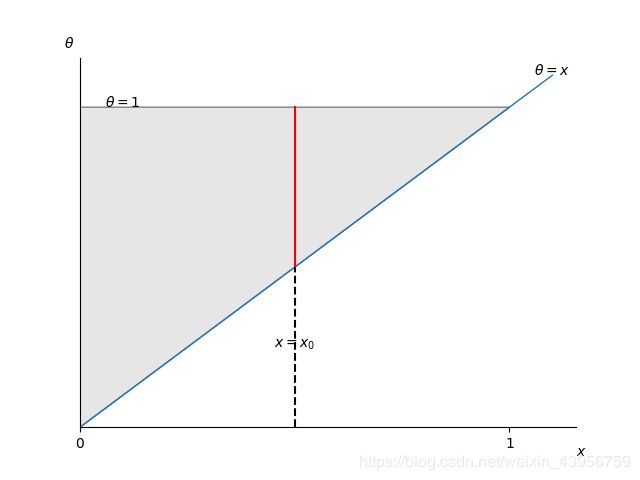
$\theta$的取值范围图中阴影部分。对于观测值$x=x_0,\theta$的取值范围为图中红线部分(但不一定是均匀分布的)。显然当$\theta =x$时能使后验概率达到最大。
可以看出,贝叶斯推断就是在确定$\theta$取值范围之后，找寻$\theta =g(x)$满足某种条件。
如果使用条件期望估计即$\theta =E(\Theta |X=x)$,注意$\Theta =g(x)$不一定是线性的。此时可以得出$\theta$的另一个估计。

---

贝叶斯最小均方估计LMS

顾名思义，最小均方估计就是求$\hat{\theta }=g(x)$使得估计误差$\hat{\theta }-\Theta$的均方误差(不是方差)达到最小。
$E[(\hat{\theta }-\Theta {)}^2]=var(\Theta )+[E(\Theta )-\hat{\theta }{]}^2$
所以最小均方误差取最小值时有:
$$\hat{\theta }=E(\Theta )$$
现在考虑在观测条件$X=x$下，最小均方误差为:
$E[(\hat{\theta }-\Theta {)}^2|X=x]=var(\Theta |X=x)+[E(\Theta |x)-\hat{\theta })]$
此时:
$$\hat{\theta }=g(x)=E(\Theta |X=x)$$
$E(\Theta |X=x)$是所有$g(x)$中能使均方误差最小的$g(x)$.

性质

最小均方误差估计及其误差：
$$\hat{\Theta }=E(\Theta |X),\tilde{\Theta }=\hat{\Theta }-\Theta$$

• $\hat{\Theta }$是无偏估计,即$E(\hat{\Theta })=E(\Theta ),E(\tilde{\Theta })=0,E(\tilde{\Theta }|X=x)=0$
• 估计误差$\tilde{\Theta }$和估计量$\hat{\Theta }$不相关:$cov(\tilde{\Theta },\hat{\Theta })=0-0=0$
• $var(\Theta )=var(\tilde{\Theta })+var(\hat{\Theta })$

多维度(多次观测及多估计参数)

在多次观测的条件下:$\hat{\Theta }=E(\Theta |X_1,X_2,...,X_n)$
这个式子难以计算，所以经常附加线性估计的约束条件，简化计算。
在多参数(${\Theta }_1,{\Theta }_2,...,{\Theta }_n$)时:
最小均方的计算式子为:$E[({\Theta }_1-{\hat{\Theta }}_1{)}^2+({\Theta }_2-{\hat{\Theta }}_2{)}^2....+({\Theta }_n-{\hat{\Theta }}_n{)}^2]$
上面的式子说明在多个待估参数时，等价于分别求单个参数的估计:${\hat{\Theta }}_i=E({\Theta }_i|X)$.

同时有多观测及多参数:
${\hat{\Theta }}_i=E({\Theta }_i|X_1,X_2,...,X_n)$.

线性最小均方估计

在计算最小均方估计时，为了计算方便，假定$\hat{\theta }$是观测值$x$的线性函数，即$g(x)$是线性函数。
多维度的情况:
$$\hat{\Theta }=a_1{X}_1+a_2{X}_2+...+a_n{X}_n+b$$
写成矩阵形式:
$$\hat{\Theta }=aX+b$$
矩阵的计算方法是:最小均方误差就是$\hat{\Theta }$到$\Theta$距离的加权和。利用加权最小二乘法可以解决这个问题。
相应的最小均方误差为:
$$E[(\Theta -\hat{\Theta }{)}^2]=E[(\Theta -a_1{X}_1-a_2{X}_2+...-a_n{X}_n-b{)}^2]$$
现在的问题就是把$a_1,a_2,...,a_n,b$当作未知数，求使整个式子取最小值时的$a_1,a_2,...,a_n,b$.

一元一次函数

先研究$n=1$时的情形，此时估计量:$\hat{\Theta }=aX+b$.
$E[(\Theta -aX-b{)}^2]=var(\Theta -aX)+[E(\Theta -aX-b){]}^2$
对于给定的a,常数b应该:$b=E(\Theta -aX)=E(\Theta )-aE(X)$
问题转化为:
$E[(\Theta -aX-E_{\Theta }+a{E}_X{)}^2]=var(\Theta -aX)$
上面是个关于a的一元二次函数,求导数的零点即可得结果：
$$a=\rho (\Theta ,X)\frac{{\sigma }_{\Theta }}{{\sigma }_X}$$
其中相关系数$\rho (\Theta ,X)=\frac{cov(\Theta ,X)}{{\sigma }_X{\sigma }_{\Theta }}.$
$$\hat{\Theta }=aX+b=\rho \frac{{\sigma }_{\Theta }}{{\sigma }_X}X+{\mu }_{\Theta }-\rho \frac{{\sigma }_{\Theta }}{{\sigma }_X}{\mu }_X$$
$$\hat{\Theta }=\rho \frac{{\sigma }_{\Theta }}{{\sigma }_X}(X-{\mu }_X)+{\mu }_{\Theta }=\frac{cov(\Theta ,X)}{{\sigma }_X^2}(X-{\mu }_X)+{\mu }_{\Theta }$$
理解:因为是估计$\Theta$，所以先给一个基准常数${\mu }_{\Theta }$.又因为已假定了$\hat{\Theta }$与$X$是线性关系，所以必然会出现相关系数$\rho$。对于X只需要取其变化信息，所以采用$(X-{\mu }_X)$去掉${\mu }_X$对于基准常数的影响。而$X$方差很大时,$(X-{\mu }_X)$也很大,方差很大的观测数据是不太好的，所以利用分母的${\sigma }_X^2$来抵消这种影响。
估计误差:
$var(\Theta -\hat{\Theta })=var(\Theta -aX-b)={\sigma }_{\Theta }^2+a^2{\sigma }_X^2-2acov(X,\Theta )=(1-{\rho }^2){\sigma }_{\Theta }^2$

多观测值和多参数

与$n=1$的情形是类似的，只不过计算更为复杂。