吴恩达深度学习 梯度下降法

笔记

逻辑回归、成本函数及梯度下降

概念以及公式

逻辑回归：对于多维空间中存在的样本点，用特征的线性组合（特征加权）去拟合空间中点的分布和轨迹，并通过在线性回归模型中引入Sigmoid函数，将线性回归的不确定范围的连续输出值映射到（0，1）范围内，成为一个概率预测问题。

成本函数：是关于参数w和b的函数，用来估量模型的预测值f(x)与真实值Y的不一致程度，衡量参数w和b在全部训练集上的效果。其函数值越小，预测结果和真实值越接近。

通过计算损失函数关于w参数的梯度来逐步调整w参数，使损失函数越来越小，达到一个极小值为止，完成模型的训练，参数达到收敛。

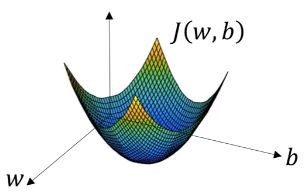
梯度下降法：对一个函数上当前点对应梯度的反方向的规定步长距离点进行迭代搜索，来找到该函数的局部极小值。如对于凸函数成本函数J，通过计算当前点的梯度来迭代更新w和b，找到一组w和b使其函数值J(w, b)最小，即全局最优解。

逻辑回归中三者联系图

梯度下降

原理

在函数中，找到给定的梯度，朝着梯度相反的方向更新变量，反复迭代，从而得到函数达到最小值时所对应的变量。

公式

• ${\theta }^1$是下一点
• ${\theta }^0$是当前给定点
• $\alpha$是学习率
• $\nabla$是向量微分算子，此处即梯度方向

梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

梯度的方向就是函数变化最快的方向

• 在单变量函数中，梯度是函数的微分，代表着函数在某个给定点的切线的斜率
• 在多变量函数中，梯度是一个向量，向量的方向支出了函数在给定点上升最快的方向。

学习率

学习率，即步长，决定了在梯度下降迭代的过程中，每一步沿梯度负方向前进的长度，控制模型的学习进度。

• 学习率选取过大，会导致易震荡、损失值爆炸。
• 学习率选取过小，会导致收敛速度慢、回归函数易过拟合。

算法过程

1. 确定当前的损失函数的梯度
2. 用步长乘以梯度，得到当前下降的距离
3. 若所有${\theta }_i$梯度下降的距离都小于$ϵ$，则算法终止，否则更新所有的${\theta }_i$，并进入步骤1

（以下部分的代码以到达迭代次数为循环结束标志）

图源来自hhhhhliu

逻辑回归中梯度下降的代数代码实现

for j in range(num_iterations):
    for i in range(m):
        z[i] = w.T * x[i] + b
        a[i] = 1 / (1 + math.exp(-z[i]))
        dz[i] = a[i] - y[i]
        for n in range(dim):
            dw[n] += x[n, i] * dz[i]
        db += dz[i]
    for n in range(dim):
        dw[n] /= m
        dw[n] = dw[n] - alpha*dw[n]
    db /= m
    b = b - a*db
    

x是维度为(n, m)的训练集_图片矩阵
y是维度为(1, m)的训练集_标签矩阵
w是维度为(n, 1)的特征矩阵
z是维度为(1, n)的回归所得矩阵
a是维度为(1, n)的预测数据
dz是维度为(1, n)的z的偏导矩阵
dw是维度为(1, n)的w的倒置的偏导矩阵
num_iterations是迭代次数
m是样本数量
dim是特征数量
alpha是学习率

逻辑回归中梯度下降的向量化代码实现

w = np.zeros((dim, 1))
b = 0
for i in range(num_iterations):
    z = np.dot(w.T, x) + b
    A = 1 / (1 + np.exp(-z))
    dz = A - Y
    dw = np.dot(x, dz.T) / m
    db = np.sum(dz) / m
    w = w - alpha*dw
    b = b - alpha*db

x是维度为(n, m)的训练集_图片矩阵
Y是维度为(1, m)的训练集_标签矩阵
w是维度为(n, 1)的特征矩阵
z是维度为(1, n)的回归所得矩阵
A是维度为(1, n)的预测数据矩阵
dz是维度为(1, n)的z的偏导矩阵
dw是维度为(1, n)的w的倒置的偏导矩阵
num_iterations是迭代次数
dim是特征数量
alpha是学习率

np.dot(w.T, x)是w的转置、x两个矩阵相乘，代替显示循环。
np.sum(z)是将z中各个元素加起来。
A-Y得到的是矩阵A和矩阵Y相减后的矩阵。

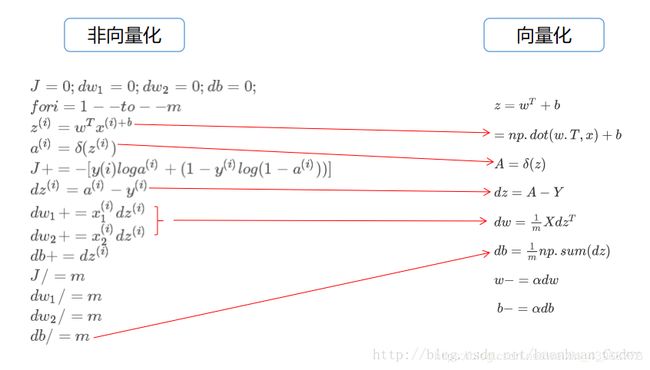
向量化和非向量化比较

向量化的程序运行速度要比非向量化的程序化的运行速度会快很多

可扩展深度学习是在GPU上做的，但是GPU和CPU都含有并行化指令有时也叫SIMD（single instruction multiple data）指令。GPU更加擅长SIMD计算。实际编程的法则是只要有可能就不能显式的使用for循环。

参考资料

深入浅出–梯度下降法及其实现
作者：六尺帐篷
来源：简书

梯度下降（Gradient Descent）小结
作者：刘建平Pinard
来源：博客园

向量化
作者：程序之巅
来源：CSDN

吴恩达深度学习–向量化
作者：hhhhhliu
来源：CSDN