一篇文章总结python机器学习类不平衡问题的处理-class imbalance（ROC，混淆矩阵，f1 score等）

source: python machine learning 3rd

所谓的类不平衡问题，指的就是数据集中一类的样本量明显小于另一类。在这类特殊问题中，如果不进行处理，默认训练模型时对小类和大类数据的惩罚相同，会导致对数据更加敏感，样本量更少的小类产生预测上的偏差。如何处理这一偏差，让模型对大类和小类都有良好的预测结果? 本文将给出总结性的方法集合

本文中python实现的数据集建议来自Breast Cancer Wisconsin dataset

混淆矩阵

---

混淆其实不是专门用来处理类不平衡问题的，但是它能够帮助我们清晰直观地分析类不平衡问题，之后我们要介绍到的种种方法，基本都要涉及到混淆矩阵的使用。

混淆矩阵能够详细地给我们展示以下四种预测情况的分布：

• TP: true positive - 样本预测结果为1，实际分类结果也为1
• TN: true negative - 样本预测结果为0，实际分类结果也为0
• FP: false positive - 样本预测结果为1， 实际分类结果为0
• FN: false negative - 样本预测结果为0，实际分类结果为1

注：本文中的y=1样本都默认表示为想要预测的种类，一般情况下都为小类

python实现

之后的所有代码都会假设X_train, y_train已获得且被合理分割

...
# 导入迷惑矩阵
from sklearn.metrics import confusion_matrix

# 使用一个模型训练数据，如此中SVC pipeline
pipe_svc.fit(X_train, y_train)
# 获得模型的预测结果
y_pred = pipe_svc.predict(X_test)
# 使用预测结果和真实结果一步生成混淆矩阵
confmat = confusion_matrix(y_true=y_test, y_pred=y_pred)

可视化:

# matplotlib
fig, ax = plt.subplots(figsize=(2.5, 2.5))
ax.matshow(confmat, cmap=plt.cm.Blues, alpha=0.3)
for i in range(confmat.shape[0]):
    for j in range(confmat.shape[1]):
        ax.text(x=j, y=i, s=confmat[i, j], va='center', ha='center')

plt.xlabel('Predicted label')
plt.ylabel('True label')

plt.tight_layout()
plt.show()

稍加注意这里的坐标分布和我们之前介绍的是反的，即0在左上角

准确度，召回率和f1 score

---

准确率(ACC/PRE)

准确率（accuracy/precision）直接反应了我们机器学习模型的表现，得分越高，预测结果的正确率越高

具体而言：
$$ERR=\frac{FP+FN}{FP+FN+TP+TN}$$
$$ACC=\frac{TP+TN}{FP+FN+TP+TN}=1-ERR$$
所以说，准确率越高，模型中预测正确的结果占比越大，一般我们使都使用准确率来表示测试集得分

召回率(REC)

尽管准确率十分常用，但是在面对类不平衡问题时，它也有很大的局限性

假设我们使用准确率为99.5%的超级棒棒模型去预测1005位体检者是否可能患有癌症，结果显示预测到的1000名患者后得到的结果全是0，也就是都没有得癌症，那么也就是说，我们漏过了5位癌症患者，无法给它们给予治疗，这个数目不多，但是假设这1005位体检者中总共只有10人患有癌症，也就其中一半的癌症患者可能因此失去尽早治疗的机会。。。。。。

癌症检测是一个很典型的类不平衡问题，分类结果为1（患癌）的患者明显少于分类结果为0的患者，此时准确率的表现令人捉急，这时就该召唤召回率上场了！
$$REC=\frac{TP}{P}=\frac{TP}{FN+TP}$$
注意REC其实就是TPR(true positive rate)，表示预测出来的正样本与真实的正样本之间的比例，按照这个公式计算我们的癌症预测模型，我们得到的结果因该是: 5/（5+5）= 50%，这个分数很明显不能让人满意

F1 score

通过之前的分析我们可以很明显地发现，准确率和召回率各有各自的侧重点，从而导致对同一问题产生的评估结果完全不同，于是乎，是否存在一种评分方法，能够完整地考虑到准确率和召回率，从而全面地评估各种机器学习模型（包括类不平衡问题）呢？答案就是F1 score

F1 score的公式非常简单:
$$F1=2\frac{PRE\times REC}{PRE+REC}$$
将我们分别计算的准确率和召回率带入即可，一般而言，尤其是在类不平衡问题中，我们认为F1 score越高，模型表现越好，这同样适用于任何情况

python 实现

# 导入三种评分方式
from sklearn.metrics import precision_score, recall_score, f1_score

print('Precision: %.3f' % precision_score(y_true=y_test, y_pred=y_pred))
print('Recall: %.3f' % recall_score(y_true=y_test, y_pred=y_pred))
# 输入真实结果和预测结果，一步搞定
print('F1: %.3f' % f1_score(y_true=y_test, y_pred=y_pred))

Precision: 0.976
Recall: 0.952
F1: 0.964

另外如果你希望定义0为positive tag时：

from sklearn.metrics import make_scorer

scorer = make_scorer(f1_score, pos_label=0)

这个得到的scorer和f1_score用法相同

ROC

---

从类不平衡问题到类相对平衡的问题，中间其实是不同种类数据的比例变化，在这个比例变化中，分析准确率和召回率的公式不难发现，这两者的评估效力也在不断变化，乃至此消彼长。此时F1 score 仍可作为比准确率更好地评价方式，但是这不意味着样本比例对模型参数的影响被消除了。

此时，ROC（Receiver Operating Characteristics 受试者特征曲线）AUC可以为我们解决这个烦恼。

ROC生成原理及性质

在此之前我们首先需要了解ROC评价的横纵坐标 - FPR 和 TPR 是怎么来的：
$$\begin{array}{rl}& FPR=\frac{FP}{N}=\frac{FP}{FP+TN}\\ & TPR=\frac{TP}{P}=\frac{TP}{FN+TP}\end{array}$$
有了这两个指标，我们可以进行阈值设定，进行阈值设定的前提是进行监督学习时不直接得到分类结果，而是采用反应样本归属的概率，最典型的就是逻辑回归，还记得逻辑回归假设方程得到的结果能够直接表示样本属于这一类的概率吗？利用这些概率，我们可以：

1. 从0开始选择阈值概率，设定低于这一概率的为0，高于这一概率的为1
2. 得到这个阈值概率下样本集的混淆矩阵
3. 通过混淆矩阵计算FPR和TPR
4. 递增选择另一概率，重复1-3步，直到概率为1
5. 绘图得到ROC曲线，ROC曲线与横坐标轴（TPR）的积分面积即为AUC（Area Under the Curve）
   
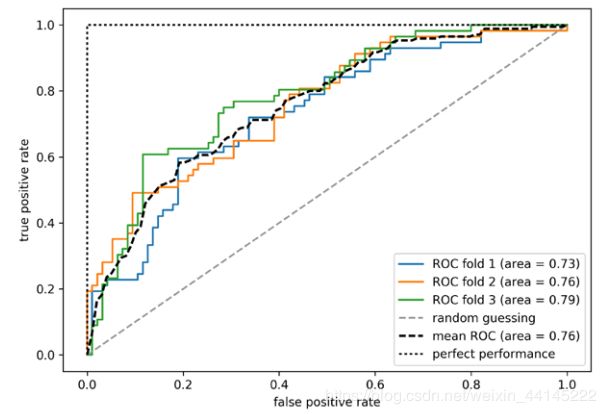
   在这个曲线中，我们又可以发现：

• ROC曲线位于随机预测曲线和完美预测曲线之间（不然又卵用）
• ROC曲线越靠近左上角，即越接近完美预测曲线越好
• 使用交叉验证的方式得到多条ROC曲线（3），然后计算平均表现，这比只计算一次要好得多
• 使用python可以顺便得到AUC，AUC越大，表现效果越好
• 选择的阈值概率增量越小，曲线越平滑

这样子得到的ROC AUC图，基本可以在数据从类不平衡问题到类平衡问题之间保持稳定，而不像F1 score那样随着数据比例可能会发生剧烈变化

python实现

python实现ROC是一个相对繁琐的过程，以下代码全部来自python machine learning 3rd，这将实现上图表现出来的ROC曲线效果

from sklearn.metrics import roc_curve, auc
from distutils.version import LooseVersion as Version
from scipy import __version__ as scipy_version


if scipy_version >= Version('1.4.1'):
    from numpy import interp
else:
    from scipy import interp


pipe_lr = make_pipeline(StandardScaler(),
                        PCA(n_components=2),
                        LogisticRegression(penalty='l2', 
                                           random_state=1,
                                           solver='lbfgs',
                                           C=100.0))

X_train2 = X_train[:, [4, 14]]
    

cv = list(StratifiedKFold(n_splits=3).split(X_train, y_train))

fig = plt.figure(figsize=(7, 5))

mean_tpr = 0.0
mean_fpr = np.linspace(0, 1, 100)
all_tpr = []

for i, (train, test) in enumerate(cv):
    probas = pipe_lr.fit(X_train2[train],
                         y_train[train]).predict_proba(X_train2[test])

    fpr, tpr, thresholds = roc_curve(y_train[test],
                                     probas[:, 1],
                                     pos_label=1)
    mean_tpr += interp(mean_fpr, fpr, tpr)
    mean_tpr[0] = 0.0
    roc_auc = auc(fpr, tpr)
    plt.plot(fpr,
             tpr,
             label='ROC fold %d (area = %0.2f)'
                   % (i+1, roc_auc))

plt.plot([0, 1],
         [0, 1],
         linestyle='--',
         color=(0.6, 0.6, 0.6),
         label='Random guessing')

mean_tpr /= len(cv)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
plt.plot(mean_fpr, mean_tpr, 'k--',
         label='Mean ROC (area = %0.2f)' % mean_auc, lw=2)
plt.plot([0, 0, 1],
         [0, 1, 1],
         linestyle=':',
         color='black',
         label='Perfect performance')

plt.xlim([-0.05, 1.05])
plt.ylim([-0.05, 1.05])
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.legend(loc="lower right")

plt.tight_layout()
plt.show()

多类分类问题-加权均分

多类问题的评分

之前我们涉及到的问题都是二元判断问题，而当我们面对多类分类问题（one vs all）的时候，如何评价一个模型在k类分类问题中的表现?

• 使用微观平均准确度(micro-average of the precision score)$$PR{E}_{\text{micro}}=\frac{T{P}_1+\cdots +T{P}_k}{T{P}_1+\cdots +T{P}_k+F{P}_1+\cdots +F{P}_k}$$每个样本一视同仁
• 使用宏观平均准确度(macro-average of the precision score)$$PR{E}_{\text{macro}}=\frac{PR{E}_1+\cdots +PR{E}_k}{k}$$每个分类一视同仁

多类类不平衡问题的评价

拥有一视同仁的方法不代表就拥有了好的评价体系，但是在多类分类问题中，一般而言，我们不再使用F1 score等方式来繁琐地计算每一种分类，而是引入加权，然后继续使用准确度作为评价依据。这样的方式已经足够帮助我们处理多类中类不平衡问题带来的影响

具体而言，对于宏观均分而言，引入的加权不是总体样本比例的加权，而是每一类的阳性样本（y=1）所占总样本阳性样本的比例，因此一个类越不平衡，它的加权越小，对总体评价的影响越小（因为此时准确率在类不平衡问题中的依据性差）
$$PR{E}_{\text{weighted-macro}}=\frac{w_{1}PR{E}_1+\cdots +w_{k}PR{E}_k}{1}$$
一般来说，宏观加权均分时scikit learn中评价多类分类问题的默认方法，一般情况下也足够处理类不平衡问题，如果由于特殊需要想使用微观均分方法的：

from sklearn.metrics import make_scorer

pre_scorer = make_scorer(score_func=precision_score, 
                         pos_label=1, 
                         greater_is_better=True, 
                         # 改为微观算法
                         average='micro')

当然，如果你觉得加权均分还无法达到你的要求，你可以去scikit learn查找更多的多类问题评价方式

其它方法

除了这些大理论，你可以通过使用一些小巧的方式来处理类不平衡问题，事实上，这些方法简单小巧，使用起来更加简单：

• 使用召回率（recall）来评价严重的类不平衡问题而不是准确率和F1 score
• 更改样本加权，加重对小类错误预测的惩罚，在scikit learn设置模型的超参数时，你可以设置class_weight='balanced'来达到这个效果
• 小类过采样，即在少数类中重复采样；大类欠采样，即在多数类中部分采样。
• 使用人工数据实现数据增强，怎么人造数据，你可参考人造数据

总之，类不平衡问题的处理同机器学习许多其它方面一样，没有恒定的真理和对应完美的解决方案。想要一个美妙的模型？你得从工具箱中一个个拿出尝试

欢迎各位的建议和补充！