深度学习基础之-4.1非线性回归-激活函数
非线性回归
当神经网络不是一层的时候,就需要对每一层的输出加一个激活函数,将输出进行非线性的映射,否则不论网络有多少层,线性的变换永远可以视为一次线性的变换,不能解决复杂问题
激活函数
看神经网络中的一个神经元,为了简化,假设该神经元接受三个输入,分别为 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3,那么 z = ∑ i w i x i + b i z=\sum\limits_{i}w_ix_i+b_i z=i∑wixi+bi,
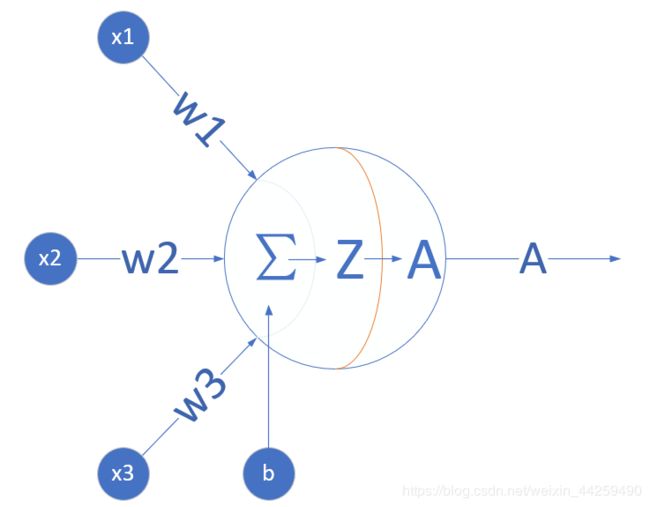
激活函数也就是 A = a ( Z ) A=a(Z) A=a(Z)这一步了,他有什么作用呢?主要是给神经网络增加非线性因素
激活函数的基本性质:
- 非线性:线性的激活函数和没有激活函数一样。
- 可导性:做误差反向传播和梯度下降,必须要保证激活函数的可导性。
- 单调性:单一的输入会得到单一的输出,较大值的输入得到较大值的输出
在物理试验中使用的继电器,是最初的激活函数的原型:当输入电流大于一个阈值时,会产生足够的磁场,从而打开下一级电源通道,如下图所示:

用到神经网络中的概念,用‘1’来代表一个神经元被激活,‘0’代表一个神经元未被激活。
这个函数有什么不好的地方呢?主要的一点就是,他的梯度(导数)恒为零(个别点除外)。反向传播公式中,梯度传递用到了链式法则,如果在这样一个连乘的式子其中有一项是零,这样的梯度就会恒为零,是没有办法进行反向传播的。
挤压型激活函数 Squashing Function(饱和型激活函数)【最多的是Sigmoid函数】
对数几率函数 Logistic Function
逻辑激活函数,逻辑分类函数,对率函数。常常被称为Sigmoid函数,因为它是最常用的Sigmoid函数。
公式:
a ( z ) = 1 1 + e − z a(z) = \frac{1}{1 + e^{-z}} a(z)=1+e−z1
导数:
a ′ ( z ) = a ( z ) ∗ ( 1 − a ( z ) ) a^{'}(z) = a(z) * (1 - a(z)) a′(z)=a(z)∗(1−a(z))
输入值域: [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
输出值域: [ 0 , 1 ] [0,1] [0,1]
函数图像:
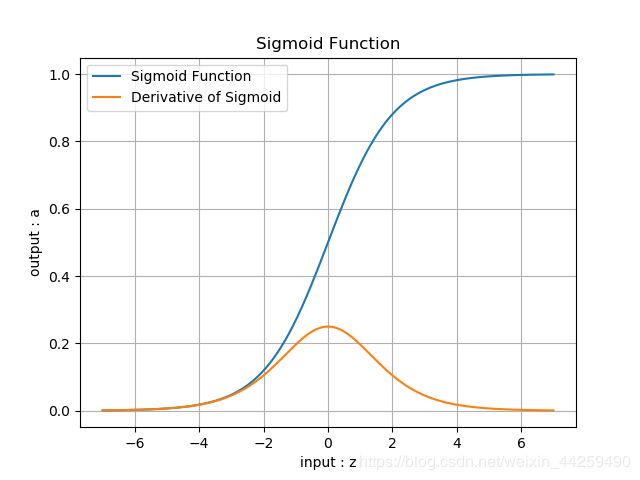
优点:
- 从函数图像来看,sigmoid函数的作用是将输入压缩到(0, 1)这个区间范围内,这种输出在0~1之间的函数可以用来模拟一些概率分布的情况。他还是一个连续函数,导数简单易求。
- 从数学上来看,Sigmoid函数对中央区的信号增益较大,对两侧区的信号增益小,在信号的特征空间映射上,有很好的效果。
- 从神经科学上来看,中央区酷似神经元的兴奋态,两侧区酷似神经元的抑制态,因而在神经网络学习方面,可以将重点特征推向中央区, 将非重点特征推向两侧区。
- 分类功能:我们经常听到这样的对白“你觉得这件事情成功概率有多大?”“我有六成把握能成功”。sigmoid函数在这里就起到了如何把一个数值转化成一个通俗意义上的把握的表示。值越大,那么这个神经元对于这张图里有这样一条线段的把握就越大,经过sigmoid函数之后的结果就越接近100%,也就是1这样一个值,表现在图里,也就是这个神经元越兴奋(亮)。
缺点:
- exp()计算代价大。
- 反向传播时梯度消失:从梯度图像中可以看到,sigmoid的梯度在两端都会接近于0,根据链式法则,如果传回的误差是 δ \delta δ,那么梯度传递函数是 δ ⋅ a ′ ( z ) \delta \cdot a'(z) δ⋅a′(z),而 a ′ ( z ) a'(z) a′(z)这时是零,也就是说整体的梯度是零。这也就很容易出现梯度消失的问题,并且这个问题可能导致网络收敛速度比较慢,比如采取MSE作为损失函数算法时。
纯粹数学的例子
假定我们的学习速率是0.2,sigmoid函数值是0.9,如果我们想把这个函数的值降到0.5,需要经过多少步呢?
我们先来做公式推导, 第一步,求出当前输入的值
1 1 + e − z = 0.9 \frac{1}{1 + e^{-z}} = 0.9 1+e−z1=0.9 e − z = 1 9 e^{-z} = \frac{1}{9} e−z=91 x = l n 9 x = ln{9} x=ln9
第二步,求出当前梯度
Δ = a ( z ) × ( 1 − a ( z ) ) = 0.9 × 0.1 = 0.09 \Delta = a(z)\times(1 - a(z)) = 0.9 \times 0.1= 0.09 Δ=a(z)×(1−a(z))=0.9×0.1=0.09
第三步,根据梯度更新当前输入值
z n e w = z − η × Δ = l n 9 − 0.2 × 0.09 = l n ( 9 ) − 0.018 z_{new} = z - \eta \times \Delta = ln{9} - 0.2 \times 0.09 = ln(9) - 0.018 znew=z−η×Δ=ln9−0.2×0.09=ln(9)−0.018
第四步,判断当前函数值是否接近0.5
1 1 + e − z n e w = 0.898368 \frac{1}{1 + e^{-z_{new}}} = 0.898368 1+e−znew1=0.898368
第五步,重复步骤2-3直到当前函数值接近0.5
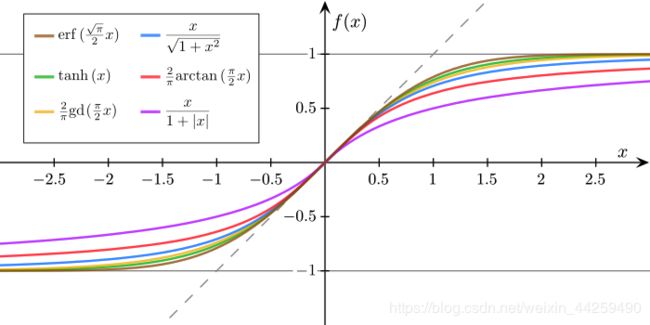
上半部分那条五彩斑斓的曲线就是迭代更新的过程了,一共迭代了多少次呢?根据程序统计,sigmoid迭代了67次才从0.9衰减到了接近0.5的水准。有同学可能会说了,才67次嘛,这个次数也不是很多啊!确实,从1层来看,这个速度还是可以接受的,但是神经网络只有这一层吗?多层叠加之后的sigmoid函数,因为反向传播的链式法则,两层的梯度相乘,每次更新的步长更小,需要的次数更多,也就是速度更加慢。如果还是没有反应过来的同学呢,可以先向下看relu函数的收敛速度。
此外,如果输入数据是(-1, 1)范围内的均匀分布的数据会导致什么样的结果呢?经过sigmoid函数处理之后这些数据的均值就从0变到了0.5,导致了均值的漂移,在很多应用中,这个性质是不好的。
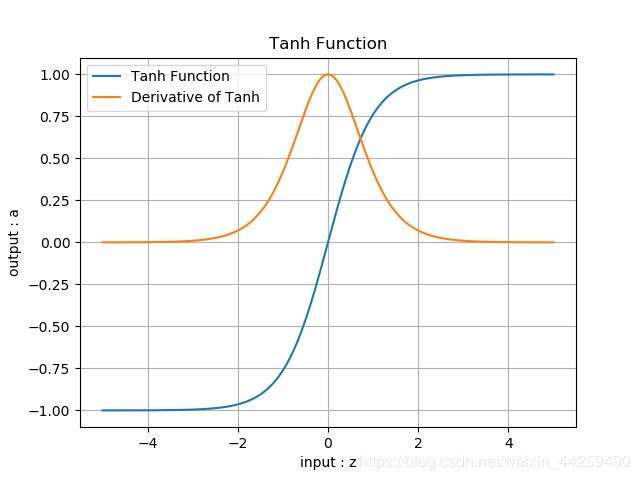
Tanh函数(TanHyperbolic,双曲正切函数)
公式:
a ( z ) = e z − e − z e z + e − z = 2 1 + e − 2 z − 1 a(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} = \frac{2}{1 + e^{-2z}} - 1 a(z)=ez+e−zez−e−z=1+e−2z2−1
a ( z ) = 2 ⋅ S i g m o i d ( 2 z ) − 1 a(z) = 2 \cdot Sigmoid(2z) - 1 a(z)=2⋅Sigmoid(2z)−1
导数公式:
a ′ ( z ) = ( 1 + a ( z ) ) ∗ ( 1 − a ( z ) ) a'(z) = (1 + a(z)) * (1 - a(z)) a′(z)=(1+a(z))∗(1−a(z))
优点:
- 具有Sigmoid的所有优点。
- 无论从理论公式还是函数图像,这个函数都是一个和sigmoid非常相像的激活函数,他们的性质也确实如此。但是比起sigmoid,tanh减少了一个缺点,就是他本身是零均值的,也就是说,在传递过程中,输入数据的均值并不会发生改变,这就使他在很多应用中能表现出比sigmoid优异一些的效果。
- 当输入数值很大或者很小时,它的导数为1,可以保证梯度不消失。
缺点:
- exp()计算代价大。
- 梯度消失。
其它函数
半线性激活函数(非饱和型激活函数)
ReLU函数(Rectified Linear Unit,修正线性单元,线性整流函数,斜坡函数。)
公式:
a ( z ) = m a x ( 0 , z ) = { z ( z ≥ 0 ) 0 ( z < 0 ) } a(z) = max(0,z) = \begin{Bmatrix} z & (z \geq 0) \ 0 & (z < 0) \end{Bmatrix} a(z)=max(0,z)={z(z≥0) 0(z<0)}
导数:
a ′ ( z ) = { 1 z ≥ 0 0 z < 0 a'(z) = \begin{cases} 1 & z \geq 0 \ 0 & z < 0 \end{cases} a′(z)={1z≥0 0z<0
输入值域: [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
输出值域: [ 0 , ∞ ] [0,\infty] [0,∞]
导数值域: [ 0 , 1 ] [0,1] [0,1]
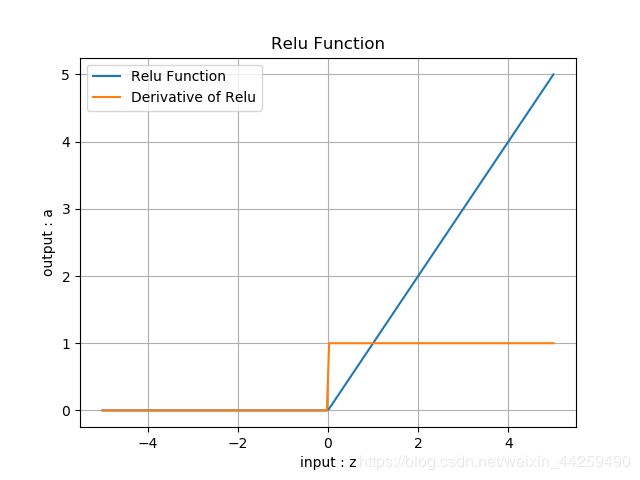
仿生学原理:
相关大脑方面的研究表明生物神经元的信息编码通常是比较分散及稀疏的。通常情况下,大脑中在同一时间大概只有1%-4%的神经元处于活跃状态。使用线性修正以及正则化(regularization)可以对机器神经网络中神经元的活跃度(即输出为正值)进行调试;相比之下,逻辑函数在输入为0时达到 ,即已经是半饱和的稳定状态,不够符合实际生物学对模拟神经网络的期望。不过需要指出的是,一般情况下,在一个使用修正线性单元(即线性整流)的神经网络中大概有50%的神经元处于激活态。
优点:
- 反向导数恒等于1,更加有效率的反向传播梯度值,收敛速度快
- 避免梯度消失问题
- 计算简单,速度快
- 活跃度的分散性使得神经网络的整体计算成本下降
缺点:
- 无界。
- 梯度很大的时候可能导致的神经元“死”掉。
而这个死掉的原因是什么呢?是因为很大的梯度导致更新之后的网络传递过来的输入是小于零的,从而导致relu的输出是0,计算所得的梯度是零,然后对应的神经元不更新,从而使relu输出恒为零,对应的神经元恒定不更新,等于这个relu失去了作为一个激活函数的梦想。问题的关键点就在于输入小于零时,relu回传的梯度是零,从而导致了后面的不更新。在学习率设置不恰当的情况下,很有可能网络中大部分神经元“死”掉,也就是说不起作用了。
用和sigmoid函数那里更新相似的算法步骤和参数,来模拟一下relu的梯度下降次数,也就是学习率 α = 0.2 \alpha = 0.2 α=0.2,希望函数值从0.9衰减到0.5,这样需要多少步呢?
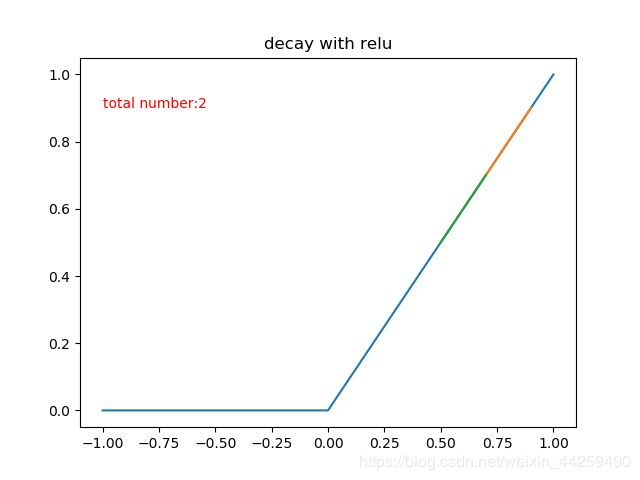
也就是说,同样的学习速率,relu函数只需要两步就可以做到sigmoid需要67步才能衰减到的程度!
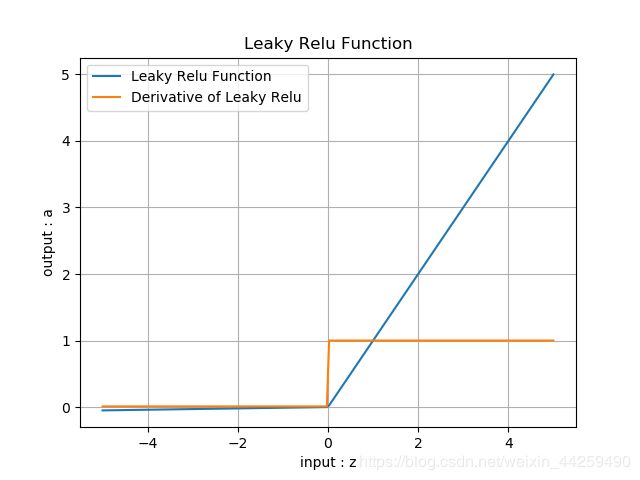
Leaky ReLU函数(带泄露的线性整流函数)
公式:
a ( z ) = { z z ≥ 0 α ∗ z z < 0 a(z) = \begin{cases} z & z \geq 0 \ \alpha * z & z < 0 \end{cases} a(z)={zz≥0 α∗zz<0
导数:
a ′ ( z ) = { z z ≥ 0 α z < 0 a'(z) = \begin{cases} z & z \geq 0 \ \alpha & z < 0 \end{cases} a′(z)={zz≥0 αz<0
输入值域: [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
输出值域: [ − ∞ , ∞ ] [-\infty,\infty] [−∞,∞]
导数值域: [ 0 , 1 ] [0,1] [0,1]
- 继承了ReLU函数的优点。
- 相比较于relu函数,leaky relu同样有收敛快速和运算复杂度低的优点,而且由于给了 x < 0 x<0 x<0时一个比较小的梯度 α \alpha α,使得 x < 0 x<0 x<0时依旧可以进行梯度传递和更新,可以在一定程度上避免神经元“死”掉的问题。
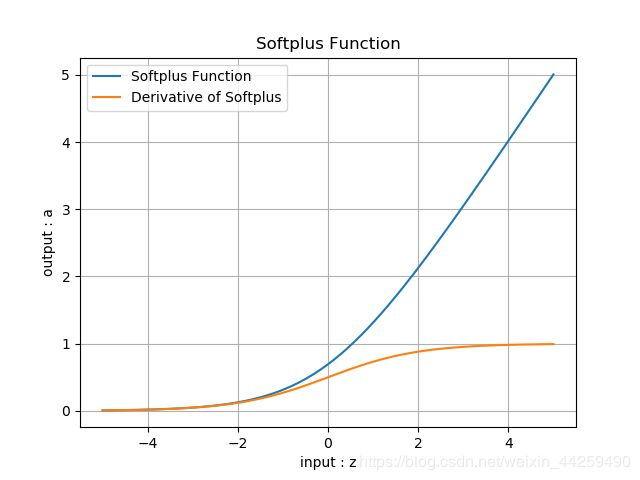
Softplus
公式:
a ( z ) = ln ( 1 + e z ) a(z) = \ln (1 + e^z) a(z)=ln(1+ez)
导数:
a ′ ( z ) = e z 1 + e z a'(z) = {e^z \over 1 + e^z} a′(z)=1+ezez
输入值域: [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
输出值域: [ 0 , ∞ ] [0,\infty] [0,∞]
导数值域: [ 0 , 1 ] [0,1] [0,1]
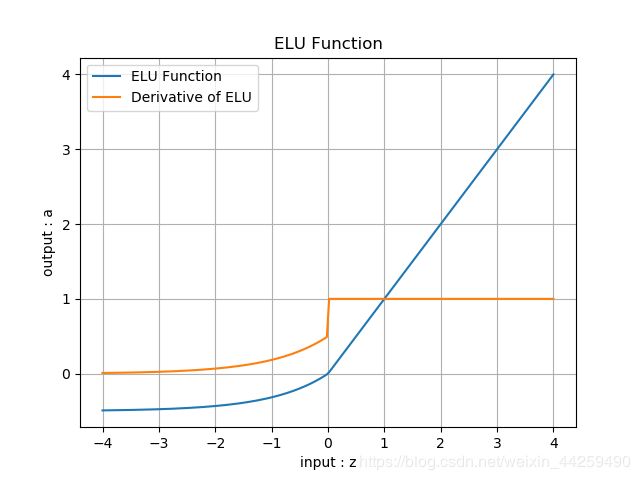
ELU
公式:
a ( z ) = { z z ≥ 0 α ( e z − 1 ) z < 0 a(z) = \begin{cases} z & z \geq 0 \ \alpha (e^z-1) & z < 0 \end{cases} a(z)={zz≥0 α(ez−1)z<0
导数:
a ′ ( z ) = { z 1 ≥ 0 α e z z < 0 a'(z) = \begin{cases} z & 1 \geq 0 \ \alpha e^z & z < 0 \end{cases} a′(z)={z1≥0 αezz<0
输入值域: [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
输出值域: [ − α , ∞ ] [-\alpha,\infty] [−α,∞]
导数值域: [ 0 , 1 ] [0,1] [0,1]
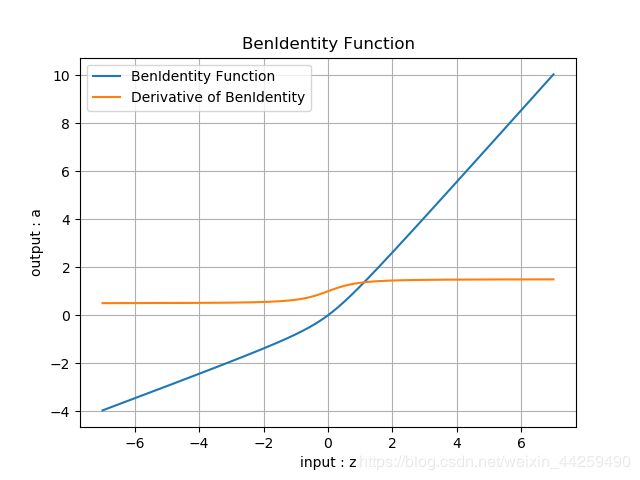
BenIdentity
公式:
a ( z ) = z 2 + 1 − 1 2 + z a(z) = {\sqrt{z^2 + 1} -1\over 2}+z a(z)=2z2+1−1+z
导数:
a ′ ( z ) = z 2 z 2 + 1 + 1 a'(z) = {z \over 2\sqrt{z^2+1}}+1 a′(z)=2z2+1z+1
输入值域: [ − ∞ , ∞ ] [-\infty, \infty] [−∞,∞]
输出值域: [ − ∞ , ∞ ] [-\infty,\infty] [−∞,∞]
导数值域: [ 0.5 , 1.5 ] [0.5,1.5] [0.5,1.5]
函数图像:
https://github.com/microsoft/ai-edu/blob/master/B-教学案例与实践/B6-神经网络基本原理简明教程/08.1-挤压型激活函数.md