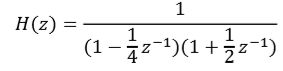【信号与系统学习笔记】【课程终章】—— 离散傅里叶变换的扩展：z 变换分析2

上文中，我们学习了《信号与系统》的第十章——z变换。这是我们学院教学大纲所要求的最后一章内容。因此，这将是本系列专栏的最后一篇课程笔记啦！但是文章却不止于此，平时关于信号与系统的一些思考我也会继续发上这个专栏的噢！那么下面我们先回顾一下关于z变换，我们之前都说了啥：

1. 常见的z变换对

【1】必须要记得的两个z变换对：$a^{n}u[n]$ 的z 变换为：$\frac{1}{1-a{z}^{-1}}$，ROC为：$|z|>|a|$
【2】$-a^{n}u[-n-1]$ （左边信号），它的z变换为：$\frac{1}{1-a{z}^{-1}}$，ROC为：$|z|<|a|$

2. ROC 的性质

另外，我们还学习了左边、右边、双边信号和他们的ROC所应该具有的特征；

3. z变换的性质

---

那么，本次博客我们将会探讨以下几点：1. z变换的ROC和系统性质之间的关系 2. 系统的框图描述 3. 单边z变换

一、z变换与系统的联系

1.1 z变换的ROC与系统因果性的关系

大家记忆：如果说一个系统，它的系统函数的z变换的ROC位于最外层极点的外面，同时ROC还包含了无穷远点时，那么这个系统就是因果的。 这里的"ROC还包含了无穷远点"，它的意思就是：$\infty$ 不能是 H(z) 的极点。那么什么时候$\infty$ 不是 H(z) 的极点呢？—— 如果 H(z) 表示成了多项式之比的形式，且分母项的阶次大于等于分子项的阶次时，$\infty$ 不是 H(z) 的极点，相反，此时$\infty$ 是 H(z) 的零点。

1.2 z变换的ROC与系统稳定性之间的关系

我们知道，一个系统要想是稳定的，在时域上需要满足下面这个条件：$$\sum _{n=-\infty }^{+\infty }h[n]<\infty$$

这不仅仅说明了系统函数绝对可和，他也说明了系统函数的傅里叶变换一定存在。 那么，到了z域，也是类似的，如果系统函数的z变换的ROC包含了单位圆，我们就可以判断这个系统是稳定的。

1.3 系统结构与H(z)的关系

同样地，我们目前所了解的系统基本结构包括——级联、并联和反馈。我们下面分别来看看：

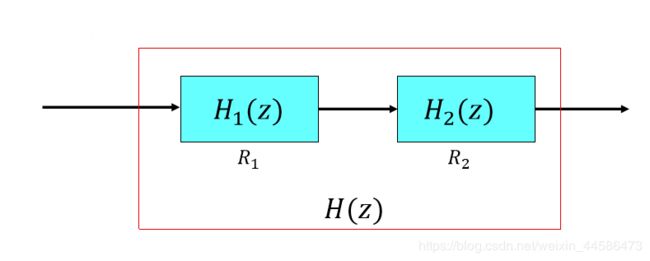
在时域中，系统级联我们用卷积来描述：$h_1[n]\ast h_2[n]$
在频域中，系统级联我们用乘积来描述：$H_1(e^{j\omega })H_2(e^{j\omega })$
那么在复数域里面，我们同样也是用乘积来描述：$H_1(z)H_2(z)$

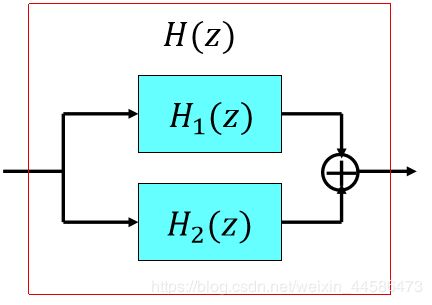
在时域中，系统级联我们用相加来描述：$h_1[n]+h_2[n]$
在频域中，系统级联我们也用相加来描述：$H_1(e^{j\omega })+H_2(e^{j\omega })$
那么在复数域里面，我们同样也是用相加来描述：$H_1(z)+H_2(z)$

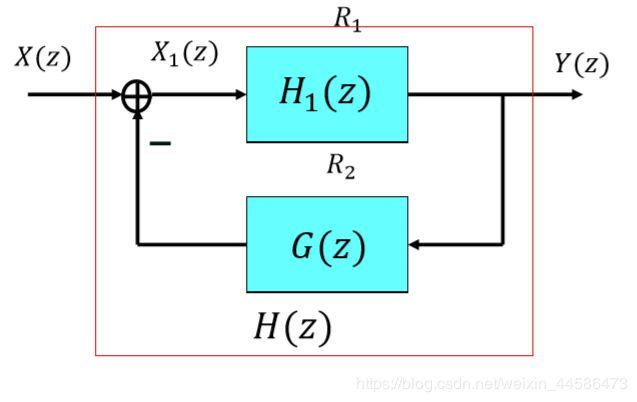
对于反馈系统，我们直接构造 $\frac{Y(z)}{X(z)}$ ，消除中间变量即可。我们来试试：
首先，反馈的输出我们知道是：$Y(z)G(z)$，那么就有：$X(z)-Y(z)G(z)=X_1(z)$，有因为：
$X_1(z)H_1(z)=Y(z)$，联立上面两个式子，将中间量 $X_1(z)$ 消掉即可。

二、系统的框图描述

我们知道，对于离散时间系统而言，常常用差分方程来描述。因此我们约定：在框图里面就只能用：加法器、乘以系数和$z^{-1}$（等价于延时一个单位时间）

另外框图也分为直接型框图、级联型框图和并联型框图。我们在考试时要按照题目要求画出对应的图。我们下面介绍一下；

分别画出下面这个系统函数

的直接型框图、级联型框图和并联型框图

对于初学者而言，也许需要先把差分方程给写出来：$$y[n]=\frac{1}{4}y[n-1]-\frac{1}{8}y[n-2]=x[n]$$
即：$$y[n]=x[n]-\frac{1}{4}y[n-1]+\frac{1}{8}y[n-2]$$
因此，我们就可以画出直接型：

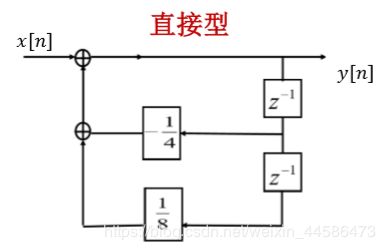
下面给大家支一招：直接型的通法：

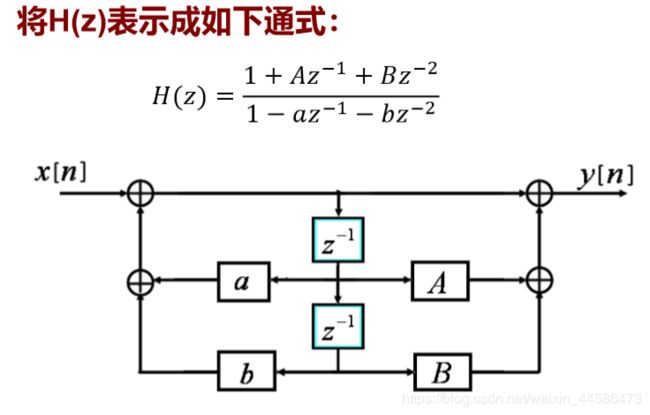
如果题目给出的多项式比，少了哪一项，我们就可以把哪一项的线给它抹去。

下面是级联型的画法：

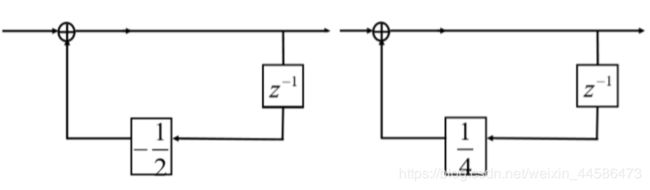
如果要改成并联型，则需要做部分分式展开，框图如下：

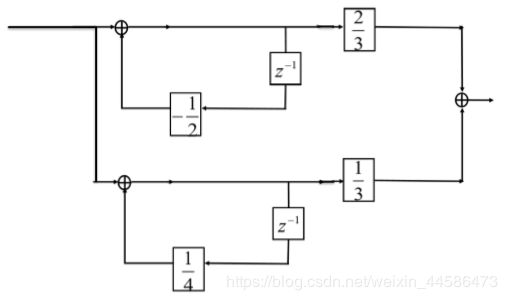
三、单边z变换

单边z变换，顾名思义就是求和区间是$[0,+\infty ]$。如果信号只是在 $[0,+\infty ]$ 有值，那么双边z变换和单边 z 变换的结果是一样的。如果信号在 $n<0$ 时还有值，那么两者的结果就不一样了。

另外值得注意的一点是单边z变换的时移特性：
【1】若 $x[n]$的单边z变换为：$X(z)$，那么$x[n-1]$ 的单边z变换为：$z^{-1}X(z)+x(-1)$、
【2】若 $x[n]$的单边z变换为：$X(z)$，那么$x[n+1]$ 的单边z变换为：$z^{1}X(z)+zx(0)$

根据单边z变换的这个性质，我们系统的输出往往就可以分为——零输入响应和零状态响应了。

终于归纳完啦！这一个学期由于疫情的影响变得非常特殊。天天坐在家里，对着博客的页面打字也是一件需要耐得住寂寞的事情哈哈。非常庆幸自己坚持了下来，没有在做前几次笔记之后就打退堂鼓。就因为这样才有了这一片博客的尾声。在此也对阅读我专栏的同学们说一声——加油！！未来可期！