决策树学习笔记——决策树建树原理之C4.5和C5.0以及CART建树原理（二）

决策树学习笔记——决策树建树原理之C4.5和C5.0以及CART建树原理（二）

在上一篇决策树学习笔记——决策树建树原理之ID3建树原理（一）.已经简单介绍了ID3算法的建树原理，以及附上了Python计算信息增益的代码。

C4.5原理

由ID3算法的原理知，ID3算法的弊端在于更倾向于选择水平数量较多的自变量，因为当自变量水平数量较多时，信息增益就越大，并且输入的自变量必须是分类型变量，而C4.5改变了ID3算法中的选择指标，将信息增益改为信息增益率。而且加入了对于自变量是连续性变量时的处理方法。

信息增益率

$B$为因变量，$A$为自变量，则ID3算法中，信息增益的数学表达式为：
$$Gain(A,B)=Entropy(A)-Entrop{y}_B(A)$$
而信息增率则是在信息增益的基础上除以自变量$B$的信息熵，数学表达式如下：
$$GainRate(A,B)=\frac{Gain(A,B)}{Entropy(B)}$$
选择规则也是跟ID3算法类似，信息增益率最大的，将作为首要变量建起第一层决策树。

C4.5对连续变量的计算原理

之前的原理，都只是针对名义变量（分类型变量）来说的，对于连续性变量，是不能直接计算信息增益或者信息增益率的，因此C4.5算法加入了处理连续变量的方式，使得连续变量也能计算信息增益和信息增益率。处理方式如下：
假设有$A_1$，$A_2$两个连续变量，在$A_1$中，有$a_1,a_2,...a_n$。则在建树之前，对变量$A_1$进行分箱处理，首先对变量$A_1$进行升序排序，则有$n-1$种分类方法，当然，对于同一水平下的，不需要切开（因为对于同一水平的因变量，将它们分割开来是不能提高信息增益率的），进行分割，分别和因变量计算信息增益，如此迭代下去，找出最大的信息增益率的那一次划分。之后，取那个划分方式的分割点，作为变量$A_1$的分箱方式。同理计算变量$A_2$的信息增益率，取最高信息增益率的变量作为首要变量，进入决策树的第一层。
例如有以下数据：

$A_1$	$A_2$	Y
50	15	0
55	10	0
60	80	1
65	70	1
70	20	1
75	13	0
80	78	0
85	32	0
90	36	0
95	78	1
100	29	0

则对于变量$a1$来说，切分点应该是$\le 55,>55$；$\le 70,>70$；$\le 90,>90$；$\le 95,>95$。

Python代码计算连续型变量信息增益率

利用Python自定义函数一个信息增益率的函数，我的代码可能有一些不足之处，望谅解。代码如下：

# 创建数据
data=[[50,55,60,65,70,75,80,85,90,95,100],[0,0,1,1,1,0,0,0,0,1,0]]
data=np.array(data)
data=pd.DataFrame(data.T)
data.columns=["a1","y"]
#信息熵
def Entropy_y(y):
    y=list(y)
    x_value = set(y)
    ent1=0.0
    for i in x_value:
        ent1=y.count(i)/len(y)*(-1)*np.log2(y.count(i)/len(y))+ent1
    return ent1
#连续型变量条件熵
def Entropy_x_y_con(y,x):
    a=[]
    ent=[]
    for i in range(len(y)-1):
        if y[i+1]!=y[i]:
            a.append(x[i])
    for i in a:
        sub_i=y[x<=i]
        sub_b=y[x>i]
        temp_ent1=Entropy_y(sub_i)
        temp_ent2=Entropy_y(sub_b)
        ent.append(temp_ent1*len(x[x<=i])/len(y)+temp_ent2*len(x[x>i])/len(y))
    return ent
#连续性变量的信息熵
def Entropy_x(y,x):
    aa=[]
    ent=[]
    for i in range(len(y)-1):
        if y[i+1]!=y[i]:
            aa.append(x[i])
    for j in aa:
        dd=np.sum(x<=j)
        ee=np.sum(x>j)
        sm=ee+dd
        ent.append(-(dd/sm*np.log2(dd/sm)+ee/sm*np.log2(ee/sm)))
    return ent
#连续变量的信息增益率
def GainRate(y,x):
    d=[]
    f=[]
    gg=[]
    for i in range(len(y)-1):
        if y[i+1]!=y[i]:
            d.append(x[i])
    for j in Entropy_x_y_con(y,x):
        f.append(Entropy_y(y)-j)
    for k in range(len(Entropy_x_y_con(y,x))):
        gg.append(f[k]/Entropy_x(y,x)[k])
        print("分割点为:",d[k],"则Gainrate is:",gg[k])

GainRate(y=data.y,x=data.a1)

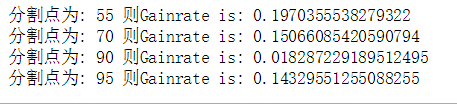
由图可知，当分割点为55的时候，信息增益率最大，同理计算变量$a2$的最大信息增益率，与$a1$作对比，选出信息增益率最大的自变量作为首要变量进入决策树第一层。
在名义变量中，信息增益率只计算一次，但是在连续性变量中，信息增益率可以重复计算，可以计算$n-1$次。

C5.0算法

C5.0是C4.5的改进版本，基础的算法是跟C4.5一样的，但是C5.0对以下地方进行的优化
1.增强了对大量数据处理的能力。
2.C5.0可以人为的加入客观规则
3.C5.0运行内存较小，C4.5需要几个G，而C5.0只需要几百mb。
4.运行速度比C4.5快很多倍。
5.C5.0加入了boosting提升算法，即通过构造多个C4.5算法，进而提升准确性，并且还可以加入惩罚项。
C5.0的boosting提升算法，被开发为工具包商业化，目前我还未找到有详细介绍其算法步骤和数学描述内容的相关资料。

CART算法

CART树是一个二叉树，即只能建立二叉树，对于多分类的的变量，需要将多分类变成二分类，形成超类，再进行相应的计算。
之前的ID3、C4.5、C5.0算法都只能做分类树，CART算法可以做分类树和回归树。CART算法的最优分割选择的标准不再是信息增益或信息增益率，而是gini系数。
CART与C4.5、C5.0类似的是，CART算法也可以处理连续性变量，处理方式与C4.5的处理方式类似，只是切分点有所不同，CART算法选取的切分点是相邻数值的中间值最为阈值，将连续性变量划分为两个类别，进而分别计算两个类别下的gini系数。gini系数越小，纯度越大，即划分得越好。
gini系数的数学表达式为：
$$gini(D)=1-\sum {\left(\frac{k_i}{n}\right)}^2$$
其中，$k_i$是因变量D中类别$i$的个数，$n$是变量D的总个数，即样本个数。
假设加入了自变量T，根据CART算法原理，则自变量T会将因变量D划分成两份，此处记为$D_1$，$D_2$，且$D_1$，$D_2$的个数分别为$n_1$，$n_2$，则划分后D的gini系数的数学表达式如下：
$$gin{i}_T(D)=\frac{n_1}{n_1+n_2}gini(D_1)+\frac{n_2}{n_1+n_2}gini(D_2)$$

案例

$A_1$	$A_2$	Y
50	白	0
55	黑	0
60	黑	1
65	黑	1
70	白	1
75	白	0
80	黑	0
85	白	0
90	白	0
95	白	1
100	白	0

使用Python分别定义计算名义变量、连续性变量的gini系数函数，代码及输出结果如下：

# 构建数据
data=[[50,55,60,65,70,75,80,85,90,95,100],["白","黑","黑","黑","白","白","黑","白","白","白","白"],[0,0,1,1,1,0,0,0,0,1,0]]
data=np.array(data)
data=pd.DataFrame(data.T)
data.columns=["a1","a2","y"]

#y的gini系数
def gini_y(y):
    cate_g=set(y)
    gini1=0.0
    for i in cate_g:
        gini1=-((np.sum(y==i)/len(y))**2)+gini1
    gini=1+gini1
    return gini
#名义变量的gini系数
def gini_class(x,y):
    cate_g=set(x)
    cate_g=list(cate_g)
    ginid_1=gini_y(y[x==cate_g[0]])
    ginid_2=gini_y(y[x==cate_g[1]])
    s_1=len(y[x==cate_g[0]])
    s_2=len(y[x==cate_g[1]])
    gini_split=(s_1/(s_1+s_2))*ginid_1+(s_2/(s_1+s_2))*ginid_2
    return gini_split
gini_class(x=data.a2,y=data.y)

#连续型变量的gini系数
import numpy as np
def gini_cont(x,y):
    sor=list(x)
    mean=[]
    gini_split_2=[]
    for i in range(len(sor)-1):
        mean.append((float(sor[i])+float(sor[i+1]))/2)
    for j in range(len(mean)):
        a=y[x<=str(mean[j])]
        b=y[x>str(mean[j])]
        s1=len(a)
        s2=len(b)
        ginit_1=gini_y(a)
        ginit_2=gini_y(b)
        gini_split_2.append((s1/(s1+s2))*ginit_1+(s2/(s1+s2))*ginit_2)
    gini_min=np.min(gini_split_2)
    return "最小的gini系数为：",gini_min,"对应的分割点为:",mean[gini_split_2.index(gini_min)]
gini_cont(x=data.a1,y=data.y)

由以上结果可知变量$a_1$，$a_2$不同的划分结果得出的最优gini系数不一样，选取最小的gini系数对应的变量，即$a1$变量最为首要变量进入决策树的第一层。