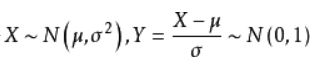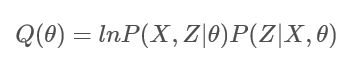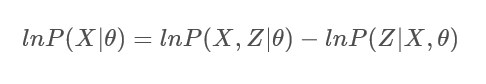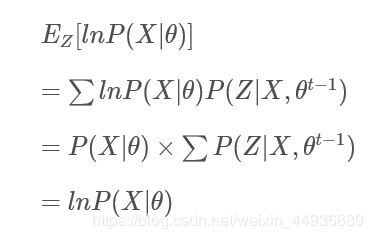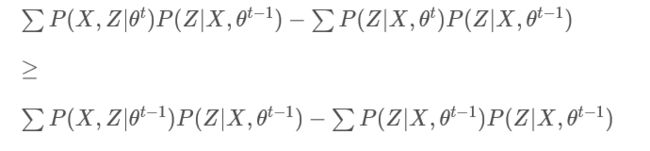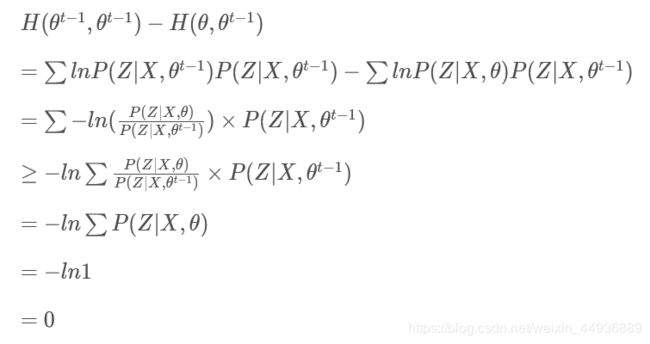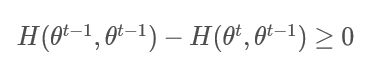【机器学习基础】EM算法详解及其收敛性证明
EM算法详解
- （一）单高斯模型
- 1.1 一维高斯分布：
- 1.2 多维高斯分布：
- （二）最大似然估计
- 2.1 最大似然估计的数学概念：
- 2.2 最大似然估计的基本步骤：
- 2.2.1 构造似然函数：
- 2.2.2 对数似然函数：
- 2.2.3 计算参数估计值：
- （三）混合高斯模型
- 3.1 单高斯模型的局限：
- 3.2 全概率公式：
- 3.3 混合高斯模型的概念：
- （四）最大似然估计的局限
- 4.1 混合模型的似然函数：
- 4.2 对数似然函数估计时的问题：
- （五）最大期望估计（EM算法）
- 5.1 EM算法的基本概念：
- 5.2 Q函数公式：
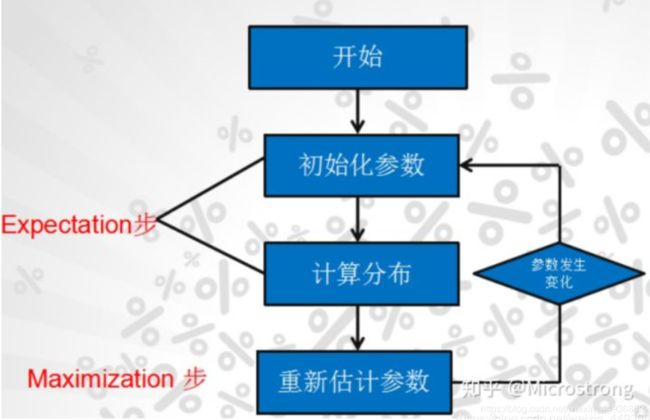
- 5.3 EM算法的基本步骤：
- 5.3.1 模型参数的初始化：
- 5.3.2 E-Step：
- 5.3.3 M-Step：
- （六）EM算法收敛性的证明
- 1. 证明的直观目标：
- 2. 推导和证明过程：
- 2.1 条件概率公式：
- 2.2 对两边求期望：
- 2.3 Q函数和H函数：
- 2.4 Jenson不等式：
- （七）EM算法的应用——视频背景分割：
- 7.1 论文地址：
- 7.2 检测效果：
- 7.3 原理详解及其实现：
（一）单高斯模型
1.1 一维高斯分布：
高斯分布（Gaussian Distribution）又叫正态分布（Normal Distribution），是一种常用的概率分布。
对于一组数据，其分布如图，我们可以用高斯模型去拟合这组数据的分布：
服从均值为 μ \mu μ、标准差为 σ \sigma σ的高斯分布在x点的概率密度为：
我们通常使用一个线性变换，将其转换成均值为0、方差为1的标准正态分布：
1.2 多维高斯分布：
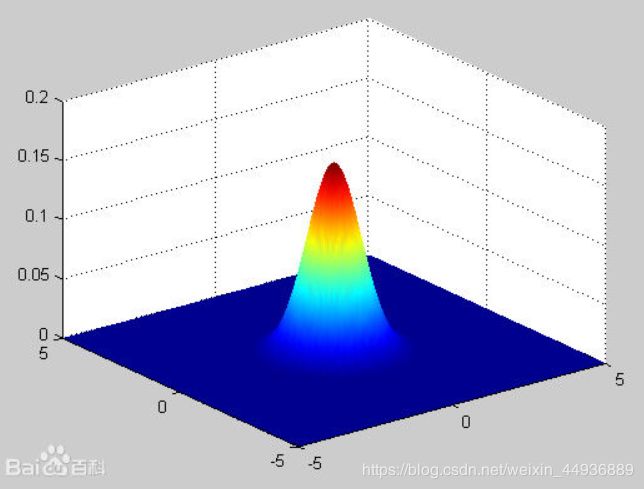
以二维高斯分布为例，我们现在判断的是一个多维向量（这里是二维）X = (x1, x2)，其分布为服从均值为 μ \mu μ1 μ \mu μ2、标准差为 σ \sigma σ1 σ \sigma σ2的高斯分布：
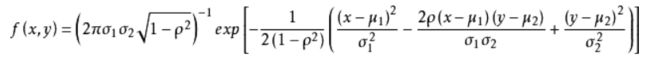
（二）最大似然估计
2.1 最大似然估计的数学概念：
假设我们手中有一个样本集X，X={ x1，x2，……，xN } 共N个样本，我们假设其符合均值为 μ \mu μ、标准差为 σ \sigma σ的高斯分布：
这时我们需要通过一定的方法去估计这个高斯分布的均值 μ \mu μ和标准差 σ \sigma σ，方法之一就是最大似然估计。
2.2 最大似然估计的基本步骤：
2.2.1 构造似然函数：
由于我们假设这个样本符合高斯分布（均值 μ \mu μ和标准差 σ \sigma σ未知，记为 θ \theta θ），那么X中的某个样本 x i x_{i} xi在参数 θ = { μ ， σ } \theta=\lbrace \mu，\sigma \rbrace θ={μ，σ}下取得相应的值的概率为 f ( x i ) f(x_{i}) f(xi)，记为 f ( x i ; θ ) f(x_{i} ; \theta) f(xi;θ);
我们构造一个函数 L ( θ ) L(\theta) L(θ)，称之为似然函数：
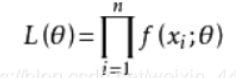
那么使L( θ \theta θ)最大的参数 θ \theta θ（注意xi均已知），就是我们的估计值；
2.2.2 对数似然函数：
然后对似然函数L( θ \theta θ)取对数，得到对数似然函数：
这里求对数的原因是我们下一步需要求偏导，这里使用对数将乘除转换成加减，便于计算；
2.2.3 计算参数估计值：
然后对对数似然函数求导，并令其为0（注意多个参数时分别求偏导）：
就得到了参数 θ \theta θ的估计值；
对于一维高斯分布：
（注意求得参数 θ \theta θ的时候需要先求 μ \mu μ，因为 σ \sigma σ的估计值中有 μ \mu μ）
（三）混合高斯模型
3.1 单高斯模型的局限：
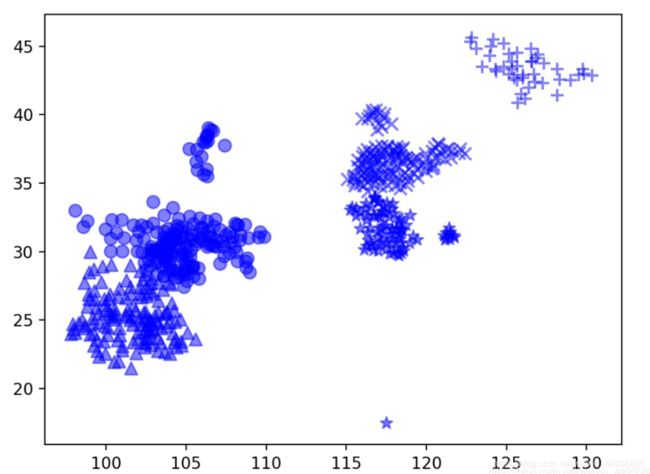
但是现实中往往我们得到的数据的分布并不均匀：
如果我们继续使用单个高斯模型去拟合这组数据，得到的结果可能是一个均值 μ \mu μ为所有x的均值、标准差 σ \sigma σ非常大的一个分布：
显然这并不能很好地拟合这组数据的分布，因为对于高斯分布，越往均值处（椭圆中心）数据分布应该越密集，但似乎这组数据有不同的概率中心，即这组数据可能分别属于不同的高斯分布；
这时候就需要混合高斯模型了。
3.2 全概率公式：
全概率公式为概率论中的重要公式，它将对一复杂事件A（取得x）的概率求解问题转化为了在不同情况下发生的简单事件的概率的求和问题；
3.3 混合高斯模型的概念：
复杂的数据往往是多峰的（如上图），这时我们就使用多个高斯分布来描述这样的数据分布，公式满足全概率公式：
其中：
- p ( x ) p(x) p(x) 是样本取得x值的概率；
- K K K 表示共有K个模型；
- p ( k ) p(k) p(k) 表示x属于第k个高斯模型的概率；
- p ( x ∣ k ) p(x|k) p(x∣k) 表示在第k个高斯模型下取得x的概率；
那么p(x)也等价为：
其中：
5. π \pi π k k k 是第k个高斯模型的权重；
6. μ \mu μ k k k 是第k个高斯模型的均值；
7. ε \varepsilon ε k k k 是第k个高斯模型的标准差；
此时K个模型组成的混合高斯模型的参数为：
θ \theta θ = { π \pi π1,……, π \pi πK-1, μ \mu μ1,……, μ \mu μK, ε \varepsilon ε1,……, ε \varepsilon ε K K K }
（注意这里由于 ∑ k = 1 K \sum_{k=1}^K ∑k=1K π \pi πk = 1，故参数 π \pi π的自由度为K-1）
（四）最大似然估计的局限
4.1 混合模型的似然函数：
这时我们再尝试用最大似然估计的方法来估计参数 θ \theta θ 的值：
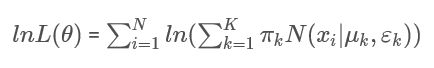
我们可以看到这里的对数似然函数中， l n ( ) ln() ln() 里面包含了求和项：
4.2 对数似然函数估计时的问题：
即使我们已经对似然函数取了对数，但是求出的偏导中各个参数的估计值相互关联，计算非常复杂；
这时我们就需要找一种方法，能够用相对简单的方式去估计或者去迭代趋近这个估计值；这种方法就叫做最大期望算法（Expectation-Maximization algorithm，简称EM算法）。
（五）最大期望估计（EM算法）
5.1 EM算法的基本概念：
EM算法的核心概念就是：
通过引入隐藏变量构造一个更为简单的函数（记为 Q Q Q函数），对 Q Q Q函数进行最大似然估计计算参数的估计值 θ \theta θ；
如果能够证明每次迭代时通过最大化 Q ( θ t − 1 ) Q(\theta^{t-1}) Q(θt−1)时得到的参数 θ \theta θ的新的估计值 θ t \theta^{t} θt满足：
那么第t次迭代的参数的估计值为：
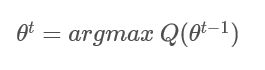
通过不断迭代，就可以最终得到收敛的参数 θ \theta θ，此时我们认为这个 θ \theta θ就是我们分布模型的参数的估计值。
5.2 Q函数公式：
我们构造如图所示的Q函数：
其中：
- X X X 是样本集， X = { x 1 , x 2 , … … , x N } X=\lbrace x_{1},x_{2},……,x_{N} \rbrace X={x1,x2,……,xN}；
- Z Z Z 是隐藏参数， Z = { z 1 , z 2 , … … , z N } Z=\lbrace z_{1},z_{2},……,z_{N}\rbrace Z={z1,z2,……,zN}，其中 z i = k z_{i}=k zi=k表示 x i x_{i} xi属于第k个高斯模型；
- θ \theta θ 是待估参数， θ = { μ 1 , … … , μ N , ε 1 , … … , ε N } \theta=\lbrace\mu_{1},……,\mu_{N},\varepsilon_{1},……,\varepsilon_{N}\rbrace θ={μ1,……,μN,ε1,……,εN}；
即，第t次迭代的结果为：
5.3 EM算法的基本步骤：
注：具体的公式推导会写在收敛性的证明里面；
5.3.1 模型参数的初始化：
这时我们明白了EM算法的基本原理，但是当我们开始第一次迭代的时候会发现一个很重要的问题：
- 我们需要知道 Z 0 = { z 0 , 1 , z 0 , 2 , … … , z 0 , N } Z^0=\lbrace z_{0,1},z_{0,2},……,z_{0,N}\rbrace Z0={z0,1,z0,2,……,z0,N}（z下标第一个数为迭代次数t），才能根据 Z Z Z写出函数 Q Q Q，并获得参数 θ \theta θ的估计值；
- 但是，同时我们也需要知道 θ 0 \theta^0 θ0的值，才能根据混合高斯模型的公式推导出样本X的分布属于哪一个单高斯模型，即 Z Z Z的值；
这样似乎我们就陷入了一个两难的境地；
但是由于我们知道，每次迭代得到的值 θ t \theta^{t} θt都越来越接近参数 θ \theta θ的估计值，因此我们不如在抽样之前先给每种样本依照经验赋予一个初始分布（即变量 θ 0 \theta^0 θ0），再依照分布求取隐藏变量 Z Z Z的期望，这样再开始不断迭代，就能得到最终的 θ \theta θ;
5.3.2 E-Step：
E-Step 指的是Exception步骤，即求取样本 X X X的隐藏变量 Z Z Z的期望 Z t − 1 Z^{t-1} Zt−1：
-
如果是第1次运行E-Step，使用初始化的高斯混合分布函数确定样本 X = { x 1 , x 2 , … , x N } X=\lbrace x_{1},x_{2},…,x_{N} \rbrace X={x1,x2,…,xN}属于的概率最大的分类，从而预估隐藏参数 Z 0 Z^{0} Z0；
-
如果是第 t t t次运行E-Step，则使用经过 t − 1 t-1 t−1次迭代、参数为 θ t − 1 \theta^{t-1} θt−1的高斯混合分布函数确定隐藏参数 Z t − 1 Z^{t-1} Zt−1。
5.3.3 M-Step：
M-step 指的是Maximization步骤，即求取混合模型的参数 θ t \theta^{t} θt：
通过最大化 Q ( θ t − 1 ) Q(\theta^{t-1}) Q(θt−1)，得到新的参数估计值 θ t \theta^t θt;
（六）EM算法收敛性的证明
1. 证明的直观目标：
我们的最终目标，是证明EM算法迭代足够多的次数得到的 θ t \theta^t θt，能够近似表示混合高斯模型的参数估计值 θ \theta θ，那就等价于证明每次迭代得到的 θ t \theta^t θt满足:
直观上理解就是，只要我们能够证明每次迭代的参数 θ t \theta^t θt，能够使的对数似然函数 l n L ( θ t ) lnL(\theta^{t}) lnL(θt)比上一次迭代的参数 l n L ( θ t − 1 ) lnL(\theta^{t-1}) lnL(θt−1)更大，那么我们认为经过足够多的次数的迭代，就可以使得 l n L ( θ ) lnL(\theta) lnL(θ)最大化；
此时的 θ t \theta^t θt就认为是参数 θ \theta θ的估计值；
2. 推导和证明过程：
2.1 条件概率公式：
对数似然函数（这里用概率 P P P表示样本 X X X的概率乘积），引入隐含变量 Z Z Z可以表示为：
即：
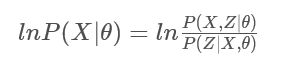
2.2 对两边求期望：
对上述等式两边在分布 Z Z Z下求其期望，得：
左边由于样本属于不同分布的概率之和 ∑ P ( Z ∣ X , θ t − 1 ) \sum P(Z|X,\theta^{t-1}) ∑P(Z∣X,θt−1)为1，可得：
右边同样可以得到：
此时有：
其中 l n P ( X ∣ θ ) lnP(X|\theta) lnP(X∣θ)就是对数似然函数；
到这一步我们就只需要证明：
即证明：
2.3 Q函数和H函数：
这时我们发现：
并构造 H H H函数：
此时证明的不等式转换为：
由于我们对 Q Q Q函数进行最大似然估计得到的 θ t \theta^t θt满足：
那么在 θ = θ t − 1 \theta=\theta^{t-1} θ=θt−1时：
这样我们只需要证明：
或者：
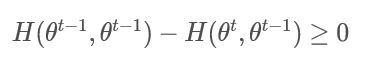
H ( θ t − 1 , θ t − 1 ) − H ( θ t , θ t − 1 ) ≥ 0 H(\theta^{t-1},\theta^{t-1})-H(\theta^{t},\theta^{t-1})\geq 0 H(θt−1,θt−1)−H(θt,θt−1)≥0
即可证明不等式：
2.4 Jenson不等式：
Jenson不等式表述为，如果函数 f f f是一个凸函数（注：有的地方叫凹函数，定义不尽相同，但都满足二次导数 f ′ ′ ≤ 0 f^{''}\leq0 f′′≤0），则满足：
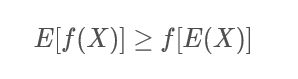
直观上描述为：函数值的期望大于期望的函数值；
这样我们就可以得到：
当 θ = θ t \theta=\theta^t θ=θt时：
至此证明完毕
（七）EM算法的应用——视频背景分割：
EM算法广泛应用于混合模型特别是混合高斯模型的参数估计，一种应用就是通过对视频中每个像素点进行建模，来实现对视频中的运动目标检测和背景分割；
7.1 论文地址：
《Effective Gaussian Mixture Learning for Video Background Subtraction》
7.2 检测效果：
7.3 原理详解及其实现：
可以看我的这篇博客：
【目标追踪】基于高斯混合学习的视频背景减法