Geom-GCN: Geometric Graph Convolutional Networks

作者: 纪厚业,北京邮电大学博士生,主要关注异质图神经网络及其应用.

Geom-GCN: Geometric Graph Convolutional Networks

知乎专栏对公式支持较好, 见 https://zhuanlan.zhihu.com/c_1158788280744173568

个人公众号 图与推荐

Introduction

图神经网络（Graph Neural Network）已经成为深度学习领域最热门的方向之一。作为经典的Message-passing模型，图神经网络通常包含两步：从邻居节点收集消息message，然后利用神经网络来更新节点表示。但是Message-passing模型有两个基础性的问题：

• 丢失了节点与其邻居间的结构信息。

  • 主要指拓扑模式相关的信息。

  • GNN的结构捕获能力已经有了相关论文。下图来自19ICLR GIN How Powerful are Graph Neural Networks

    

• 无法捕获节点之间的长距离依赖关系。

  • 大多数MPNNs仅仅聚合k跳内的节点邻居消息来更新节点表示。但是，图上两个节点可能具有相似的结构（社区中心、桥节点），即使他们的距离很远。
  • 可能的解法是将现有的GNN堆叠多层，但是这可能带来过平滑问题。

针对上述问题，本文提出了一种geometric aggregation scheme，其核心思想是：将节点映射为连续空间的一个向量（graph embedding），在隐空间查找邻居并进行聚合。

本文的主要贡献：

• 提出了一种geometric aggregation scheme，其可以同时在真实图结构/隐空间来聚合信息来克服MPNNs两个基础性缺陷。
• 提出了一种基于geometric aggregation scheme的图神经网络Geom-GCN。
• 实验验证了模型的效果。

Model

Geometric aggregation scheme

如下图所示，Geometric aggregation scheme主要包含3个部分：node embedding (panel A1-A3)，structural neighborhood (panel B) 和 bi-level aggregation (panel C)。

A1->A2： 利用graph embedding技术将图上的节点(如节点$v$)映射为隐空间一个向量表示${\mathbf{z}}_v$。

A2->B1：针对某一个节点$v$（参看B2中的红色节点）周围的一个子图，我们可以找到该节点的一些邻居$\mathcal{N}(v)=\left(\left\{N_g(v),N_s(v)\right\},\tau \right)$。

B2：圆形虚线（半径为$\rho$）内的节点代表了红色节点$v$在隐空间的邻居$N_s(v)=\left\{u|u\in V,d\left({\mathbf{z}}_u,{\mathbf{z}}_v\right)<\rho \right\}$；圆形虚线外的节点代表了节点在原始图上的真实邻居$N_g(v)=\{u|u\in V,(u,v)\in E\}$。既然节点已经表示为向量，那么不同节点之间就有相对关系。在B2的3x3网格内，不同节点相对于红色节点有9种相对位置关系$r_1,...,r_9$，关系映射函数为$\tau :\left({\mathbf{z}}_v,{\mathbf{z}}_u\right)\to r\in R$。

B3：基于Bi-level aggregation来聚合邻居$\mathcal{N}(v)$的信息并更新节点$v$的表示。

• Low-level aggregation $p$： 聚合节点$v$在某个关系$r$下的邻居的信息.这里用一个虚拟节点的概念来表示.

$$e_{(i,r)}^{v,l1}=p\left(\left\{{\mathbf{h}}_u^l|u\in N_i(v),\tau \left({\mathbf{z}}_v,{\mathbf{z}}_u\right)=r\right\}\right),\forall i\in \{g,s\},\forall r\in R$$

• High-level aggregation $q$: 聚合节点$v$在多种关系$R$下的邻居的信息.
  $${\mathbf{m}}_v^{l1}=\underset{i\in \{g,s\},r\in R}{q}\left(\left({\mathbf{e}}_{(i,r)}^{v,l1},(i,r)\right)\right)$$

• Non-linear transform: 非线性变化一下
  $${\mathbf{h}}_v^{l1}=\sigma \left({\mathbf{W}}_l\cdot {\mathbf{m}}_v^{l1}\right)$$
  其中,${\mathbf{h}}_v^l$是节点$v$在第l层GNN的表示.

这里本质上:先针对一种关系$r$来学习节点表示,然后再对多个关系下的表示进行融合.

Geom-GCN: An implementation of the scheme

这里将上一节中很抽象的Low-level aggregation $p$和High-level aggregation $q$以及关系映射函数$\tau$。给出了具体的形式:

关系映射函数$\tau$考虑了4种不同的位置关系.

Low-level aggregation $p$其实就是GCN中的平均操作.
$$e_{(i,r)}^{v,l1}=\sum _{u\in N_i(v)}\delta \left(\tau \left({\mathbf{z}}_v,{\mathbf{z}}_u\right),r\right)(\mathrm{deg}(v)\mathrm{deg}(u){)}^{\frac{1}{2}}{\mathbf{h}}_u^l,\forall i\in \{g,s\},\forall r\in R$$
High-level aggregation $q$本质就是拼接操作.
$${\mathbf{h}}_v^{l1}=\sigma \left(W_l\cdot \underset{i\in \{g,p\}}{\Vert }{\mathrm{ll}}_{r\in R}{\mathbf{e}}_{(i,r)}^{v,l1}\right)$$

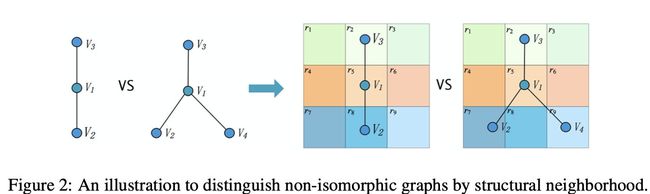
How to distinguish the non-isomorphic graphs once structural neighborhood

本文argue之前的工作没能较好的对结构信息进行描述.这里给了一个case study来说明Geom-GCN的优越性.

假设所有节点的特征都是$a$.针对节点$V_1$来说,其邻居分别为$\{V_2,V_3\}$和$\{V_2,V_3,V_4\}$. 假设采用mean或者maximum的aggregator.

• 之前的映射函数$f$, $Agg\{f(a),f(a)\}=Agg\{f(a),f(a),f(a)\}$.则两种结构无法区分.
• 本文的映射函数$f_i$, $Agg\{f_2(a),f_8(a)\}\ne Agg\{f_2(a),f_7(a),f_9(a)\}$, 则两种结构可以区分.

更多关于GNN表示能力的论文参见:19ICLR GIN How Powerful are Graph Neural Networks

Experiments

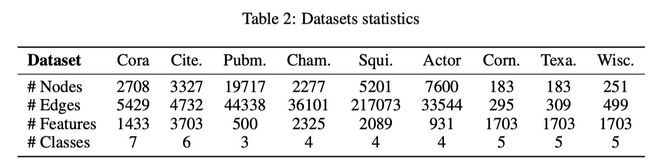
本文主要对比了GCN和GAT,数据集见下表:

不同数据集的homophily可以用下式衡量.

本文为Geom-GCN选取了3种graph embedding方法

• Isomap (Geom-GCN-I),
• Poincare embedding (Geom-GCN-P)
• struc2vec (GeomGCN-S).

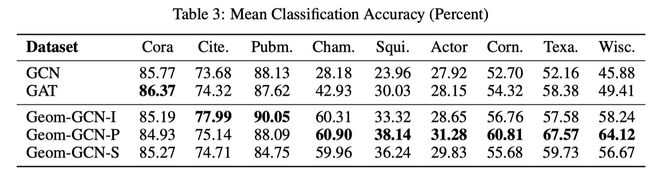
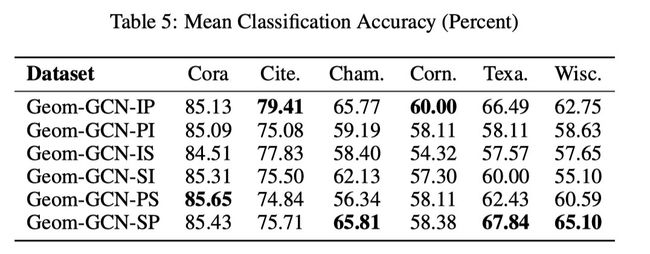
实验结果见下表:

作者又进一步测试了两个变种:

• 只用原始图上邻居,加上后缀-g. 如Geom-GCN-I-g
• 只用隐空间邻居,加上后缀-s. 如Geom-GCN-I-s

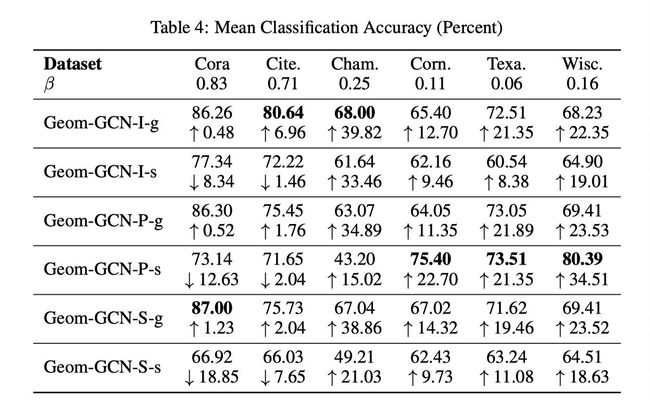
结果见下图:

可以看出:隐空间邻居对$\beta$较小的图贡献更大.

然后,作者测试了不同embedding方法在选取邻居上对实验结果的影响.

可以看出:这里并没有一个通用的较好embedding方法.需要根据数据集来设置,如何自动的找到最合适的embedding方法是一个feature work.

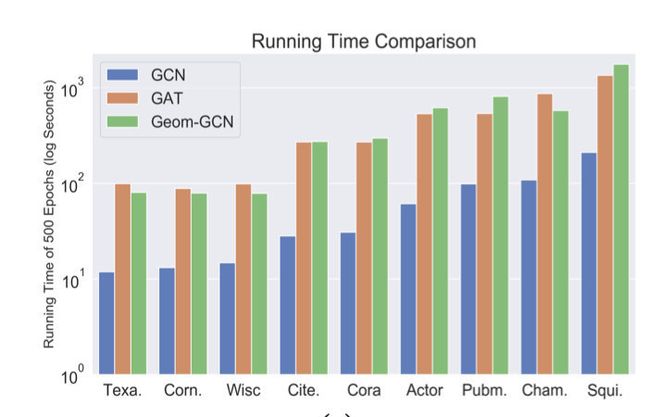
最后是时间复杂度分析.本文考虑了多种不同的关系,因此,Geom-GCN的时间复杂度是GCN的$2|R|$倍.另外,和GAT的实际运行时间相差无几,因为attention的计算通常很耗时.

Conclusion

本文针对MPNNs的两个基础性缺陷设计了Geom-GCN来更好的捕获结构信息和长距离依赖.实验结果验证了Geom-GCN的有效性.但是本文并不是一个end-to-end的框架.有很多地方需要手动选择设计.