综述 图神经网络时代的深度聚类
作者:纪厚业
单位:北京邮电大学
研究方向:图神经网络和推荐系统
文章目录
- Introduction
- Models
- 19IJCAI Attributed Graph Clustering: A Deep Attentional Embedding Approach
- Motivation
- Model
- 带有注意力机制的图自编码器
- 自训练聚类
- Experiment
- 20WWW Structural Deep Clustering Network
- Motivation
- Model
- DNN模块
- GCN模块
- 双重自监督模块
- Experiment
- 19IJCAI Attributed Graph Clustering via Adaptive Graph Convolution
- Motivation
- Model
- 谱域的图卷积
- 自适应k选择
- Experiment
- 20ArXiv Embedding Graph Auto-Encoder with Joint Clustering via Adjacency Sharing
- Motivation
- Model
- 图自编码器
- 联合聚类
- Experiment
- Conclusion
Introduction
聚类作为经典的无监督学习算法在数据挖掘/机器学习的发展历史中留下了不可磨灭的印记. 其中,经典的聚类算法K-Means也被选为数据挖掘十大经典算法. 随着深度学习的兴起,一些工作尝试将深度学习技术(如Autoencoder)引入到传统聚类算法中,也取得了不错的效果.
近些年,图神经网络已经成为深度学习领域最热门的方向之一, 也在推荐/自然语言处理/计算机视觉等很多领域得到了广泛的应用.
那么,能不能利用图神经网络强大的结构捕获能力来提升聚类算法的效果呢? 本文梳理总结了图神经网络赋能的深度聚类算法,供大家参考.
Models
19IJCAI Attributed Graph Clustering: A Deep Attentional Embedding Approach
Motivation
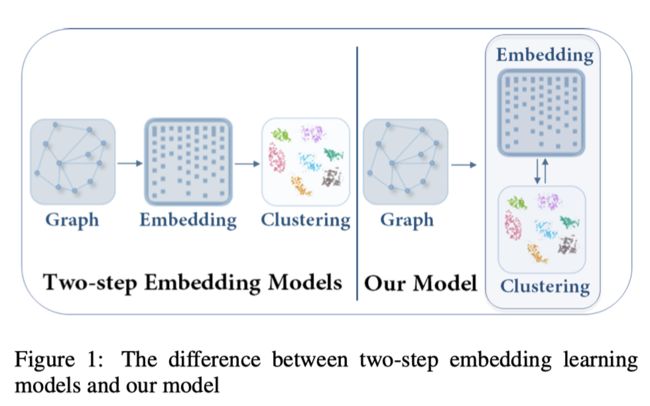
本文认为之前的深度聚类算法都是two-step的: 首先学习数据的特征表示embedding,然后基于特征表示进行数据聚类. 这样所学习的数据embedding并不是任务导向的. 那么,如果能够在学习embedding的过程中,针对聚类任务做一些针对性的设计,那么学习到的embedding自然可以实现更好的聚类.
针对上述问题,本文提出了一种聚类导向的深度算法Deep Attentional Embedded Graph Clustering (DAEGC). DAEGC一边通过图神经网络来学习节点表示,一边通过一种自训练的图聚类增强同一簇节点之间的内聚性.
下图清晰的展示two-step和本文所提出的DAEGC的差异.
Model
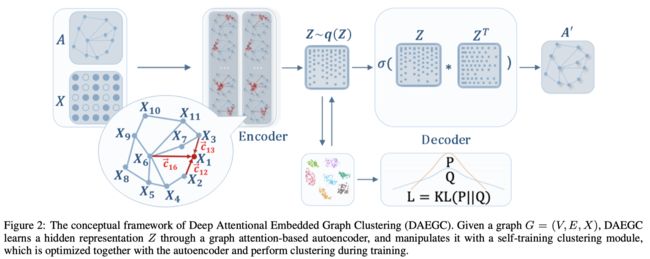
下图展示了DAEGC的模型框架
可以看出,整个DAEGC主要包含两大模块:带有注意力机制的图自编码器+自训练聚类.
带有注意力机制的图自编码器
这里就是经典的GAE架构:通过对邻居的聚合来学习节点表示,然后利用节点对的内积来重构原始网络结构. 比较有特色的部分就是结合注意力机制来学习邻居的权重, 这样可以更好的学习节点表示.
下式展示了融合注意力机制的GAE是如何聚合邻居信息来更新节点表示的.本质上就是对邻居的加权平均.
z i l + 1 = σ ( ∑ j ∈ N i α i j W z j l ) z_{i}^{l+1}=\sigma\left(\sum_{j \in N_{i}} \alpha_{i j} W z_{j}^{l}\right) zil+1=σ⎝⎛j∈Ni∑αijWzjl⎠⎞
其中, z i l , z i l + 1 z_{i}^{l},z_{i}^{l+1} zil,zil+1分别是聚合邻居信息前后的节点 i i i的表示, N i N_{i} Ni代表节点 i i i的邻居集合, α i j \alpha_{ij} αij表示了节点对 ( i , j ) (i,j) (i,j)之间的注意力权重.
有了节点表示后, GAE可以通过计算节点对的内积来重构原始网络结构,进而实现无监督的节点表示学习.
A ^ i j = sigmoid ( z i ⊤ z j ) \hat{A}_{i j}=\operatorname{sigmoid}\left(z_{i}^{\top} z_{j}\right) A^ij=sigmoid(zi⊤zj)
其中, A ^ i j \hat{A}_{i j} A^ij可以理解为节点对 ( i , j ) (i,j) (i,j)间存在边的概率.最后,通过经典的AE重构损失 L r = ∑ i = 1 n loss ( A i , j , A ^ i j ) L_{r}=\sum_{i=1}^{n} \operatorname{loss}\left(A_{i, j}, \hat{A}_{i j}\right) Lr=∑i=1nloss(Ai,j,A^ij)就可以对GAE进行训练.
自训练聚类
GAE所学习到的节点表示只是为了更好的重构网络结构,和聚类并没有直接联系.自训练聚类模块就是对GAE所学习到的embedding进行约束和整合,使其更适合于聚类任务. 假定聚类中为 μ u \mu_{u} μu, 那么节点 i i i属于某个类别的概率 q i u q_{i u} qiu, 如下式所示:
q i u = ( 1 + ∥ z i − μ u ∥ 2 ) − 1 ∑ k ( 1 + ∥ z i − μ k ∥ 2 ) − 1 q_{i u}=\frac{\left(1+\left\|z_{i}-\mu_{u}\right\|^{2}\right)^{-1}}{\sum_{k}\left(1+\left\|z_{i}-\mu_{k}\right\|^{2}\right)^{-1}} qiu=∑k(1+∥zi−μk∥2)−1(1+∥zi−μu∥2)−1
这里, q i u q_{i u} qiu可以看作是节点的分配的分布. 进一步的, 为了引入聚类信息来实现聚类导向的节点表示, 我们需要迫使每个节点与相应的聚类中心更近一些,以实现所谓的类内距离最小,类间距离最大.因此,我们定义了如下的目标分布:
p i u = q i u 2 / ∑ i q i u ∑ k ( q i k 2 / ∑ i q i k ) p_{i u}=\frac{q_{i u}^{2} / \sum_{i} q_{i u}}{\sum_{k}\left(q_{i k}^{2} / \sum_{i} q_{i k}\right)} piu=∑k(qik2/∑iqik)qiu2/∑iqiu
在目标分布中, 通过二次方 q i u q_{i u} qiu可以实现一种"强调"的效果(二次方后, 分布会变得更加尖锐,也更置信). 在训练过程中,分布 p p p实际起到了一种标签的效果. 最后,通过计算两个分布之间的KL散度,来实现互相约束,也就是所谓的自训练.
L c = K L ( P ∥ Q ) = ∑ i ∑ u p i u log p i u q i u L_{c}=K L(P \| Q)=\sum_{i} \sum_{u} p_{i u} \log \frac{p_{i u}}{q_{i u}} Lc=KL(P∥Q)=i∑u∑piulogqiupiu
综合起来,模型最终的损失函数为
L = L r + γ L c L=L_{r}+\gamma L_{c} L=Lr+γLc
节点 i i i的所处于的簇 s i \boldsymbol{s}_{i} si(也可以理解为其标签)可以通过下式计算:
s i = arg max u q i u \boldsymbol{s}_{i}=\arg \max _{u} q_{i u} si=argumaxqiu
Experiment
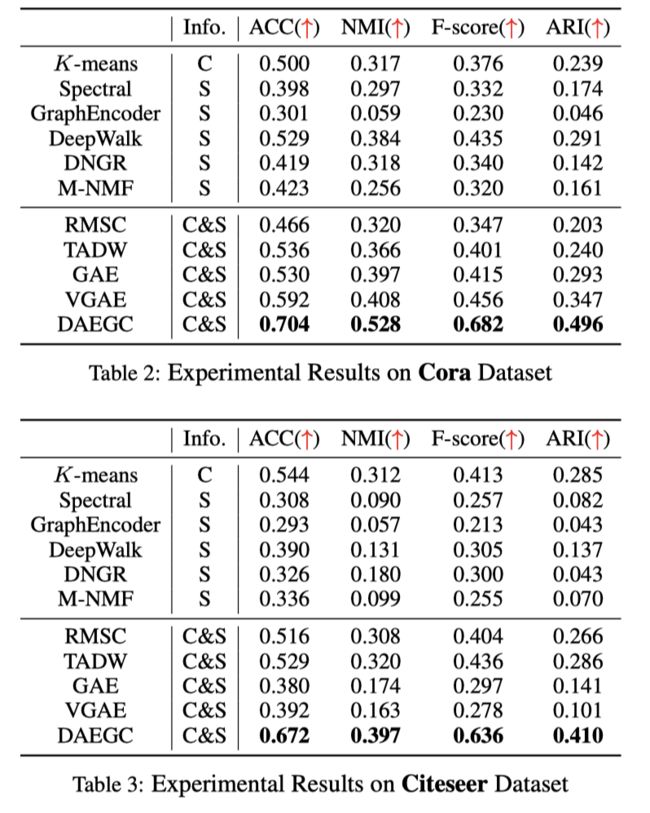
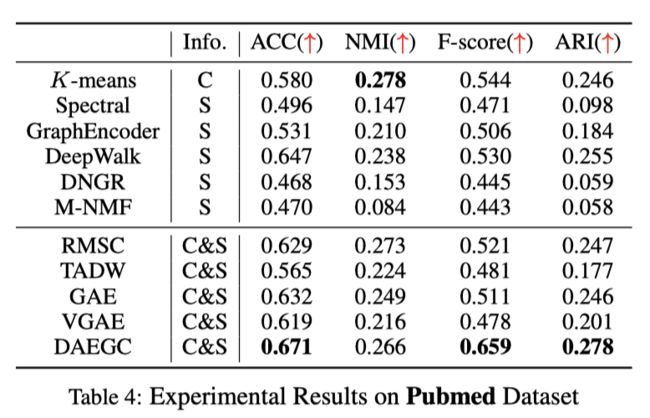
作者在3个数据集上进行了实现, DAEGC在大部分情况下都取得了最好的效果.
20WWW Structural Deep Clustering Network
Motivation
深度自编码器可以通过多层非线性编码来提取特征信息,而图神经网络可以聚合邻居信息来充分挖掘结构信息. 为了同时实现对特征的降维抽取和对结构信息的挖掘, 本文提出了Structural Deep Clustering Network (SDCN). 通过堆叠多层GNN, SDCN实现了对高阶结构信息的捕获. 同时,受益于自编码器和GNN的自监督, 这里的多层GNN并不会出现所谓的过平滑现象. 过平滑现象指的是,随着层数的增加,GNN所学习到的节点表示逐渐变得不可区分.
Model
在开始介绍模型之前,需要说明的是:如果数据集本身并没有图结构,作者将会通过计算节点之间的Top-K相似性利用KNN手动构建一张图. 下面是两种相似性计算方法: Heat Kernel和Dotp roduct
H e a t K e r n e l : S i j = e − ∥ x i − x j ∥ 2 t Heat\ Kernel:\mathbf{S}_{i j}=e^{-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{t}} Heat Kernel:Sij=e−t∥xi−xj∥2
D o t p r o d u c t : S i j = x j T x i Dot\ product: \mathbf{S}_{i j}=\mathbf{x}_{j}^{T} \mathbf{x}_{i} Dot product:Sij=xjTxi
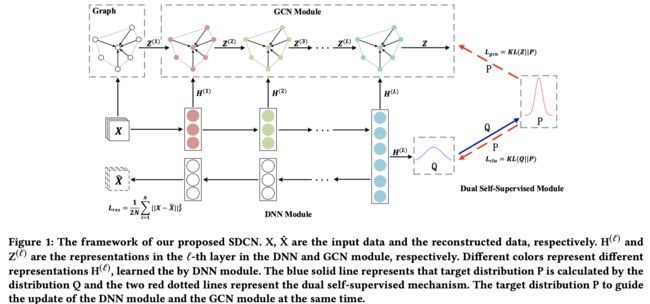
下图展示了整个SDCN的模型架构图. 可以看出,整个模型主要包含3个部分: GCN模块,DNN模块和双重自监督模块.
DNN模块
这里是一个经典的自编码器.编码器将输入 X \mathbf{X} X(也就是 H ( 0 ) \mathbf{H}^{(0)} H(0))通过神经网络编码为隐表示 H \mathbf{H} H; 解码器将隐表示 H \mathbf{H} H解码为 X ^ \hat{\mathbf{X}} X^(也就是 H ( L ) \mathbf{H}^{(L)} H(L)).
H ( ℓ ) = ϕ ( W e ( ℓ ) H ( ℓ − 1 ) + b e ( ℓ ) ) H ( ℓ ) = ϕ ( W d ( ℓ ) H ( ℓ − 1 ) + b d ( ℓ ) ) L r e s = 1 2 N ∥ X − X ^ ∥ F 2 \mathbf{H}^{(\ell)}=\phi\left(\mathbf{W}_{e}^{(\ell)} \mathbf{H}^{(\ell-1)}+\mathbf{b}_{e}^{(\ell)}\right) \\ \mathbf{H}^{(\ell)}=\phi\left(\mathbf{W}_{d}^{(\ell)} \mathbf{H}^{(\ell-1)}+\mathbf{b}_{d}^{(\ell)}\right)\\ \mathcal{L}_{r e s}=\frac{1}{2 N}\|\mathbf{X}-\hat{\mathbf{X}}\|_{F}^{2} H(ℓ)=ϕ(We(ℓ)H(ℓ−1)+be(ℓ))H(ℓ)=ϕ(Wd(ℓ)H(ℓ−1)+bd(ℓ))Lres=2N1∥X−X^∥F2
可以看出,通过重构loss和多层非线性映射, H ( ℓ ) \mathbf{H}^{(\ell)} H(ℓ)可以较好的反映节点的特征信息.
GCN模块
另一方面, GCN可以聚合邻居信息来更新节点表示,其更新过程如下:
Z ( ℓ ) = ϕ ( D ~ − 1 2 A ~ D ~ − 1 2 Z ( ℓ − 1 ) W ( ℓ − 1 ) ) \mathbf{Z}^{(\ell)}=\phi\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{Z}^{(\ell-1)} \mathbf{W}^{(\ell-1)}\right) Z(ℓ)=ϕ(D −21A D −21Z(ℓ−1)W(ℓ−1))
其中, Z ( ℓ ) \mathbf{Z}^{(\ell)} Z(ℓ)是第 ℓ \ell ℓ层GCN学习到的表示, A ~ = A + I \widetilde{\mathbf{A}}=\mathbf{A}+\mathbf{I} A =A+I是带有自联的邻接矩阵, D ~ i i = ∑ j A ~ i j \widetilde{\mathbf{D}}_{i i}=\sum_{j} \widetilde{\mathbf{A}}_{\mathbf{i j}} D ii=∑jA ij.
截止到目前为止都是一些常规的DNN和GCN.接下来就是SDCN的特色部分: 第 ℓ \ell ℓ层最终表示 Z ~ ( ℓ − 1 ) \widetilde{\mathbf{Z}}^{(\ell-1)} Z (ℓ−1)实际上混合了初始GCN表示 Z ( ℓ − 1 ) \mathbf{Z}^{(\ell-1)} Z(ℓ−1)和DNN的编码表示 H ( ℓ − 1 ) \mathbf{H}^{(\ell-1)} H(ℓ−1).
Z ~ ( ℓ − 1 ) = ( 1 − ϵ ) Z ( ℓ − 1 ) + ϵ H ( ℓ − 1 ) \widetilde{\mathbf{Z}}^{(\ell-1)}=(1-\epsilon) \mathbf{Z}^{(\ell-1)}+\epsilon \mathbf{H}^{(\ell-1)} Z (ℓ−1)=(1−ϵ)Z(ℓ−1)+ϵH(ℓ−1)
可以看出,在这一步,作者将GNN和DNN联系了起来.第L层的最终表示可以进一步映射为一个类别概率,
Z = softmax ( D ~ − 1 2 A ~ D ~ − 1 2 Z ( L ) W ( L ) ) Z=\operatorname{softmax}\left(\widetilde{\mathbf{D}}^{-\frac{1}{2}} \widetilde{\mathbf{A}} \widetilde{\mathbf{D}}^{-\frac{1}{2}} \mathbf{Z}^{(L)} \mathbf{W}^{(L)}\right) Z=softmax(D −21A D −21Z(L)W(L))
其中, z i j ∈ Z z_{ij}\in Z zij∈Z 可以看做是节点 i i i属于类别 j j j的概率, Z Z Z其实是一个指示了节点处于不同类别的概率分布.
双重自监督模块
最后是一个双重自监督模块,其作用体现在两个方面: (1)通过GCN部分和DNN部分的互相监督可以实现模型的无监督学习. (2)通过引入聚类信息来更好的学习任务导向的节点表示.与上一篇19IJCAI Attributed Graph Clustering: A Deep Attentional Embedding Approach类似, SDCN也设计了两个分布. 这里不再赘述,详见上一篇的解读.
节点的类别分布为:
q i j = ( 1 + ∥ h i − μ j ∥ 2 / v ) − v + 1 2 ∑ j ′ ( 1 + ∥ h i − μ j ′ ∥ 2 / v ) − v + 1 2 q_{i j}=\frac{\left(1+\left\|\mathbf{h}_{i}-\boldsymbol{\mu}_{j}\right\|^{2} / v\right)^{-\frac{v+1}{2}}}{\sum_{j^{\prime}}\left(1+\left\|\mathbf{h}_{i}-\boldsymbol{\mu}_{j^{\prime}}\right\|^{2} / v\right)^{-\frac{v+1}{2}}} qij=∑j′(1+∥∥hi−μj′∥∥2/v)−2v+1(1+∥∥hi−μj∥∥2/v)−2v+1
目标分布为:
p i j = q i j 2 / f j ∑ j ′ q i j ′ 2 / f j ′ p_{i j}=\frac{q_{i j}^{2} / f_{j}}{\sum_{j^{\prime}} q_{i j^{\prime}}^{2} / f_{j^{\prime}}} pij=∑j′qij′2/fj′qij2/fj
同样的,也是最小化两个分布之间的KL散度:
L c l u = K L ( P ∥ Q ) = ∑ i ∑ j p i j log p i j q i j \mathcal{L}_{c l u}=K L(P \| Q)=\sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} Lclu=KL(P∥Q)=i∑j∑pijlogqijpij
这里,我们可以将 p i j p_{i j} pij视为标签来对GCN模块进行监督.
L g c n = K L ( P ∥ Z ) = ∑ i ∑ j p i j log p i j z i j \mathcal{L}_{g c n}=K L(P \| Z)=\sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{z_{i j}} Lgcn=KL(P∥Z)=i∑j∑pijlogzijpij
总的来说, 分布 P P P起到了一个桥接的作用,将DNN所学到的表示和GCN所学习到的表示进行约束.
模型完整损失函数如下:
L = L r e s + α L c l u + β L g c n \mathcal{L}=\mathcal{L}_{r e s}+\alpha \mathcal{L}_{c l u}+\beta \mathcal{L}_{g c n} L=Lres+αLclu+βLgcn
节点 i i i的标签可以通过下式计算:
r i = arg max j z i j r_{i}=\underset{j}{\arg \max } z_{i j} ri=jargmaxzij
Experiment
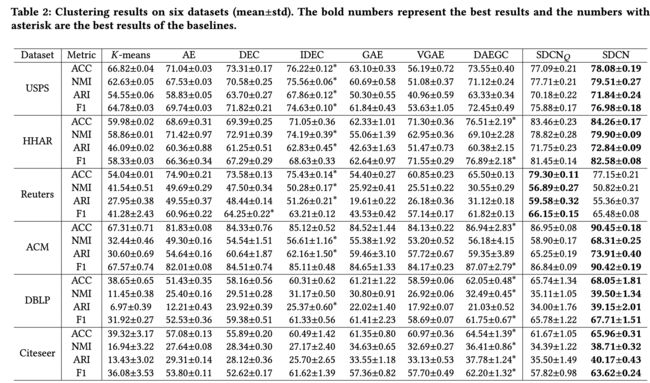
作者在6个数据集上做了大量的有效性实验. 可以看出, SDCN在所有数据集上都取得了大幅的提升.
比较有意思的实验是模型层数实验,如下图所示.可以看出,随着层数的增加,模型的效果会有大幅度的提升,并没有出现过平滑现象.
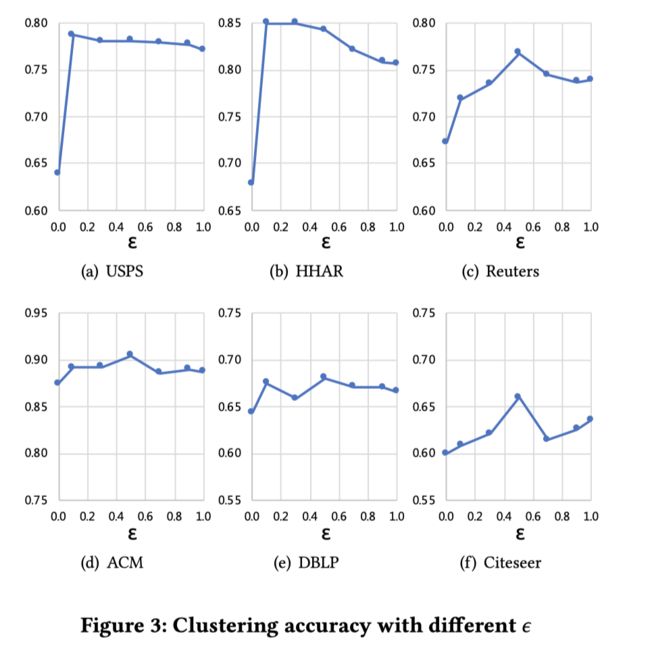
除此之外,作者还测试了不同的混合系数 ϵ \epsilon ϵ对模型效果的影响.
19IJCAI Attributed Graph Clustering via Adaptive Graph Convolution
Motivation
与上一篇SDCN相似,本文也利用了高阶结构信息(多层GNN)来提升聚类的效果.尽管这两篇非常相似,它们也是有一些差异的: (1) 本文所提出的AGC是从图信号处理谱图理论的角度来理解GNN并增强了聚类效果; (2) 本文所涉及的AGC可以自适应的选择高阶信息的阶数,而SDCN则需要手动指定超参数.
Model
谱域的图卷积
这里首先简单回顾一下谱域的图卷积:
f ‾ = G f = U p ( Λ ) U − 1 ⋅ U z = ∑ q = 1 n p ( λ q ) z q u q \overline{\boldsymbol{f}}=G \boldsymbol{f}=U p(\Lambda) U^{-1} \cdot U \boldsymbol{z}=\sum_{q=1}^{n} p\left(\lambda_{q}\right) z_{q} \boldsymbol{u}_{q} f=Gf=Up(Λ)U−1⋅Uz=q=1∑np(λq)zquq
其中, p ( Λ ) p(\Lambda) p(Λ)是一个频响函数,可以对 Λ \Lambda Λ中的值(也就是特征值)进行放缩, f ‾ , f \overline{\boldsymbol{f}}, \boldsymbol{f} f,f分别是经过图滤波器 G G G卷积前后的图信号.
f = U z = ∑ q = 1 n z q u q \boldsymbol{f}=U \boldsymbol{z}=\sum_{q=1}^{n} z_{q} \boldsymbol{u}_{q} f=Uz=q=1∑nzquq
这里, f \boldsymbol{f} f可以看做一组基信号的加权, 而这组基是由拉普拉斯矩阵$ L_s$分解得到的,
L s = U Λ U − 1 L_s=U \Lambda U^{-1} Ls=UΛU−1
其中, U = [ u 1 , ⋯ , u n ] U=\left[\boldsymbol{u}_{1}, \cdots, \boldsymbol{u}_{n}\right] U=[u1,⋯,un]代表 n n n个基向量, Λ = diag ( λ 1 , ⋯ , λ n ) \Lambda=\operatorname{diag}\left(\lambda_{1}, \cdots, \lambda_{n}\right) Λ=diag(λ1,⋯,λn)是一个对角阵, λ q \lambda_{q} λq的大小可以反映基向量 u q \boldsymbol{u}_{q} uq的平滑程度.
Ω ( u q ) = 1 2 ∑ ( v i , v j ) ∈ E a i j ∥ u q ( i ) d i − u q ( j ) d j ∥ 2 2 = u q ⊤ L s u q = λ q \begin{array}{l} \Omega\left(\boldsymbol{u}_{q}\right)=\frac{1}{2} \sum_{\left(v_{i}, v_{j}\right) \in \mathcal{E}} a_{i j}\left\|\frac{\boldsymbol{u}_{q}(i)}{\sqrt{d_{i}}}-\frac{\boldsymbol{u}_{q}(j)}{\sqrt{d_{j}}}\right\|_{2}^{2} \\ =\boldsymbol{u}_{q}^{\top} L_{s} \boldsymbol{u}_{q}=\lambda_{q}\end{array} Ω(uq)=21∑(vi,vj)∈Eaij∥∥∥∥diuq(i)−djuq(j)∥∥∥∥22=uq⊤Lsuq=λq
为什么这里需要涉及到"平滑"这个概念呢? 图上的"平滑"程度反映了相邻节点的相似程度.图上的高频意味着不平滑,特征值大; 图上的低频意味着平滑,特征值小.
那么在一组基中, 相对平滑的图信号实际上是有利于聚类的.因为聚类的目的是把相似的节点放到一起.
如何实现对低频信号的筛选(也就是对高频信号的抑制)呢? 其实很简单,我们只要想办法将较大特征进行压缩. 回想上面的频响函数 p ( Λ ) p(\Lambda) p(Λ)的作用, 我们可以设计恰当的 p p p来实现我们的目的
p ( λ q ) = 1 − 1 2 λ q p\left(\lambda_{q}\right)=1-\frac{1}{2} \lambda_{q} p(λq)=1−21λq
很明显, λ q \lambda_q λq越大, p ( λ q ) p\left(\lambda_{q}\right) p(λq)越小. 相应的图滤波 G G G可以写作:
G = U p ( Λ ) U − 1 = U ( I − 1 2 Λ ) U − 1 = I − 1 2 L s G=U p(\Lambda) U^{-1}=U\left(I-\frac{1}{2} \Lambda\right) U^{-1}=I-\frac{1}{2} L_{s} G=Up(Λ)U−1=U(I−21Λ)U−1=I−21Ls
一阶图卷积可以写作:
X ˉ = ( I − 1 2 L s ) X \bar{X}=\left(I-\frac{1}{2} L_{s}\right) X Xˉ=(I−21Ls)X
那么,k阶图卷积也呼之欲出,
X ˉ = ( I − 1 2 L s ) k X p ( λ q ) = ( 1 − 1 2 λ q ) k \bar{X}=\left(I-\frac{1}{2} L_{s}\right)^{k} X \\ p\left(\lambda_{q}\right)=\left(1-\frac{1}{2} \lambda_{q}\right)^{k} Xˉ=(I−21Ls)kXp(λq)=(1−21λq)k
到这里,也就可以聚合k阶邻居来学习节点表示了,也就是所谓的k阶图卷积.同时注意,卷积过程中抑制了高频信号,更多的低频信号(更符合聚类要求)被捕获了.
自适应k选择
现在还剩一个问题需要解决,图卷积的k阶该如何确定?
这里作者用了一个启发式的方法:逐渐增加k, 当类内距离开始变小时,停止搜索. 内类距离如下所示
i n t r a ( C ) = 1 ∣ C ∣ ∑ C ∈ C 1 ∣ C ∣ ( ∣ C ∣ − 1 ) ∑ v i , v j ∈ C ∥ x ˉ i − x ˉ j ∥ 2 i n t r a(\mathcal{C})=\frac{1}{|\mathcal{C}|} \sum_{C \in \mathcal{C}} \frac{1}{|C|(|C|-1)} \sum_{v_{i}, v_{j} \in C}\left\|\bar{x}_{i}-\bar{x}_{j}\right\|_{2} intra(C)=∣C∣1C∈C∑∣C∣(∣C∣−1)1vi,vj∈C∑∥xˉi−xˉj∥2
可以看出,这里k的选择也是比较符合聚类的要求(类内距离最小,类间距离最大).
Experiment
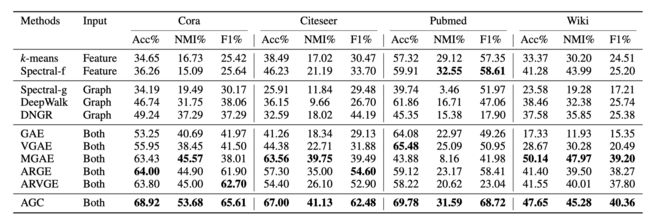
作者在4个经典数据集上进行了实验.总的来说,AGC的效果还是不错的.
20ArXiv Embedding Graph Auto-Encoder with Joint Clustering via Adjacency Sharing
Motivation
本文与之前几篇的类似,也是用GNN来学习适合于聚类任务的节点表示. 比较特别的是,本文同时考虑了K-Mean聚类和谱聚类来实现更好的聚类.
Model
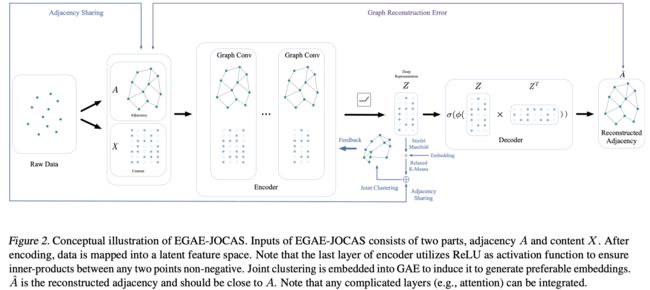
下图展示了本文所提出的Embedding Graph Auto-Encoder with JOint Clustering via Adjacency Sharing (EGAE-JOCAS)的整体框架.
图自编码器
首先,作者利用图卷积神经网络来学习节点的表示 Z Z Z, 然后利用节点表示来尝试重构原始图结构.
A ^ = σ ( ϕ ( Z Z T ) ) \hat{A}=\sigma\left(\phi\left(Z Z^{T}\right)\right) \\ A^=σ(ϕ(ZZT))
略有不同的是,作者这里对 Z Z T Z Z^{T} ZZT做了一个非线性变换.
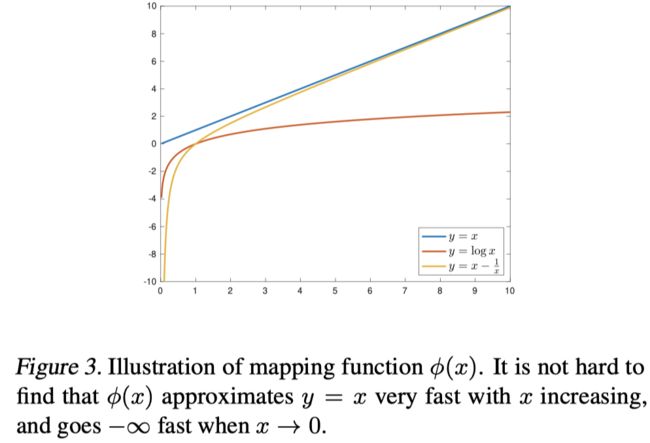
ϕ ( x ) = x − 1 x \phi(x)=x-\frac{1}{x} ϕ(x)=x−x1
作者认为 ϕ ( x ) \phi(x) ϕ(x)(函数曲线见下图)可以更好的对节点对的内积进行映射.在 x x x较大的时候, ϕ ( x ) \phi(x) ϕ(x)可以更好的逼近 y = x y=x y=x.
联合聚类
联合聚类的公式如下图所示,
min G T G = I ∥ X − F G T ∥ F 2 + γ tr ( G T L G ) \min _{G^{T} G=I}\left\|X-F G^{T}\right\|_{F}^{2}+\gamma \operatorname{tr}\left(G^{T} L G\right) GTG=Imin∥∥X−FGT∥∥F2+γtr(GTLG)
第一项是K-Mean聚类,其中 G G G是一个指示器, 实际上反映了节点属于不同簇的概率.
第二项是谱聚类,直观的理解就是,相近的节点应该属于相同的簇.回顾上一篇的"平滑程度",可以发现它们有异曲同工之妙.
Ω ( u q ) = u q ⊤ L s u q \begin{array}{l} \Omega\left(\boldsymbol{u}_{q}\right)=\boldsymbol{u}_{q}^{\top} L_{s} \boldsymbol{u}_{q}\end{array} Ω(uq)=uq⊤Lsuq
联合之前GAE的重构损失,EGAE-JOCAS最终的目标函数为:
min A ^ , Z , F , G T G = I J ( A ^ , A ) + α ( ∥ Z − F G T ∥ F 2 + γ tr ( G T L G ) ) \min _{\hat{A}, Z, F, G^{T} G=I} J(\hat{A}, A)+\alpha\left(\left\|Z-F G^{T}\right\|_{F}^{2}+\gamma \operatorname{tr}\left(G^{T} L G\right)\right) A^,Z,F,GTG=IminJ(A^,A)+α(∥∥Z−FGT∥∥F2+γtr(GTLG))
Experiment
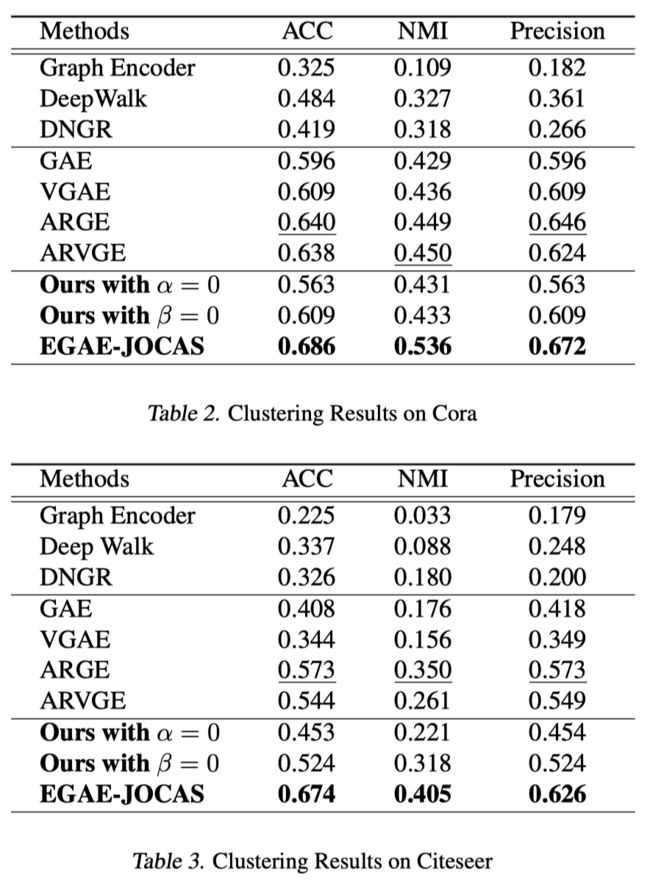
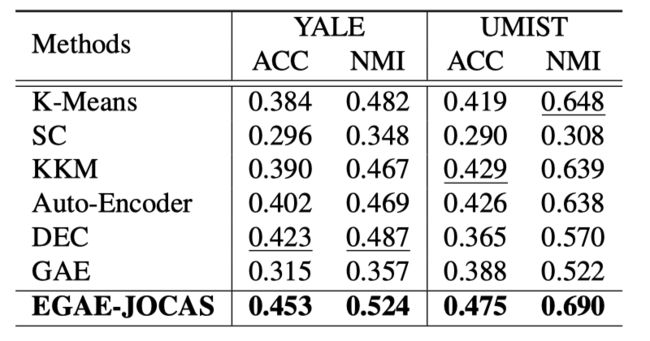
最后,作者在四个数据集上进行了实验. 总的来说,EGAE-JOCAS在所有数据集上都取得了明显的提升.
Conclusion
聚类是机器学习/数据挖掘的一个基础性问题.从传统聚类到深度聚类以及现在图神经网络赋能的聚类, 各种各样的聚类算层出不穷,也在很多领域得到了广泛的应用.考虑到图神经网络对结构信息的捕获能力,在涉及到群体结构的聚类任务上,本文所介绍的聚类算法应该会取得更大的提升.