DGL官方教程--图分类
Note:
Click here to download the full example code
Graph Classification Tutorial
Author: Mufei Li, Minjie Wang, Zheng Zhang.
在本教程中,您将学习如何使用DGL批处理多个大小和形状可变的图形。 本教程还演示了为简单的图分类任务训练图神经网络。
图分类是生物信息学,化学信息学,社会网络分析,城市计算和网络安全等许多领域应用的重要问题。 将图神经网络应用于此问题是最近流行的方法。 这可以在以下研究参考文献中看到: Ying et al., 2018, Cangea et al., 2018, Knyazev et al., 2018, Bianchi et al., 2019, Liao et al., 2019, Gao et al., 2019)。
Simple graph classification task
在本教程中,您将学习如何使用DGL执行批处理图分类。 示例任务目标是对此处显示的八种拓扑进行分类。
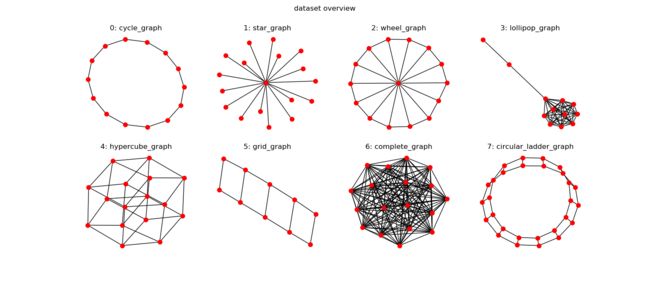
在DGL中实现data.MiniGCDataset数据。 数据集具有八种不同类型的图,每个类别具有相同数量的图样本。
from dgl.data import MiniGCDataset
import matplotlib.pyplot as plt
import networkx as nx
# A dataset with 80 samples, each graph is
# of size [10, 20]
dataset = MiniGCDataset(80, 10, 20)
graph, label = dataset[0]
fig, ax = plt.subplots()
nx.draw(graph.to_networkx(), ax=ax)
ax.set_title('Class: {:d}'.format(label))
plt.show()
Form a graph mini-batch
为了有效地训练神经网络,通常的做法是将多个样本一起批处理以形成一个小批处理。 批量分配固定形状的张量输入很常见。 例如,批处理两个大小为28 x 28的图像得到的张量形状为2 x 28 x28。相比之下,批处理图形输入有两个挑战:
- 图是稀疏的
- 图可以具有各种长度。 例如,节点和边的数量。
为了解决这个问题,DGL提供了dgl.batch()API。 它利用了这样的思想:可以将一批图视为具有许多不相连的相连组件的大型图。 下面是给出总体思路的可视化视图。

定义下面的collect函数,该函数使用一个给定的图片列表和一直相对应的标记形成一个mini-batch。
import dgl
def collate(samples):
# The input `samples` is a list of pairs
# (graph, label).
graphs, labels = map(list, zip(*samples))
batched_graph = dgl.batch(graphs)
return batched_graph, torch.tensor(labels)
dgl.batch()的返回类型仍然是图形。 同样,一批张量仍然是张量。 这意味着适用于一个图的任何代码都可立即用于一批图。 更重要的是,由于DGL并行处理所有节点和边缘上的消息,因此大大提高了效率。
Graph classifier
图形分类如下进行:

从一批图形中,执行消息传递和图形卷积,以使节点与其他节点通信。 消息传递后,根据节点(和边)属性为图表表示计算张量。 此步骤可能称为读出或汇总。 最后,将图形表示输入到分类器 g g g中以预测图形标签。
Graph convolution
图卷积操作与图卷积网络(GCN)基本上相同。 要了解更多信息,请参见GCN教程)。 唯一的区别是我们使用
h v ( l + 1 ) = ReLU ( b ( l ) + 1 ∣ N ( v ) ∣ ∑ u ∈ N ( v ) h u ( l ) W ( l ) ) h_{v}^{(l+1)} = \text{ReLU}\left(b^{(l)}+\frac{1}{|\mathcal{N}(v)|}\sum_{u\in\mathcal{N}(v)}h_{u}^{(l)}W^{(l)}\right) hv(l+1)=ReLU⎝⎛b(l)+∣N(v)∣1u∈N(v)∑hu(l)W(l)⎠⎞
替代了
h v ( l + 1 ) = ReLU ( b ( l ) + ∑ u ∈ N ( v ) h u ( l ) W ( l ) ) h_{v}^{(l+1)} = \text{ReLU}\left(b^{(l)}+\sum_{u\in\mathcal{N}(v)}h_{u}^{(l)}W^{(l)}\right) hv(l+1)=ReLU⎝⎛b(l)+u∈N(v)∑hu(l)W(l)⎠⎞
用平均值代替求和是为了平衡不同程度的节点。 这为该实验提供了更好的性能。
在数据集初始化中添加的自边缘允许您在取平均值时包括原始节点特征 h v ( l ) h_{v}^{(l)} hv(l)。
import dgl.function as fn
import torch
import torch.nn as nn
# 发送节点特征h的信息.
msg = fn.copy_src(src='h', out='m')
def reduce(nodes):
"""对所有相邻节点特征hu取平均值,并用它覆盖原始节点特征。"""
accum = torch.mean(nodes.mailbox['m'], 1)
return {'h': accum}
class NodeApplyModule(nn.Module):
"""使用ReLU(Whv+b)更新节点的特征hv."""
def __init__(self, in_feats, out_feats, activation):
super(NodeApplyModule, self).__init__()
self.linear = nn.Linear(in_feats, out_feats)
self.activation = activation
def forward(self, node):
h = self.linear(node.data['h'])
h = self.activation(h)
return {'h' : h}
class GCN(nn.Module):
def __init__(self, in_feats, out_feats, activation):
super(GCN, self).__init__()
self.apply_mod = NodeApplyModule(in_feats, out_feats, activation)
def forward(self, g, feature):
# 初始化h节点特征
g.ndata['h'] = feature
g.update_all(msg, reduce)
g.apply_nodes(func=self.apply_mod)
return g.ndata.pop('h')
Readout and classification
对于此演示,请将初始节点特征视为其度。 经过两轮图卷积后,通过对批处理中每个图的所有节点特征求平均值来执行图读出。
h g = 1 ∣ V ∣ ∑ v ∈ V h v h_g=\frac{1}{|\mathcal{V}|}\sum_{v\in\mathcal{V}}h_{v} hg=∣V∣1v∈V∑hv
在DGL中,dgl.mean_nodes()可处理一批可变大小的图形的此任务。 然后,将图形表示形式馈入具有一个线性层的分类器中,以获得pre-softmax logits。
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self, in_dim, hidden_dim, n_classes):
super(Classifier, self).__init__()
self.layers = nn.ModuleList([
GCN(in_dim, hidden_dim, F.relu),
GCN(hidden_dim, hidden_dim, F.relu)])
self.classify = nn.Linear(hidden_dim, n_classes)
def forward(self, g):
# 对于无向图,in_degree与out_degree相同。
h = g.in_degrees().view(-1, 1).float()
for conv in self.layers:
h = conv(g, h)
g.ndata['h'] = h
hg = dgl.mean_nodes(g, 'h')
return self.classify(hg)
Setup and training
创建包含10到20个节点的400个图形的综合数据集。 320张图构成训练集,而80张图构成测试集。
import torch.optim as optim
from torch.utils.data import DataLoader
# Create training and test sets.
trainset = MiniGCDataset(320, 10, 20)
testset = MiniGCDataset(80, 10, 20)
# Use PyTorch's DataLoader and the collate function
# defined before.
data_loader = DataLoader(trainset, batch_size=32, shuffle=True,
collate_fn=collate)
# Create model
model = Classifier(1, 256, trainset.num_classes)
loss_func = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)
model.train()
epoch_losses = []
for epoch in range(80):
epoch_loss = 0
for iter, (bg, label) in enumerate(data_loader):
prediction = model(bg)
loss = loss_func(prediction, label)
optimizer.zero_grad()
loss.backward()
optimizer.step()
epoch_loss += loss.detach().item()
epoch_loss /= (iter + 1)
print('Epoch {}, loss {:.4f}'.format(epoch, epoch_loss))
epoch_losses.append(epoch_loss)
Out:
Epoch 0, loss 2.0744
Epoch 1, loss 1.9880
Epoch 2, loss 1.9160
Epoch 3, loss 1.8144
Epoch 4, loss 1.7113
Epoch 5, loss 1.6263
Epoch 6, loss 1.5470
Epoch 7, loss 1.4899
Epoch 8, loss 1.4006
Epoch 9, loss 1.3282
Epoch 10, loss 1.2855
Epoch 11, loss 1.2143
Epoch 12, loss 1.1741
Epoch 13, loss 1.1528
Epoch 14, loss 1.1222
Epoch 15, loss 1.0702
Epoch 16, loss 1.0186
Epoch 17, loss 0.9897
Epoch 18, loss 0.9511
Epoch 19, loss 0.9401
Epoch 20, loss 0.9237
Epoch 21, loss 0.8890
Epoch 22, loss 0.8684
Epoch 23, loss 0.8634
Epoch 24, loss 0.8439
Epoch 25, loss 0.8617
Epoch 26, loss 0.8358
Epoch 27, loss 0.8125
Epoch 28, loss 0.7969
Epoch 29, loss 0.7825
Epoch 30, loss 0.7848
Epoch 31, loss 0.7588
Epoch 32, loss 0.7611
Epoch 33, loss 0.7410
Epoch 34, loss 0.7363
Epoch 35, loss 0.7259
Epoch 36, loss 0.7275
Epoch 37, loss 0.7067
Epoch 38, loss 0.7123
Epoch 39, loss 0.7041
Epoch 40, loss 0.6913
Epoch 41, loss 0.6950
Epoch 42, loss 0.7057
Epoch 43, loss 0.6905
Epoch 44, loss 0.6792
Epoch 45, loss 0.6564
Epoch 46, loss 0.6581
Epoch 47, loss 0.6522
Epoch 48, loss 0.6677
Epoch 49, loss 0.6617
Epoch 50, loss 0.6743
Epoch 51, loss 0.6706
Epoch 52, loss 0.6749
Epoch 53, loss 0.6402
Epoch 54, loss 0.6449
Epoch 55, loss 0.6470
Epoch 56, loss 0.6384
Epoch 57, loss 0.6003
Epoch 58, loss 0.6411
Epoch 59, loss 0.6144
Epoch 60, loss 0.6248
Epoch 61, loss 0.6192
Epoch 62, loss 0.6015
Epoch 63, loss 0.5879
Epoch 64, loss 0.5878
Epoch 65, loss 0.5694
Epoch 66, loss 0.5668
Epoch 67, loss 0.5765
Epoch 68, loss 0.5895
Epoch 69, loss 0.5819
Epoch 70, loss 0.5663
Epoch 71, loss 0.5822
Epoch 72, loss 0.5422
Epoch 73, loss 0.5726
Epoch 74, loss 0.5460
Epoch 75, loss 0.5430
Epoch 76, loss 0.5285
Epoch 77, loss 0.5383
Epoch 78, loss 0.5483
Epoch 79, loss 0.5399
训练的学习曲线如下所示。
plt.title('cross entropy averaged over minibatches')
plt.plot(epoch_losses)
plt.show()
在创建的测试集上评估训练后的模型。 要部署该教程,请限制运行时间,以使其比下面打印的精度更高(80%〜90%)。
model.eval()
# Convert a list of tuples to two lists
test_X, test_Y = map(list, zip(*testset))
test_bg = dgl.batch(test_X)
test_Y = torch.tensor(test_Y).float().view(-1, 1)
probs_Y = torch.softmax(model(test_bg), 1)
sampled_Y = torch.multinomial(probs_Y, 1)
argmax_Y = torch.max(probs_Y, 1)[1].view(-1, 1)
print('Accuracy of sampled predictions on the test set: {:.4f}%'.format(
(test_Y == sampled_Y.float()).sum().item() / len(test_Y) * 100))
print('Accuracy of argmax predictions on the test set: {:4f}%'.format(
(test_Y == argmax_Y.float()).sum().item() / len(test_Y) * 100))
Out:
Accuracy of sampled predictions on the test set: 67.5000%
Accuracy of argmax predictions on the test set: 75.000000%
此处的动画绘制了受过训练的模型预测正确图形类型的概率。
为了了解经过训练的模型学习到的节点和图形表示,我们使用t-SNE进行降维和可视化。

顶部的两个小图分别显示了一层和两层图卷积后的节点表示。 底部的图以图形表示形式将图形的softmax预登录可视化。
虽然可视化效果确实提示了节点功能的某些聚类效果,但您不会期望得到理想的结果。 节点度对于这些节点特征是确定的。 分离后图形功能得到改善。
What’s next?
使用图神经网络进行图分类仍然是一个新领域。 它正在等待人们带来更多激动人心的发现。 这项工作需要将不同的图映射到不同的嵌入,同时在嵌入空间中保留它们的结构相似性。 要了解更多信息,请参阅图神经网络有多强大? 在2019年国际学习代表大会上发表的研究论文。
有关批处理图处理的更多示例,请参见以下内容:
- Tree LSTM 和 Deep Generative Models of Graphs的教程
- Junction Tree VAE的示例实现
Total running time of the script: ( 0 minutes 27.221 seconds)
下载代码:4_batch.py
下载代码:4_batch.ipynb