Matlab绘图方法整理(超完整版)
文章目录
- 使用Matlab绘图
- 二维作图
- 其它形式下的二维曲线图
- 三维作图
- 三维曲线
- 三维曲面
- 图形修饰辅助操作
- 基础绘图指令
- 图形标注函数
- 图形修饰处理
- 视点处理
- 色彩处理
- 图形的裁剪处理
- 其它
- 总结
使用Matlab绘图
- 图像是结果的一种可视化表现,它能直观的体现你的结果,并且能体现你获得结果的准确性,在当前的大数据时代,在做数据分析的时候,将其可视化可以直观多维的展示数据,可以让人们更好的发现并且记住数据的特征,因此很多时候掌握一些绘图方法是非常重要的,而使用MATLAB可以非常简单的进行绘图(当然还有很多其它工具可供使用),下文是我所了解的一些基本绘图方法的整理,其中很多很多内容非常基础,希望对你能有些帮助。
二维作图
二维图像是我们在学习过程中经常会接触到的图像,比如在做数学题目时随手画出的一个正弦曲线,这个图像往往是我们根据它的函数做出来的,事实确是这样,在我们学习过程中画出来的每一个图像几乎都是函数,反过来说,每一个函数都对应着它自己的图像,我们能画出来的二维图像往往是一个一元函数即二元方程,在Matlab中做二维图像也是这样,我们根据一个函数来画出它的图像,不过要注意的一点是,在Matlab画图的过程中,它并不认识你给出的那个函数,它要做的仅仅是把你给出的函数上的点连成线而已。
- plot和fplot
在Matlab里面做二维图像最基础也是最常用的两个函数:plot()和fplot()函数,其中,plot的经常使用的方法有下面三种:
one
plot(x)
twoplot(x,y,参数)
threeplot(x1,y1,x2,y2,...,xn,yn)
首先,第一种方法里面若x为一维数组,则作出的图像是以其数组长度为横坐标,间隔为1,以数组中的具体值为纵坐标的。而其也可以为复数变量,如下:
y = [5,10,15,20]
z = [100,200,300,400]
x =y+z*i
//这里的x经过此定义将会被认为是一个复数变量
//图像将会以实部即y为横坐标,虚部即z为纵坐标作图
对于第二种形式就更好理解了,往往其中的x、y都为一维数组,其实y也就是x对应的函数值,后边的参数用于指定曲线的线形、颜色和数据点标记,如下:
x = [0:0.01:10]
y = sin(x)
plot(x,y,'-r*')
可以看到,x是一个长度为1001的一维数组,y是和x等长的在sin(x)上的一维数组,后边的-r*分别为曲线线性、颜色、数据点标记,其中参数的一些具体属性如下表所示:
| 线形 | 颜色 | 数据点标记 |
|---|---|---|
'-' : 实线 |
'k' : 黑色 |
* : 星号 |
':' : 虚线 |
b : 蓝色 |
o : 圆圈 |
'-.' : 点划线 |
c : 蓝绿色 |
s : 方块 |
'--' : 双划线 |
g : 绿色 |
p : 五角星 |
m : 洋红色 |
^ : 朝上三角符号 |
|
r : 红色 |
X : 叉 |
|
w : 白色 |
+ : + |
|
y : 黄色 |
d : 菱形 |
|
v : 朝下三角符号 |
||
< : 朝左三角符号 |
||
> : 朝右三角符号 |
||
H : 六角形 |
这些就是基本的绘图参数指令,搭配使用效果更佳。关于参数的使用是在每种方法中都可以添加,三种常用示例只是简单示例。关于第三种使用方法,意思是把n个图像做出在一个窗口中,同时也少敲了几个plot,当然,如果你想把代码分开写也可以,只需要加上hold on命令就行了,关于它后文会有介绍。
而关于fplot,其基本使用方法如下:
one
fplot(f,lims,参数)
twofplot(funx,funy,tlims,参数)
在第一种方法中,f代表一个函数,通常采用函数句柄的形式。lims为x轴的取值范围,用二元向量[xmin,xmax]描述,默认值为[-5,5]。参数定义与plot函数相同。例如使用fplot函数绘制sin(x)图像如下:
fplot(@(x)sin(x),[0,10],'-r')
在第二种方法中,funx、funy代表函数,通常采用函数句柄的形式。tlims为参数函数funx和funy的自变量的取值范围,用二元向量[tmin,tmax]描述。如绘制参数方程(x=tsint,y=tcost)曲线如下:
fplot(@(t)t.*sin(t),@(t)t.*cos(t),[0,10*pi],'-r')
其它形式下的二维曲线图
上文举例说明了最基础最常用的两个做二维曲线的函数,实际上,二维图形的种类还有很多,不光只有一根线构成的曲线图,还有各种统计图、坐标图等等,相应的在Matlab中也有画它们图形的方法,下面是其它几种图形作图方法(非全部):
- 对数坐标图
semilogx(x1,y1,'参数',x2,y2,'参数'...)
semilogy(x1,y1,'参数,x2,y2','参数'...)
loglog(x1,y1,'参数',x2,y2,'参数'...)
其中,semilogx函数x轴为常用对数刻度,y轴为线性刻度;semilogy函数x轴为线性刻度,y轴为常用对数刻度;loglog函数x轴和y轴均采用常用对数刻度。
- 极坐标图
polar(theta,rho,'参数')
其中,theta为极角,rho为极径,参数内容与plot相同。
- 条形图
bar(y,style)
bar(x,y,style)
x = [2018,2019,2020]
y = [10,20,30,40,50;
10,20,30,40,50;
10,20,30,40,50];
bar(x,y)
第一个,参数y是数据,选项style用于指定分组排列模式,模式有两种供选择,分别为:'grouped':簇状分组,'stacked':堆积分组。
第二个,x存储横坐标,y存储数据,y的行数必须与向量x的长度相同。选项style用于指定分组排列模式。
具体效果请自行练习查看。
- 直方图
hist(y)
hist(y,x)
其中,y是要统计的数据,x用于指定区间的划分方式。若x是标量,则统计区间均分成x个小区间;若x是向量,则向量x中的每一个数指定分组中心值,元素的个数为数据分组数。x缺省时,默认按10个等分区间进行统计。
rose(theta[],x)
其中,参数theta用于确定每一区间与原点的角度,选项x用于指定区间的划分方式。
- 面积类图形
pie(x,explode)
其中,参数x存储待统计数据,选项explode控制图块的显示模式。使用如下,可以试着改下参数或者help一下看看。
score = [10,25,3,18,41]
ex = [0,0,0,0,1]
pie(score,ex)
- 散点类图形
scatter(x,y,选项,'filled')
其中,x、y用于定位数据点,选项用于指定线型、颜色、数据点标记。如果数据点标记是封闭图形,可以用选项’filled’指定填充数据点标记。该选项省略时,数据点是空心的。
一颗心:
t = 0:pi/50:2*pi
x = 16*sin(t).^3
y = 13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t)
scatter(x,y,'rd','filled')
- 矢量类图形
quiver(x,y,u,v)
其中,(x,y)指定矢量起点,(u,v)指定矢量终点。x、y、u、v是同样大小的向量或同型矩阵,若省略x、y,则在x-y平面上均匀取若干个作为起点。
已知向量A、B,求A+B,并用矢量图表示。
A = [4,5]; B = [-10,0]; C = A+B;
hold on
quiver(0,0,A(1),A(2));
quiver(0,0,B(1),B(2));
quiver(0,0,C(1),C(2));
text(A(1),A(2),'A');text(B(1),B(2),'B');
text(C(1),C(2),'C')
axis([-12,6,-1,6])
grid on
- 进阶:双Y轴绘图
plotyy()
示例代码:
x = [0:0.01:20]
y1 = 200*exp(-0.05*x).*sin(x)
y2 = 0.8*exp(-0.5*x).*sin(10*x)
plotyy(x,y1,y2)
三维作图
在上文的二维作图示例中我们可以知道二维作图的基本方法,而有时候二维的图形满足不了我们的需要,这个时候就需要做一些三维图像了,而三维图像里边除了包含曲线作图之外还包含曲面作图。
三维曲线
在二维曲线作图里边我们主要使用的函数是plot和fplot函数,而在三维曲线作图里面我们使用的是plot3和fplot3函数,其不但长得像,功能也是差不多的,只不过是做了扩展而已。
- plot3和fplot3
关于plot3函数,其基本用法如下:
one
plot3(x,y,z,参数)
twoplot(x1,y1,z1,x2,y2,z2,...,xn,yn,zn)
是不是似曾相识,没错,它和plot功能确实非常像,只是多了一维数据而已。如要画出sin(x)的三维图,只需这样就好:
x = [0:0.01:10]
y = x
z = sin(x)
plot3(x,y,z,'-r')
怎么样,是不是非常简单,假如要绘制个空间的螺旋线,其参数方程为:x=sint+tcost,y=cost-tsint,z=t,只需这样就好:
t = [0:0.1:10*pi]
x = sin(t)+t.*cos(t)
y = cos(t)-t.*sin(t)
z = t
plot3(x,y,z)
对于plot3函数来讲,它的参数x,y,z不止可以是一维数组,实际上:
- 参数x、y、z是同型矩阵时,以x、y、z对应列元素绘制曲线,曲线条数等于矩阵列数。
- 参数x、y、z中有向量,也有矩阵时,向量的长度与矩阵相符。
对于其不止一组数据的方法2,其作用与plot类似,每一组x、y、z向量构成一组数据点的坐标,绘制一条曲线。
而plot3函数的后面线型、颜色和数据点标记的参数则与plot完全一致。
对于fplot3函数,其基本引用方法如下:
fplot3(funx,funy,funz,tlims)
其中,funx、funy、funz代表定义曲线x、y、z坐标的函数,通常采用函数句柄的形式。tlims为参数函数自变量的取值范围,用二元向量[tmin,tmax]描述,默认为[-5,5],与fplot是几乎完全一致的,不再举例。
三维曲面
在做三维曲面图的时候,第一步往往是生成一个平面网格,这个平面网格是什么东西呢,其实就是用矩阵X、Y分别存储每一个小矩形顶点的x坐标与y坐标,矩阵X、Y就是该矩形区域的xy平面网格坐标矩阵:
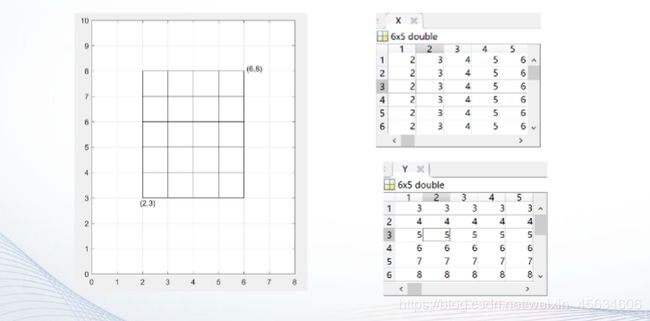
说的简单些,就是给我们要用的空间坐标系做个底面出来,本来x、y都是一维向量,它们也就是只能当两根轴,这个时候用新的两个X、Y矩阵来把空间坐标系的二维地面给表示出来,这样的话每一个[X,Y]就都能对应一个Z了,就是这个意思。在MATLAB中,产生平面区域内网格坐标矩阵有两种方法:
- 1.利用矩阵运算生成:
X = ones(size(y))*x
Y = y*ones(size(x))
- 2.利用meshgrid函数生成:
[X,Y] = meshgrid(x,y)
- 绘制三维曲面的函数
mesh(x,y,z,c)
surf(x,y,z,c)
mesh(z,c)
surf(z,c)
其中,x、y是网格坐标矩阵,z是网格点上的高度矩阵,c用于指定在不同高度下的曲面颜色。c省略时,颜色的设定正比于图形的高度。
当x、y省略时,z矩阵的第2维下标当作x轴坐标,z矩阵的第一维下标当作y轴坐标。
另外还有一些其它的绘制三维曲面的函数:
带等高线的三维网格曲面函数meshc
带底座的三维网格曲面函数meshz
具有等高线的曲面函数surfc
具有光照效果的曲面函数surfl
这些函数使用都和mesh还有surf大致相同,可自行练习了解。
//用4种方式绘制函数z=(x-1)^2+(y-2)^2-1的曲面图
//其中,x=[0,2],y=[1,3]
[x,y]=meshgrid(0:0.1:2,1:0.1:3)
z=(x-1).^2+(y-2).^2-1
subplot(2,2,1);meshc(x,y,z)
subplot(2,2,2);meshz(x,y,z)
subplot(2,2,3);surfc(x,y,z)
subplot(2,2,4);surfl(x,y,z)
- 标准三维曲面
[x,y,z]=sphere(n)
产生3个(n+1)阶的方阵,采用这3个矩阵可以绘制出圆心位于原点、半径为1的单位球体。
[x,y,z]=cylinder(R,n)
其中,参数R是一个向量,存放柱面各个等间隔高度上的半径,n表示在圆柱圆周上有n个间隔点,默认有20个间隔点。
peaks函数
调用格式:
peaks(n) >> p1=peaks(10)
peaks >> p2=peaks
peaks(V) >> p3=peaks(-3:0.2:3)
peaks(x,y) >> [x,y]=meshgrid(-2:0.1:2,0:0.1:5)
p4=peaks(x,y)
- fmesh函数和fsurf函数
用于绘制参数方程定义的曲面
fsurf(funx,funy,funz,uvlims)
fmesh(funx,funy,funz,uvlims)
其中,funx、funy、funz代表定义曲面x、y、z坐标的函数,通常采用函数句柄的形式。uvlims为funx、funy和funz的自变量的取值范围,用4元向量[umin,umax,vmin,vmax]描述,默认为[-5,5,-5,5]。
图形修饰辅助操作
到这里,不管是二维曲线三维曲线还是曲面,大家掌握的方法都差不多了,图大概率是能被我们做出来了哈哈哈,不过能把图做出来固然重要,可更重要的是还能做出美图来,这就离不开我们的图形修饰了,比如给做好的图形加个标题加个注释什么的,我们要做出来图,还要做出来细图,更要做出来美图,接下来文章将列举我们经常使用的并且很有用的图形修饰辅助操作。
基础绘图指令
除去上文所述plot等绘图函数命令之外,还有有一些其它修饰图形的常用命令。
| 指令 | 作用 |
|---|---|
| figure(num) | 新打开一个图形窗口,num为窗口序号 |
| hold on | 从指令开始,将后续所有图形绘制在一个figure窗口中 |
| hold off | 和hold on搭配使用,此指令开始,后续图形不再与之前图形绘制在一个窗口中 |
| axis on | 显示坐标轴 |
| axis off | 不显示坐标轴 |
| axis square | 使坐标轴区域为正方形 |
| axis normal | 自动调整轴的长宽比和数据单元的相对比例 |
| axis equal | 设置纵横比,使数据单元为各方面都一样 |
| axis equal tight | 将轴限制设置为数据的范围 |
| axis ij | 把坐标系统的原点放在左上角 |
| axis xy | 把原点放在左下角 |
这些呢是一些常用的辅助绘图指令,没有参数,直接在脚本输入就行,功能已经列在表中非常明确,大家可以自行练习查看实用效果。
接下来是一些带参数的绘图指令,它们可以帮你进行图形标注、坐标控制等等一系列功能,非常实用,记得好好学习。
图形标注函数
title(图形标题)
xlabel(x轴说明)
ylabel(y轴说明)
text(x,y,文本说明)
legend(图1,图2,...,参数...)
值得一提的是,上面这些函数的使用方法远不及示例这么简单,它们都有非常多的参数可供选择使用,示例只是列出最简单、最常用的方法,下面是两段代码:
//没有图形标注
x = 0:0.5:4*pi
y1 = sin(x)
y2 = cos(x)
y3 = 1./(1+exp(-x))
y4 = (1/(2*pi)^0.5).*exp(((-1).*(x-2*pi).^2)./(2*2^2))
plot(x,y1,x,y2,x,y3,x,y4)
//加上简单图形标注
title('四条函数图像')
xlabel('横坐标')
ylabel('纵坐标')
text(0,0,'猜猜我在哪')
legend('y1','y2','y3','y4','Location','southwest')
- 图形窗口分割函数subplot
subplot(m,n,p)
其中,m和n指定将窗口分成mXn个绘图区,p指定的是当前图像所在区域,如m=2,n=3,则一个figure窗口被分成2行三列供6个绘图区,可以容纳6个图形。若p=3,说明当前图像要被画进第三个窗口,也就是第二行第一列的窗口内。p小于等于mXn,如:
x = [0:0.1:10]
y1 = sin(x)
y2 = cos(x)
subplot(1,2,1)
plot(x,y1)
subplot(1,2,2)
plot(x,y2)
图形修饰处理
前面写了一些基本绘图指令,可以对我们的图形进行简单的修整,让其变得更完备更好看,接下来是一些对图形修饰的方法。
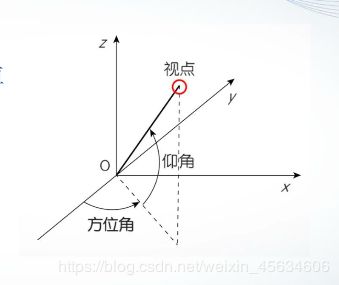
视点处理
- 方位角:视点与原点连线在xy平面上的投影与y轴负方向形成的角度,正值表示逆时针,负值表示顺时针。
- 仰角:视点与原点连线与xy平面的夹角,正值表示视点在xy平面上方,负值表示视点在xy平面下方。
- view函数
view(az,el)
其中az为方位角,el为仰角。系统默认的视点定义为方位角-37.5°,仰角30°。
//绘制函数z=(x-1)^2+(y-2)^2-1的曲面图,并从不同视点展示曲面
[x,y] = meshgrid(0:0.1:2,1:0.1:3)
z =(x-1).^2+(y-2).^2-1
subplot(2,2,1); mesh(x,y,z)
subplot(2,2,2); mesh(x,y,z);view(0,90)
subplot(2,2,3); mesh(x,y,z);view(90,0)
subplot(2,2,4); mesh(x,y,z);view(-45,-60)
色彩处理
默认的,向量元素在[0,1]范围内取值,3个元素一次表示红、绿、蓝三种颜色的相对亮度,称为RGB三元组即[R G B],如[0 0 1]是蓝色,[1 0 0]是红色,[1 1 1]是白色,[0 0 0]是黑色。(当然,也有在[0,255]内取值的,不再介绍)
- 色图(Colormap)
首先,创建一个色图矩阵方法如下:
cmap = colormap(parula(5))
其中,parula是内建色图中包含的一个种类,其中参数5可以是任何一个数值,它关系着色图矩阵的范围,一般来说使用的时候省略就好。内建色图如下:

- 指定当前图形使用的色图
//以peaks为例,先渲染图形,后紧跟色图种类即可
surf(peaks)
colormap hot
我们也可以不使用系统的色图矩阵,可以自定义任何色图矩阵。如创建一个灰色系列的色图矩阵:
c = [0,0.2,0.4,0.6,0.8,1.0]'
cmap = [c,c,c] //这样创建的矩阵和 cmap=gray(6)是一样的
surf(peaks)
colormap(cmap)
- 用shading函数来改变着色方式
参数如下:
| 名称 | 作用 |
|---|---|
| shading faceted | 每个网格片用其高度对应的颜色进行着色,默认网格线是黑色 |
| shading flat | 每个网格片用同一个颜色进行着色,网格线也用此颜色 |
| shading interp | 网格片内采用颜色插值处理 |
示例:使用同一色图,以不同着色方式绘制圆锥体
[x,y,z] =cylinder(pi:-pi/5:0,10)
colormap(lines)
subplot(1,3,1)
surf(x,y,z);
shading flat
subplot(1,3,2)
surf(x,y,z);
shading interp
subplot(1,3,3)
surf(x,y,z)
图形的裁剪处理
将图形中需要裁剪部分对应的函数值设置成NaN,这样在绘制图形时,函数值为NaN的部分将不显示出来,从而达到对图形进行裁剪的目的。
示例如下:
//绘制3/4圆
t = linspace(0,2*pi,100)
x = sin(t)
y = cos(t)
p = y>0.5
y(p) = NaN
plot(x,y)
axis([-1.1,1.1,-1.1,1.1])
axis square
grid on
其它
- 其实在Matlab中还有两个非常重要的函数:
set和get,它们两个能非常方便的创建、修改图形的各种属性,如改变坐标轴范围、设置字体和刻度点、设定线条风格等等,不过它们涉及到的使用更深入,在这里不再展开叙述,而事实上,对于我们非常熟知的figure,它也能加上参数来对窗格进行设置,这都是我们经常使用的,但也是经常忽略它们其它功能的函数,如果有兴趣,你可以继续的深入探索下去,更深入的学习能更方便的为我们所用。
总结
好了,感谢你能看到这里,对于这篇文章,它可能的侧重点不是完全教会我们怎么作图,而更多的也可能是提醒我们在Matlab里面可以进行如此操作,对于新手而言,很多没有系统的学习过Matlab的使用,可能里面的很多东西不是我们不会用,而是根本不知道,所以这篇文章大致列出来了很多非常常用的函数方法等,其中的示例仅仅是个示例,它们的用法还有很多,希望大家能够进行再次开拓,深入的了解每个方法的使用。最后,如果你觉得本篇文章对你有用,请点个赞,谢谢!