雷达线性调频信号的脉冲压缩处理

一、设计目的和意义

掌握雷达测距的工作原理，掌握匹配滤波器的工作原理及其白噪声背景下的匹配滤波的设计，线性调频信号是大时宽频宽积信号； 其突出特点是匹配滤波器对回波的多普勒频移不敏感以及更好的低截获概率特性。LFM 信号在脉冲压缩体制雷达中广泛应用；利用线性调频信号具有大带宽、长脉冲的特点，宽脉冲发射已提高发射的平均功率保证足够的作用距离；而接受时采用相应的脉冲压缩算法获得窄脉冲已提高距离分辨率， 较好的解决了雷达作用距离和距离分辨率之间的矛盾。而利用脉冲压缩技术除了可以改善雷达系统的分辨力和检测能力，还增强了抗干扰能力、灵活性，能满足雷达多功能、多模式的需要。

二、设计原理

1、 匹配滤波器

匹配滤波器（match filter）是最佳线性滤波器的一种，该滤波器的准则是输出信噪比最大，常用于通信、雷达等系统的接收机中，下面对其冲激响应/系统函数进行推导。
设该滤波器传递函数为H(f)H(f)，冲激响应为h(t)h(t)，输入信号为
r(t)=s(t)+n(t)

其中s(t)为输入信号，n(t)为高斯白噪声。设输入信号的频谱密度函数为S(f)，而高斯白噪声的单边功率谱为n0/2，其中n0为高斯白噪声单边功率谱密度。 该信号通过匹配滤波器输出如图1.1所示

其中：
S(t)=Acos(2πf_0 t+πμt^2) (0≤t≤τ)
h(t)=ks_t^ (t_0-t)
H(f)=kS_t^ (f)e^(-j2πft_0 )
τ^’=1/B=1/μτ**

在通信系统中，滤波器是其中重要部件之一，滤波器特性的选择直接影响数字信号的恢复。在数字信号接收中，滤波器的作用有两个方面，使滤波器输出有用信号成分尽可能强；抑制信号外带噪声，使滤波器输出噪声成分尽可能小，减少噪声对信号判决的影响。对最佳线形滤波器的设计有两种准则其中一种是是滤波器输出信噪比在某一特定时刻达到最大，由此而导出的最佳线性滤波器成为匹配滤波器。在数字通信中，匹配滤波器具有广泛的应用。因此匹配滤波器是指滤波器的性能与信号的特性取得某种一致，使滤波器输出端的信号瞬时功率与噪声平均功率的比值最大。

在信号处理中，匹配滤波器可以用来解调基频带脉冲信号，基频带脉冲信号意指信号内容为同一波形信号乘上一个常数，在每个周期出现，每个周期中代表着或多或少的信息量。匹配滤波器解调出来的结果其SNR
(Signal Noise Ratio)为最大的，匹配滤波器需要事先知道：1.传送的信号；2.信号的同步。这样才能解调出传送的信号。

此外，匹配滤波器也可用于模式识别、相似度测试（similarity measure）。

2、线性调频信号

线性调频信号指持续期间频率连续线性变化的信号，是一种常用的雷达信号。可以采用如下数学表达式表示：

S(t)=Acos(2πf_0 t+πμt^2) (0≤t≤τ)

其中：f0为中心频率；k=B/为调频频率；B为频率变化范围；tao为脉冲宽度；a(t)为线性调频脉冲的包络。

线性调频信号通过对载波频率进行调制以增加信号的发射带宽并在接收时实现脉冲压缩。由于线性调频信号具有较高的距离分辨力，当在速度上无法区分多目标时，可以通过增加目标距离测试解决多目标的分辨问题；同时在抗干扰方面，线性调频信号可以在距离上区分干扰和目标，因而可以有效地对抗拖曳式干扰，这使得线性调频信号在雷达波形设计中得到了广泛的应用。由于线性调频信号是通过一个发射脉冲实现距离高分辨的，因此该信号对目标多普勒频移不敏感，即使回波信号有较大的多普勒频移，脉冲压缩系统仍能起到压缩的作用。这将大大简化信号处理系统。

线性调频信号经过压缩处理接收后的信号幅度峰值是原来发射信号峰值的D的1/2次方（D为脉压比，等于脉冲宽度与B的乘积）倍，即输出脉冲峰值功率比输入脉冲峰值功率增大了D倍。在要求发射机输出功率一定的情况下，接收机输出的目标回波信号经过匹配滤波压缩处理，具有窄的脉冲宽度和更高的峰值功率，前者提高距离分辨率而后者符合探测距离远的要求，这便充分体现了脉压体制独特的优越性。从反侦察的角度来说，脉压雷达比普通雷达具有更强的生存能力。由于线性调频信号的幅度和信噪比更小，由侦察方程可知，同等灵敏度的侦察机其侦察距离为原来的D的负1/2次方，所以在雷达应用领域，脉压雷达具有功率优势，应用前景十分广阔。

3、LFM 信号的脉冲压缩

脉冲压缩技术是匹配滤波理论和相关接收理论的一个很好的实际应用。它的提出很好的解决了这样的一个问题：在发射端发射大时宽、带宽信号，以提高信号的速度测量精度和速度分辨力，而在接收端，将宽脉冲信号压缩为窄脉冲，以提高雷达对目标的距离分辨精度和距离分辨力。

三、MATLAB具体仿真

匹配滤波在通信和雷达等系统中有很多应用，其中以雷达系统中的脉冲压缩较为典型，本文以雷达系统中的脉冲压缩(pulse compress)为例，进行仿真。

在雷达目标检测中，希望距离分辨率和探测威力都足够大。而距离分辨率与发射波形的时宽成反比，探测威力（能量）与发射波形的时宽成正比。若发射波形为方波，其时宽τ与带宽B乘积约等于1，说明距离分辨率和探测威力是相互矛盾的。此时采用线性调频信号，可以很好的解决这个矛盾。
对于一个理想的脉冲压缩系统， 要求发射信号具有非线性的相位谱， 并使其包络接近矩形；其中 S(t )就是信号 s(t)的复包络。由傅立叶变换性质， S(t)与 s(t)具有相同的幅频特性，只是中心频率不同而已。因此， Matlab 仿真时，只需考虑S(t)。

下面对脉冲压缩进行仿真，仿真参数设置如下

参数	取值
信号带宽	40MHz
信号时宽	20μs
脉冲周期	2ms
采样频率	20MHz
信噪比	20dB
目标距离	T∗fs/2

以下Matlab 程序产生的线性调频信号，并作出其时域波形和幅频特性，如图：

对应代码：

%%demo of chirp signal
T=20e-6;
B=40e6;%chirp frequency modulation bandwidth 30MHz
K=B/T; %chirp slope
Fs=2*B;Ts=1/Fs; %sampling frequency and sample spacing
N=T/Ts;
t=linspace(-T/2,T/2,N);
St=exp(j*pi*K*t.^2); %generate chirp signal
subplot(211)
plot(t*1e6,St);
xlabel('Time in u sec');
title(' 线性调频信号');
grid on;axis tight;
subplot(212)
freq=linspace(-Fs/2,Fs/2,N);
plot(freq*1e-6,fftshift(abs(fft(St))));
xlabel('Frequency in MHz');
title(' 线性调频信号的幅频特性');
grid on;axis tight;

以下Matlab 程序段仿真了LFM信号的脉冲压缩，仿真结果如图:

图中，时间轴进行了归一化，（t /(1/ B)= t *B）。图中反映出理论与仿真结果吻合良好。
对应代码：

%%demo of chirp signal after matched filter
T=20e-6;
B=40e6; %chirp frequency modulation bandwidth 30MHz
K=B/T; %chirp slope
Fs=10*B;Ts=1/Fs; %sampling frequency and sample spacing
N=T/Ts;
t=linspace(-T/2,T/2,N);
St=exp(j*pi*K*t.^2); %chirp signal
Ht=exp(-j*pi*K*t.^2); %matched filter
Sot=conv(St,Ht); %chirp signal after matched filter
subplot(211)
L=2*N-1;
t1=linspace(-T,T,L);
Z=abs(Sot);Z=Z/max(Z); %normalize
Z=20*log10(Z+1e-6);
Z1=abs(sinc(B.*t1)); %sinc function
Z1=20*log10(Z1+1e-6);
t1=t1*B;
plot(t1,Z,t1,Z1,'r.');
axis([-15,15,-50,inf]);grid on;
legend('emulational','sinc');
xlabel('Time in sec \times\itB');
ylabel('幅度,dB');
title(' 傅里叶变换后的线性调频信号');
subplot(212) %zoom
N0=3*Fs/B;
t2=-N0*Ts:Ts:N0*Ts;
t2=B*t2;
plot(t2,Z(N-N0:N+N0),t2,Z1(N-N0:N+N0),'r.');
axis([-inf,inf,-50,inf]);grid on;
set(gca,'Ytick',[-13.4,-4,0],'Xtick',[-3,-2,-1,-0.5,0,0.5,1,2,3]);
xlabel('Time in sec \times\itB');
ylabel('幅度,dB');
title(' 傅里叶变换后的线性调频信号(Zoom)');

以下Matlab 程序段仿真了线性调制信号和噪声的生成，仿真结果如图:

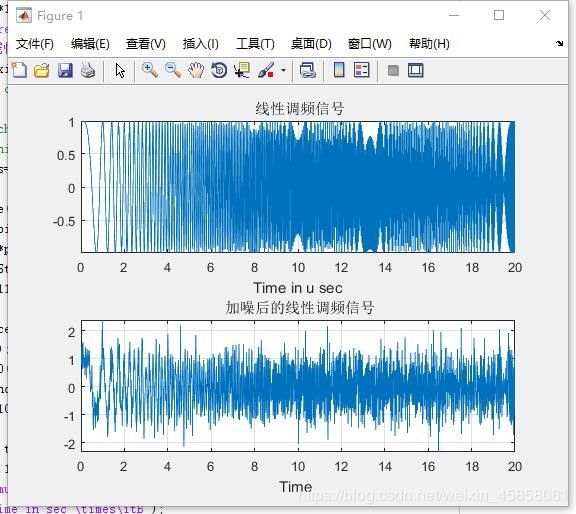
对应代码：

% 加白噪声后的线性调频信号
T=20e-6;
B=40e6; %chirp frequency modulation bandwidth 30MHz
K=B/T; %chirp slope
Fs=2*B;Ts=1/Fs; %sampling frequency and sample spacing
N=T/Ts;
t=linspace(0,T,N);
St=exp(j*pi*K*t.^2);
subplot(211)
plot(t*1e6,St);
xlabel('Time in u sec');
title(' 线性调频信号');
grid on;axis tight;
SNR=20；
x=awgn(St, 5); %generate chirp signal
subplot(212)
plot(t*1e6,x);
xlabel('Time ');
title(' 加噪后的线性调频信号');
grid on;axis tight;

实际实际雷达系统中， LFM 脉冲的处理过程如图：

雷达回波信号 sr (t )经过正交解调后， 得到基带信号，再经过匹配滤波脉冲压缩后就可以作出判决。正交解调原理如图：

雷达回波信号经正交解调后得两路相互正交的信号I(t) 和Q(t)。一种数字方法处理的的匹配滤波原理如图：

以下为经过脉冲压缩输出的已加噪声的线性调频信号（模拟雷达回波信号）的matlab仿真结果，仿真结果如图:

四、小结

本文首先介绍了匹配滤波器的工作原理，特性特点；其次介绍了LFM 信号的形式以及matlab 的仿真情况，然后从雷达信号处理上进行改进，最后在对LFM 信号进行matlab 仿真，对LFM 在加噪前后脉冲压缩匹配滤波的仿真情况进行详细的分析，明确了脉冲压缩技术不但降低了对雷达发射机峰值功率的要求， 也解决雷达作用距离和距离分辨力之间的矛盾； 在对低截获概率雷达信号处理中将有广阔的应用前景。

参考文献

【1】信号与系统（第二版） 西安交通大学出版社
【2】matlab 基础与编程入门（第二版）西安电子科技大学出版社
【3】随机信号分析（第一版） 科学出版社
【4】雷达原理（第三版）西安电子科技大学出版社