基于翻译模型（Trans系列）的知识表示学习

翻译模型（Trans）

解决问题：知识表示与推理

将实体向量表示（Embedding）在低维稠密向量空间中，然后进行计算和推理。

主要应用：triplet classification, link prediction

---

目前基于翻译模型（Trans系列）的知识表示学习的研究情况

• TransE, NIPS2013, Translating embeddings for modeling multi-relational data
• TransH, AAAI2014, Knowledge graph embedding by translating on hyperplanes
• TransR, AAAI2015, Learning Entity and Relation Embeddings for Knowledge Graph Completion
• TransD, ACL2015, Knowledge graph embedding via dynamic mapping matrix
• TransA, arXiv2015, An adaptive approach for knowledge graph embedding
• TranSparse, AAAI2016, Knowledge graph completion with adaptive sparse transfer matrix
• TransG, arXiv2015, A Generative Mixture Model for Knowledge Graph Embedding
• KG2E, CIKM2015, Learning to represent knowledge graphs with gaussian embedding

---

TransE: 多元关系数据嵌入（Translation embeddings for modeling multi-relation data）

问题：如何建立简单且易拓展的模型把知识库中的实体和关系映射到低维向量空间中，从而计算出隐含的关系？
方案：将实体与关系嵌入到同一低维向量空间。

这篇文章提出了一种将实体与关系嵌入到低维向量空间中的简单模型，弥补了传统方法训练复杂、不易拓展的缺点，对实体和关系的建模十分简单明了，可解释性也很强。尽管现在还不清楚是否所有的关系种类都可以被这种方法建模，但目前这种方法相对于其他方法表现不错。在后续的研究中，TransE更是作为知识库vector化的基础，衍生出来了很多变体。

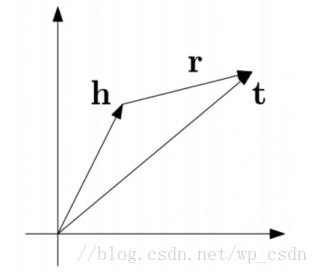
受word2vec启发，利用了词向量的平移不变现象。将每个三元组实例 (head，relation，tail) 中的关系 relation 看做从实体 head 到实体 tail 的翻译，通过不断调整h、r和t (head、relation 和 tail 的向量)，使 (h + r) 尽可能与 t 相等，即 h + r ≈ t。数学上表示就是通过约束 d(h+l,t)=||(h+r)−t||22≈0 d ( h + l , t ) = | | ( h + r ) − t | | 2 2 ≈ 0 来对实体和关系建模，将它们映射到相同的向量空间中。
其损失函数表示如下：

L=∑(h,l,t)∈S∑(h′,l′,t′)∈S′(h,l,t)[γ+d(h+l,t)−d(h′+l′,t′)]+ L = ∑ ( h , l , t ) ∈ S ∑ ( h ′ , l ′ , t ′ ) ∈ S ( h , l , t ) ′ [ γ + d ( h + l , t ) − d ( h ′ + l ′ , t ′ ) ] +

其中， [x]+ [ x ] + 表示 x x 的正数部分， γ γ 表示margin， S′h,l,t={(h′,l,t|h′∈E)}∪{(h,l,t′|t′∈E)} S h , l , t ′ = { ( h ′ , l , t | h ′ ∈ E ) } ∪ { ( h , l , t ′ | t ′ ∈ E ) }

---

TransH: 将知识嵌入到超平面（Knowledge graph embedding by translating on hyperplanes）

问题：对知识库中的实体关系建模,特别是一对多,多对一,多对多的关系。设计更好的建立负类的办法用于训练。
方案：将实体和关系嵌入到同一的向量空间，但实体在不同关系中有不同的表示。

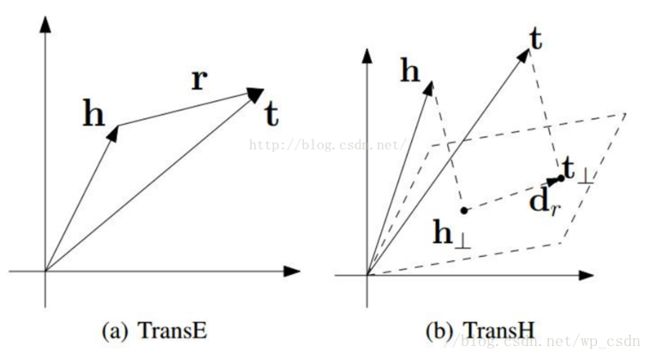
在数学表示上面就可以很简单的看出TransH与TransE的区别：TransE中三元组 (h,r,t) ( h , r , t ) 需要满足 d(h+r,t)=||(h+r)−t||22≈0 d ( h + r , t ) = | | ( h + r ) − t | | 2 2 ≈ 0 ，而TransH中三元组 (h,r,t) ( h , r , t ) 则需要满足 d(h+r,t)=||(h−wTrhwr)+dr−(t−wTrtwr)||22≈0 d ( h + r , t ) = | | ( h − w r T h w r ) + d r − ( t − w r T t w r ) | | 2 2 ≈ 0 ，其中 wr,dr∈Rk w r , d r ∈ R k 表示关系。

---

TransR: 实体和关系分开嵌入（Learning Entity and Relation Embeddings for Knowledge Graph Completion）

问题：一个实体是多种属性的综合体，不同关系关注实体的不同属性。直觉上一些相似的实体在实体空间中应该彼此靠近，但是同样地，在一些特定的不同的方面在对应的关系空间中应该彼此远离。
方案：将实体和关系嵌入到不同的空间中，在对应的关系空间中实现翻译。

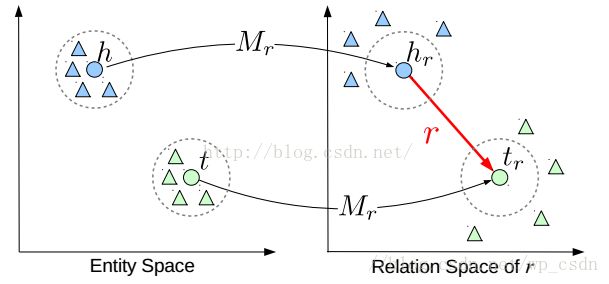
TransR在TranE的基础上的改进，在数学上的描述看起来会更加直观：对于每一类关系，不光有一个向量 r r 来描述它自身，还有一个映射矩阵 Mr M r 来描述这个关系所处的关系空间，即对于一个三元组 (h,r,t) ( h , r , t ) ，需要满足 d(h,r,t)=||hr+r−tr||22=||hMr+r−tMr||22≈0 d ( h , r , t ) = | | h r + r − t r | | 2 2 = | | h M r + r − t M r | | 2 2 ≈ 0 。

---

TransD: 通过动态映射矩阵嵌入（Knowledge graph embedding via dynamic mapping matrix）

问题：TransR过于复杂，在TransR的基础上减少参数。。。
方案：实体和关系映射到不同的空间中，用两个向量表示实体或关系，一个 (h,r,t) ( h , r , t ) 表征实体或关系，另一个 (hp,rp,tp) ( h p , r p , t p ) 用来构造动态映射矩阵。

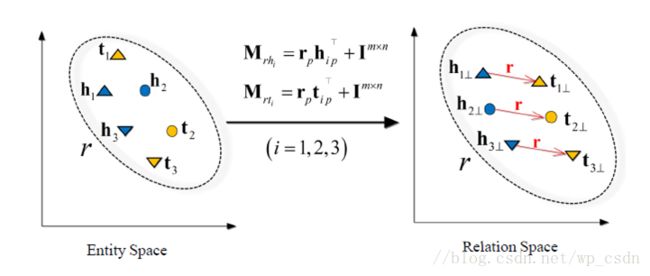
TransD在TransR的基础上，将关系的映射矩阵简化为两个向量的积，图中 Mrh=rphp+Im∗n M r h = r p h p + I m ∗ n 与 Mrt=rptp+Im∗n M r t = r p t p + I m ∗ n 表示实体 h h 与实体 r r 映射到关系空间的矩阵，那么对于三元组 (h,r,t) ( h , r , t ) ，需要满足 d(h,r,t)=||Mrhh+r−Mrtt||22≈0 d ( h , r , t ) = | | M r h h + r − M r t t | | 2 2 ≈ 0 。

---

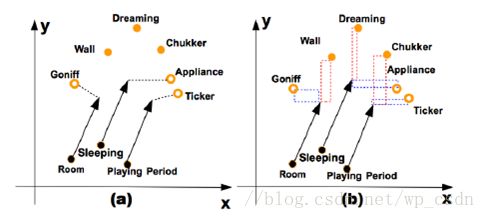
TransA: 自适应的度量函数（An adaptive approach for knowledge graph embedding）

问题：如何解决了translation-based 知识表示方法存在的过于简化损失度量，没有足够能力去度量/表示知识库中实体/关系的多样性和复杂性的问题。
方案：更换度量函数，区别对待向量表示中的各个维度，增加模型表示能力。

光看这张图可能会意义不明，其实模型在TransE的基础上的改进也非常小，简单地说就是给实体/关系的每一个维度都加上了一个权重，增加模型的表示能力。
TransE模型的一般形式为： d(h+l,t)=||(h+r)−t||22 =(h+r−t)T(h+r−t) d ( h + l , t ) = | | ( h + r ) − t | | 2 2   = ( h + r − t ) T ( h + r − t )
TransA对于每一类关系，给实体/向量空间加上了一个权重矩阵 Wr W r ，然后可以对权重向量做矩阵分解 Wr=LTrDrLr W r = L r T D r L r ，最后TransA的数学形式为： d(h+l,t)=(h+r−t)TWr(h+r−t)=(Lr|h+r−t|)TDr(Lr|h+r−t|)) d ( h + l , t ) = ( h + r − t ) T W r ( h + r − t ) = ( L r | h + r − t | ) T D r ( L r | h + r − t | ) ) 。

---

TranSpare: 自适应稀疏转换矩阵（Knowledge graph completion with adaptive sparse transfer matrix）

问题： heterogeneous（异质性：有的实体关系十分复杂，连接许多不同的实体，而有些关系又非常简单）和unbalanced（不均衡性：很多关系连接的head和tail数目很不对等）。
关键：针对不同难度的实体间关系，使用不同稀疏程度的矩阵（不同数量的参数）来进行表征，从而防止对复杂关系欠拟合或者对简单关系过拟合；对头尾两种实体采用不同的投影矩阵，解决头尾实体数目不对等的问题。

针对异质性（heterogeneous）

在TransR的基础上，使用可变的稀疏矩阵代替TransR的稠密矩阵：关系连接的实体数量越多，关系越复杂，矩阵约稠密；关系链接的实体数量越少，关系越简单，矩阵约稀疏。
使用参数 θr θ r 描述关系 r r 的复杂程度，使用一个稀疏矩阵 Mr(θr) M r ( θ r ) 和一个关系向量 r r 表示一类关系，其中 θr=1−(1−θmin)Nr/Nr∗ θ r = 1 − ( 1 − θ m i n ) N r / N r ∗ ， r∗ r ∗ 表示连接实体数量最多的关系， Nr∗ N r ∗ 为其连接的实体的数量， θmin θ m i n 为设置的超参，表示关系 r∗ r ∗ 的稀疏程度。
以此为基础，对于一个关系三元组 (h,r,t) ( h , r , t ) ，需要满足的约束为 d(h,r,t)=||hp+r−tp||22=||Mr(θr)h+r−Mr(θr)t||22≈0 d ( h , r , t ) = | | h p + r − t p | | 2 2 = | | M r ( θ r ) h + r − M r ( θ r ) t | | 2 2 ≈ 0 。

针对不平衡性（unbalanced）

与上述方法类似，不同点在于对于每个关系三元组 (h,r,t) ( h , r , t ) ，头尾实体的映射矩阵为两个不同的稀疏矩阵，其稀疏程度与该关系的头尾实体的数目有关，即头/尾涉及到的实体越多，矩阵约稠密；反之涉及到的实体越少，矩阵越稀疏。
使用参数 θhr θ r h 与 θtr θ r t 分别描述头尾实体映射矩阵的稠密程度，则 θlr=1−(1−θmin)Nlr/Nl∗r∗ θ r l = 1 − ( 1 − θ m i n ) N r l / N r ∗ l ∗ ，其中 Nlr N r l 表示关系 r r 在位置 l l （即头或者尾）上关联的实体数量， Nl∗r∗ N r ∗ l ∗ 则表示关系 r∗ r ∗ 在位置 l∗ l ∗ （即头或者尾）上关联的实体数量最多的关系的数量，对应的设置超参 θmin θ m i n 表示其稀疏程度。
对于一个关系三元组 (h,r,t) ( h , r , t ) ，TransSparse需要满足的约束为 d(h,r,t)=||hp+r−tp||22=||Mhr(θhr)h+r−Mtr(θtr)t||22≈0 d ( h , r , t ) = | | h p + r − t p | | 2 2 = | | M r h ( θ r h ) h + r − M r t ( θ r t ) t | | 2 2 ≈ 0 。

---

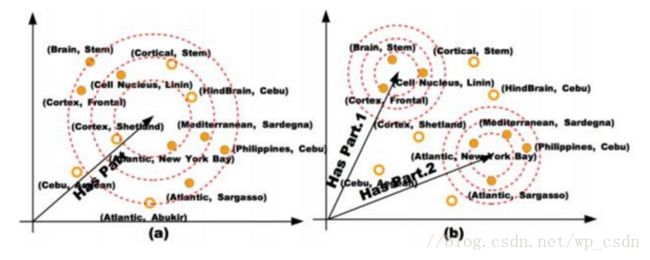
TransG: 高斯混合模型（A Generative Mixture Model for Knowledge Graph Embedding）

问题：解决多关系语义的问题，同一种关系在语义上是不同的，eg, (Atlantics, HasPart, NewYorkBay)与(Table, HasPart, Leg)。
方案：利用贝叶斯非参数高斯混合模型对一个关系生成多个翻译部分，根据三元组的特定语义得到当中的最佳部分。

考虑到一种关系存在的多语义问题，相当于对关系进行了细化，就是找到关系的隐形含义，最终从细化的结果中选出一个最佳的关系语义。

---

KG2E: 高斯分步表示实体和关系（Learning to represent knowledge graphs with gaussian embedding）

关键：使用Gaussian Distribution 来表示实体和关系，提出了用Gaussian Distribution的协方差来表示实体和关系的不确定度的新思想，提升了已有模型在link prediction和triplet classification问题上的准确率。

ps. 最后两种方法设计到使用高斯混合分步表示实体，后面有时间了再更新。