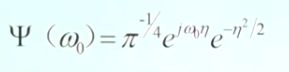【智能穿戴算法】--数字信号分析与处理基础知识
文章目录
- 一、信号的时域分析
- 1.1信号波形参数识别
- 1.2检测方法 过零检测法
- 1.3数字信号微分与数字信号积分
- 二、信号的频域分析
- 2.1周期信号的频谱分析
- 2.2 信号的频谱分析
- 2.3数字信号的频谱计算方法
- 三、信号的时差域相关分析
- 3.1信号的相关系数
- 3.2 相关应用
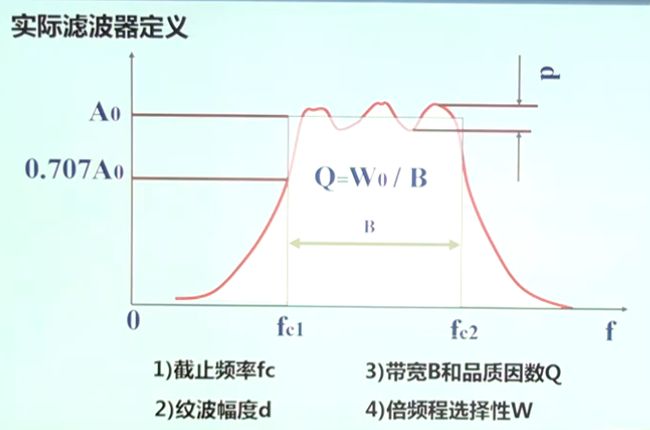
- 3.3 数字滤波器和模拟滤波器的区别
- 四、信号的幅值域分析
- 4.1概率密度曲线与概率分布曲线的应用
- 五、信号的数字滤波
- 5.1滤波器概念
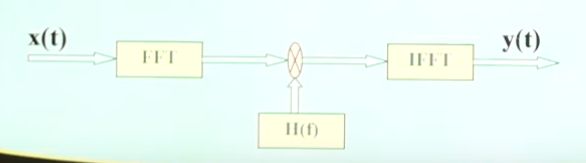
- 5.2频率域滤波:
- 5.3时域滤波
- 5.4 时域FIR滤波器
- 5.5 IIR滤波器
- 5.6 其他滤波器
- 5.7 数字音乐均衡器的设计
- 六、信号的时频分析简介
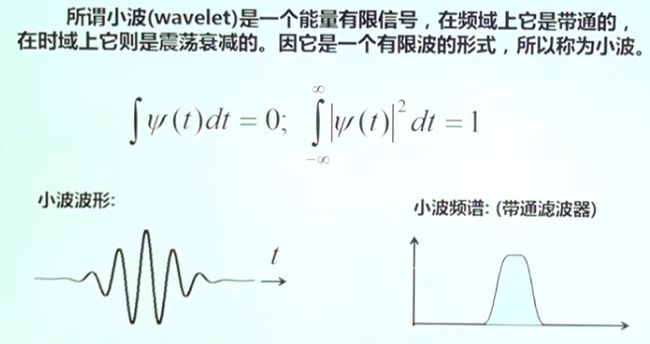
- 6.1 信号小波分析
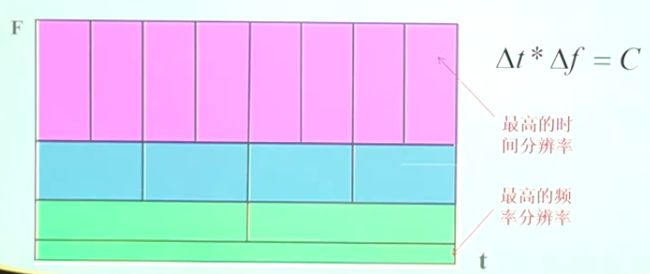
- 6.2四种分析方法时频分析精度对比
- 6.3连续小波
- 6.5离散小波变换
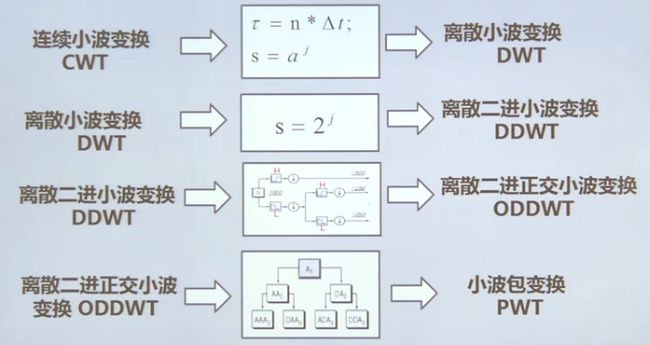
- 6.6几种小波变换的关系
一、信号的时域分析
采样定理:F>2Fs; F>5Fs
频率混迭:采样频率不满足采样定理时,信号中的高频成分会被不正确的采样成低频成分,这一现象称为频率混迭。
1.1信号波形参数识别
- 周期、频率
- 峰值、双峰值:max(singal)-min(singal)
- 初相位
- 均值:反映信号变化的中心趋势,称为直流分量:mean(singal)
- 均方值:表示信号强度,其平方根为有效值(RMS)
- 方差:反映信号绕均值的波动程度:std(singal)
1.2检测方法 过零检测法
过零点有最大的斜率
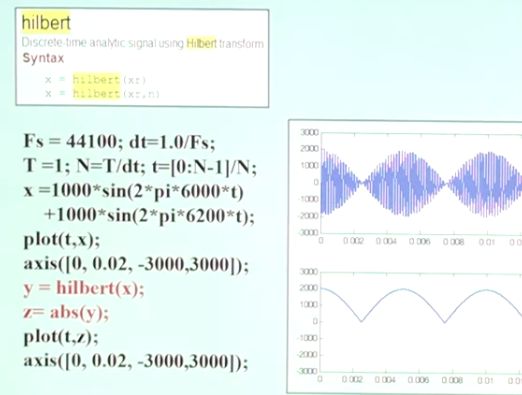
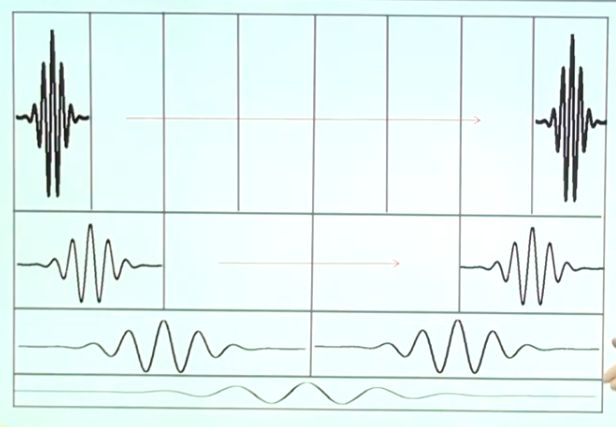
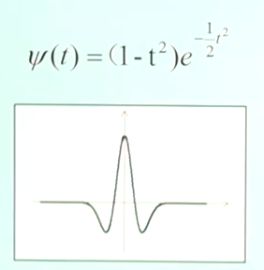
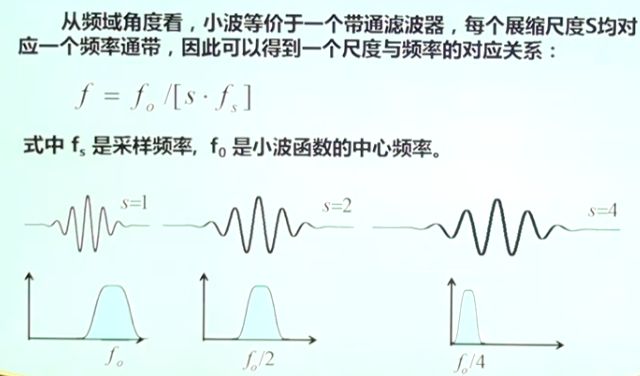
上升沿过零点条件:x(k)<=0 相邻两个过零点时间差就是周期,第一个过零点位置与周期比例是初相位。 峰值检测原理:目前峰值检测方法的核心是在某一个或某几个尺度内搜索小波变换模极大极小值之间的过零点,在此基础上对过零点位置相对于峰值位置的误差进行一定程序的修正。 过零检测MATLAB代码: 数字信号先微分再积分,可还原信号,但与原信号相比,丢失初始值信息。 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gFbyBQLL-1590892967028)(https://s1.ax1x.com/2020/04/09/G4gpGQ.png)] [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eW2Fx5dp-1590892967031)(https://s1.ax1x.com/2020/04/09/G4g92j.png)] 利用信号的峰值进行索道钢丝断裂检测 x(t)=x(t+nT);基频f0=1/T。该信号可以用傅里叶级数分解。 利用三角正交函数集对信号进行分解。 信号的傅里叶级数分解: 周期信号在三角函数集下的投影:x(t)=x(t+nT) => {cos(2×pi×i×f0×t),sin(2×pi×i×f0×t)} 周期信号频谱图的特点: 连续域上的积分求解映射到离散域上的求和操作。 MATLAB中使用yn=fft(x,n)函数,数据长度n必须是2的幂次方,结果yn是投影系数实部an和虚部bn组成。 fft注意事项: 1.信号截断:对信号进行截断,看做以W长度为大小的周期信号进行处理。由于信号截断的原因,产生了能量泄漏,即使信号频率与频谱离散取样点不相等,也能得到该频率分量的一个近似值。 2.能量泄漏: 信号截断函数:能量泄漏分主瓣泄漏和旁瓣泄漏,信号加窗截断是用窗函数与信号相乘,然后截断,减小周期延拓边界的跳变;抑制旁瓣能量泄漏。信号加窗减小栅栏效用。 平顶窗用的多 3.离散傅里叶变换 数字信号->信号截断->周期延拓->截断的周期信号 4.FFT [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-2RjyHiIk-1590892967051)(https://s1.ax1x.com/2020/04/14/GzAKCq.png)] 相关函数的性质: - 影响采样频率; - 影响有效A/D位数; 幅值域分析称为信号的概率密度曲线和概率分布曲线分析。 MATLAB相关函数: 滤波的条件:有用信号与噪声信号在频率域上(频带)不重叠。 当采样信号中有较高频率成分信号时,首先使用模拟滤波器进行低通滤波,再进行信号的预处理。这样可以降低信号的采样频率,减小运算量 。 在信号去噪处理中,判断去噪效果的好坏主 要有信噪比 (SNR) 和信号重构均方误差(MSE) 2 个标准。一般来说, SNR 越大, MSE 越小,则去 噪效果越好。 均方根误差的定义为: 时域数字滤波就是将信号与滤波器的单位脉冲响应(Z域滤波器系数)进行卷积;寻找所需的滤波器单位脉冲响应的过程称为滤波器设计,信号卷积过程称为滤波。 求取系数的过程就是数字滤波器的设计过程。 时域滤波的关键是设计出Z变换形式的滤波器,就可以快速写出滤波公式。 MATLAB函数:fir1函数()、fir2()函数、firls()函数 滤波后的数据出现头部暂态现象,滤波器的系数(阶数越高)越长,头部暂态现象越长。 设计方法: 设计方法:先借助模拟滤波器,再将模拟滤波器转为数字滤波器; 高通滤波器可以消除信号中的缓慢波动的低频现象。传感器晃动可能产生低频干扰。 低通滤波器可以消除信号中的细小快速(细小毛刺)波动的高频现象。 陷波滤波器(notch filter):属于带阻滤波器,其阻带很窄。可以快速衰减某一频率点信号,已达到阻止该频率信号的滤波效果。消除工频50Hz干扰 MATLAB中的使用:iirnotch(wo,bw) 尖峰滤波器(peak filter):属于带通滤波器,其通带很窄。可以只让某一频率点信号通过,阻止其他频率成分的过滤效果。 MATLAB中的使用:iirpeak(wo,bw) 半带滤波器:通带和阻带对称 希尔伯特全通滤波器90°相移滤波器:用于包络信号的检波处理。希尔伯特变换可以提取波形的包络 幅度调制与解调amplitude modulatiom: 高频信号的传输距离更远。 MATLAB中的使用: 方法 小波分析:可变长度窗口 dt*df=C 针对信号的不同频率特征,采用不同的窗口大小,如下图所示。低频信号使用宽窗口,高频信号使用窄窗口。 每个小波变换都有一个母小波,同时还有一个尺度函数,也被成为父小波。任何小波变换的小波基函数,其实就是对母小波和父小波缩放和平移后得到的集合。小波变换允许更加精确的局部描述以及信号特征的分离。一个傅立叶系数通常表示某个贯穿整个时间域的信号分量,因此,即使是临时的信号,其特征也被强扯到了整个时间周期去描述。而小波展开的系数则代表了对应分量它当下的自己,因此非常容易诠释。 窗口越宽,时间分辨率越低,频率分辨率越高; 连续小波变换的数学定义:信号与展缩小波函数的卷积分得到小波系数CWT。 通过展缩因子调节小波变换窗口的范围和频域轴的位置。 几种常见的小波函数 MATLAB中的小波函数:wavelet 小波变换结果与选择的小波函数有关 STFT谱阵和小波尺度谱阵的关系 谱阵STFT,等精度,代表信号代表在时–频面上的能量分别;Y轴为时间轴 小波尺度谱阵,变精度,尺度越小,精度越高;尺度越大,频率精度越低。代表在时–频面上的能量分别;X轴为时间轴 尺度与频率的关系 时移因子直接按信号的采样间隔进行离散化,尺度因子则按照指数规律离散化 离散小波分解–>信号的多尺度滤波模型 离散二进小波变换:s=s^j-1,s={1,2,4,8…}, 正交小波分解dwt:每一级正交小波分解后数据量不增加。 MATLAB函数:wavedec()分解 waverec()合成 小波包变换:wpdec()分解 wprec()合成 【参考】:B站:【公开课】数字信号分析理论与实践(基于matlab) - 华中科技大学1.3数字信号微分与数字信号积分
二、信号的频域分析
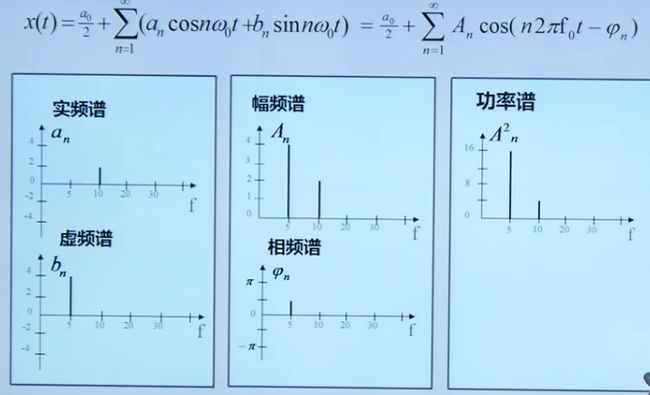
2.1周期信号的频谱分析
三角函数集{cos(2×pi×i×f0×t),sin(2×pi×i×f0×t),i=1,2,3,4,5} 中任意两个函数相乘,积分值为零。


2.2 信号的频谱分析
Yn=an+j*bn,n=1,2,3…Y0表示直流分量,Y1表示一次谐波f=f0时的值,Y2表示二次谐波f=2f0时的值.
2.3数字信号的频谱计算方法
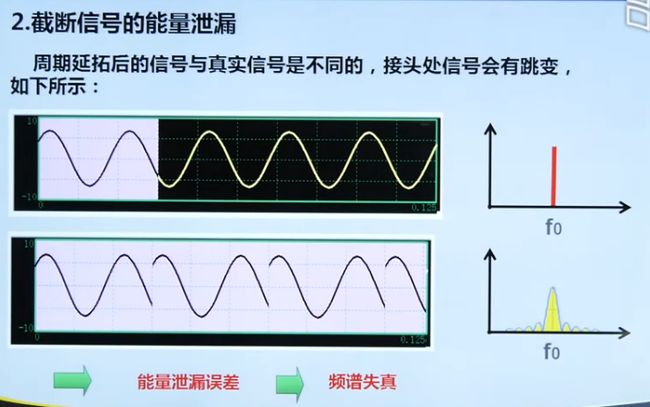
信号整周期截断。
加窗–>控制能量泄漏–>减小栅栏效应误差;

按照三角函数的展开式求出a0 an bn这三个傅里叶级数的系数三、信号的时差域相关分析
3.1信号的相关系数
工程上通常只关心分子部分。使用FFT计算自相关函数
% 自相关滤波
N=1024;
T=0.2;
x=linspace(0,T,N);
y=sin(2*pi*50*x);
figure;
plot(x,y);
s=xcorr(y,'unbiased'); %加修正的相关系数
x1=linspace(-T,T,2*N-1);
figure;
plot(x1,s);
3.2 相关应用
3.3 数字滤波器和模拟滤波器的区别
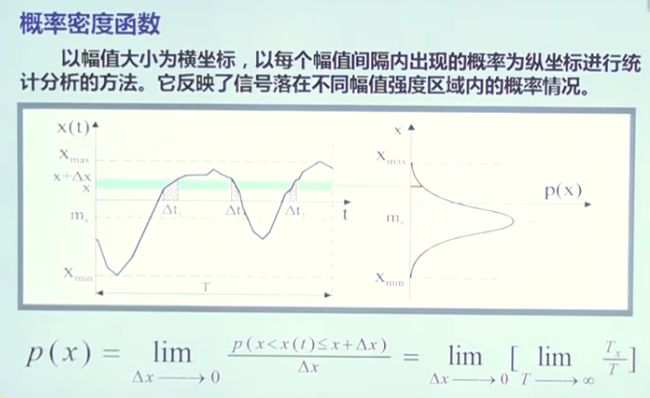
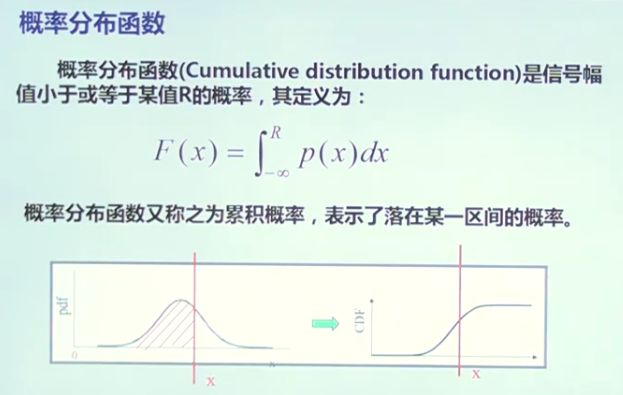
四、信号的幅值域分析
4.1概率密度曲线与概率分布曲线的应用
五、信号的数字滤波

5.1滤波器概念
5.2频率域滤波:

长数据信号的FFT频域滤波:对长信号进行帧划分,比如划成1024点,再进行FFT滤波;再采样帧数据重叠技术,对重迭部分进行掐头去尾处理,比如舍去64点。5.3时域滤波
5.4 时域FIR滤波器
使用数组定义滤波器
5.5 IIR滤波器
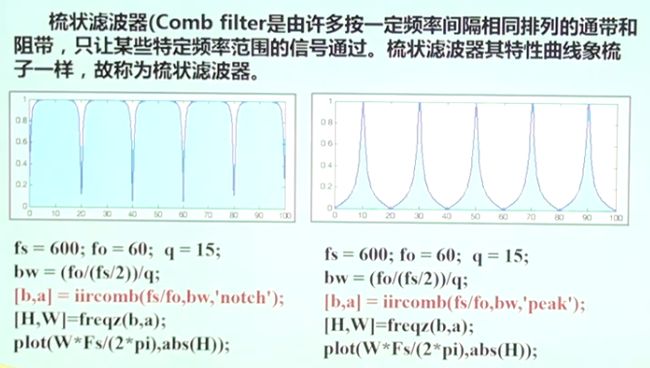
5.6 其他滤波器
[H,W]=freq(b,a):画出滤波器的频率特性
5.7 数字音乐均衡器的设计
六、信号的时频分析简介
6.1 信号小波分析
窗口越窄,时间分辨率越高,频率分辨率越低;
6.2四种分析方法时频分析精度对比
6.3连续小波

[C,L]=wavedec(x,3,'db3'); %多层一维小波分解
wpt=wpdec(x,3,'db1','shannon'); %小波包分解:
[cd1,cd2,cd3]=detcoef(C,L,[1,2,3]); %获取细节系数
ca3=appcoef(C,L,'db3',3); %获取近似系数
A=wrcoef('a',C,L,'db3',3); %对信号的低频部分重构,A表示信号的最小频率
D1=wrcoef('d',C,L,'db3',3); %对信号的高部分重构,D1表示信号的最大频率
D2=wrcoef('d',C,L,'db3',3); %对信号的高部分重构,D1表示信号的第二大频率
D3=wrcoef('d',C,L,'db3',3); %对信号的高部分重构,D1表示信号的第三大频率
横纵坐标轴的方向不一样6.5离散小波变换
增加数据量
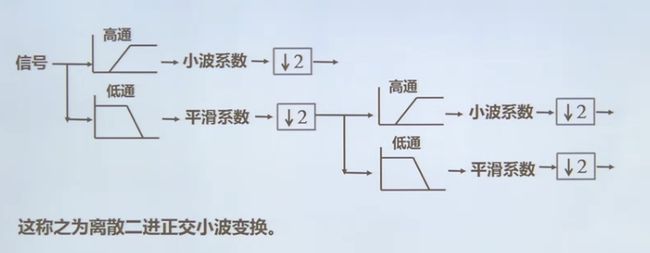
要求:滤波器对{hj,gj}是正交的。
滤波:将该频域下小波系数置为零。6.6几种小波变换的关系