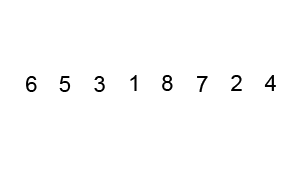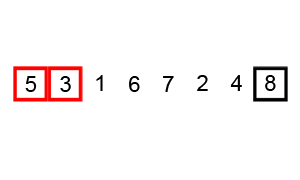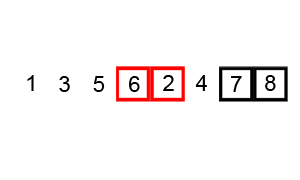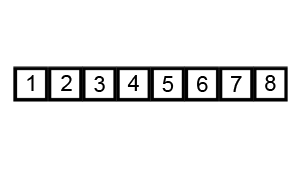面试中常见的排序算法
文章参考了:http://blog.csdn.net/u010850027/article/details/49362279
http://www.cnblogs.com/0201zcr/p/4763806.html
每次面试中都会考到排序算法,这里集中总结下。话不多说,先上张图:
这张图一般会基本包含了面试中常见的排序算法,内部排序是说数据在内存里排序,外部排序是处理在硬盘上的一些数据的排序(比如数据太多没法都读到内存里)。我们从上到下挨个分析,可以看到选择排序,插入排序,交换排序分别有三组,下面可以看作对上面简单排序的优化。
一、直接选择排序
这个简单,直接上图。
如上所示的一组序列为8、5、2、6、9、3、1、4、0、7,首先我们在这个里面选取一个最小的数当然最大的也可以,具体根据要求来进行选择,我们以从小到大的顺序进行排列,首先,我们选取一个最小的数字0,0和8进行交互位置,经过第一次选择之后,序列的顺序变成0、5、2、6、9、3、1、4、8、7,接着进行第二次选择,再选择一个最小的数字1,1和5交互位置,依次类推,直到该序列是有序序列为止。
java代码如下:
/**
* 选择排序算法
* 在未排序序列中找到最小元素,存放到排序序列的起始位置
* 再从剩余未排序元素中继续寻找最小元素,然后放到排序序列末尾。
* 以此类推,直到所有元素均排序完毕。
* @param numbers
*/
public static void selectSort(int[] numbers)
{
int size = numbers.length; //数组长度
int temp = 0 ; //中间变量
for(int i = 0 ; i < size ; i++)
{
int k = i; //待确定的位置
//选择出应该在第i个位置的数
for(int j = size -1 ; j > i ; j--)
{
if(numbers[j] < numbers[k])
{
k = j;
}
}
//交换两个数
temp = numbers[i];
numbers[i] = numbers[k];
numbers[k] = temp;
}
}二、堆排序
接着我们来看选择排序中的另一种排序—堆排序,由上面的直接选择排序分析,我们知道,在n个键值中选出最小值,至少进行n-1次比较,然而继续在剩余的n-1个键值中选择出第二个小的值是否一定要进行n-2次比较呢?如果能利用钱n-1次比较所得信息,是否可以减少以后各次选中的次数比较呢?基本这个,我们来看堆排序,堆排序是指利用堆积树(堆)这种数据结构所设计的一种排序算法,利用数组的特点快速定位指定索引的元素。堆分为大根堆和小根堆,是完全二叉树。大根堆的要求是每个节点的值都不大于其父节点的值,即A[PARENT[i]] >= A[i]。在数组的非降序排序中,需要使用的就是大根堆,因为根据大根堆的要求可知,最大的值一定在堆顶。我们来看堆排序到底是怎么排的呢?下面我们以小堆为例,如下图所示:
如上图所示的序列是6、5、3、1、8、7、2、4,我们首先将其构建成一个堆,通过构建我们发现这个时候的序列为8、6、7、4、5、3、2、1,接着,我们1和8进行比较,发现1小于8,所以交互位置,刨去8,这个时候的序列为1、6、7、4、5、3、2,发现7比1大,交互位置,1比3小,交互位置,构成的是一个大顶堆了,这个时候,只需要7跟二叉树的最后一个节点进行比较即可,刨去7,依次类推,小编这里用语言描述的不是很准确,没有立体感,很难进行想象,小伙伴可以仔细看上面的这个动态图是如何进行堆排序的。
三、直接插入排序
常用的插入排序有两种,直接插入排序和希尔排序,首先我们来看直接插入排序,直接插入排序是一种简单的排序方法,她的基本思想是依次将每个记录插入到一个已排好序的有序表中去,从而得到一个新的、记录数增加1的有序表,就好比图书馆整理图书的这么一个过程,接着我们来看一下,直接插入排序的具体排序,如下图所示:
如上图所示的一组序列为6、5、3、1、8、7、2、4,首先6和5比较,6比5大交互位置,接着3和5比较,6比3大交互位置,3和5比,交互位置,现在的序列就是3、5、6、1、8、7、2、4,这个时候要把1插入到序列中,首先在徐磊中查找以确定1所应插入的位置,然后就行插入操作,从6起向左顺序查找,由于1小于3,所以1插入的位置就是3的前面,一般情况下,第i(i大于等于1)个记录进行插入操作时,R1、 R2,…,是排好序的有序数列,取出第i个元素,在序列中找到一个合适的位置并将她插入到该位置上即可。
/**
* 插入排序
*
* 从第一个元素开始,该元素可以认为已经被排序
* 取出下一个元素,在已经排序的元素序列中从后向前扫描
* 如果该元素(已排序)大于新元素,将该元素移到下一位置
* 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
* 将新元素插入到该位置中
* 重复步骤2
* @param numbers 待排序数组
*/
public static void insertSort(int[] numbers)
{
int size = numbers.length;
int temp = 0 ;
int j = 0;
for(int i = 0 ; i < size ; i++)
{
temp = numbers[i];
//假如temp比前面的值小,则将前面的值后移
for(j = i ; j > 0 && temp < numbers[j-1] ; j --)
{
numbers[j] = numbers[j-1];
}
numbers[j] = temp;
}
}四、希尔排序
希尔排序是一个基于插入排序的改进型插入排序算法。由于插入排序一次只能交换相邻的元素,因此元素只能一点点的从数组的一端移动到另一端。如果最小的元素在数组的末尾的话,那就需要N-1次移动,因此对于插入排序的效率是非常低的。
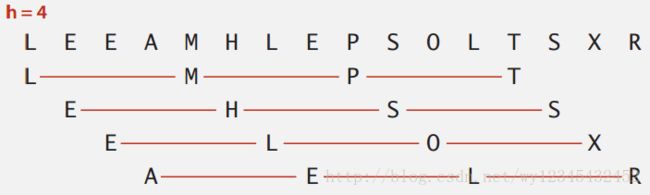
希尔排序的思想是使数组中任意间隔为h的元素是有序的。这样的数组也称为h有序数组,也即一个数组是h个互相独立的有序数组编制在一起组成的数组。如图所示为一个h有序数组包含了4个有序子数组。
上java代码:
public static void sort(Comparable[] a)
{
int N = a.length;
h = 1;
while(h < N/3) h = h*3 + 1;//步长可为1,4,13,40,121.......
while(h >= 1)
{
for (int i = h; i < N; i++)
{
for (int j = i; j >= h &&less(a[j], a[j - h]); j -= h)//函数less(a,b)比较a,b的大小,a
exch(a, j, j - h);//交换数组a中a[j],a[j-h]两个元素的位置
}
h = h/3;
}
} 五、冒泡排序
交换排序的基本思想是,比较两个记录键值的大小,如果这两个记录键值的大小出现逆序,则交换这两个记录,这样将键值较小的记录向序列前部移动,键值较大的记录向序列后部移动。首先我们来看交换排序中的第一种排序—冒泡排序,首先将第一个记录的键值和第二个键值进行比较,若为逆序,即R[1].key大于R[2].key,则将这两个记录交换,然后继续比较第二个和第三个记录的键值,依此类推,直到完成第n-1个记录和第n个记录的键值比较交换为止,上述过程称为第一趟起泡,其结果使键值最大的记录移到了第n个位置上,然后再进行第二趟起泡,即对前n-1个记录进行同样的操作,其结果是次大键值的记录安置在第n-1个位置上,重复上面的过程,当在一趟起泡过程中没有进行记录交换的操作时,整个排序过程终止,我们来看下面的一张图:
该方法的排序过程与气泡从水中往上冒的情况很相似,所以,美其名曰:冒泡排序,从上图我们可以很清楚的看出来,在排序的过程中,键值较小的记录好比气泡一样向上漂浮,键值较大的记录则向下沉。
/**
* 冒泡排序
* 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
* 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
* 针对所有的元素重复以上的步骤,除了最后一个。
* 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
* @param numbers 需要排序的整型数组
*/
public static void bubbleSort(int[] numbers)
{
int temp = 0;
int size = numbers.length;
for(int i = 0 ; i < size-1; i ++)
{
for(int j = 0 ;j < size-1-i ; j++)
{
if(numbers[j] > numbers[j+1]) //交换两数位置
{
temp = numbers[j];
numbers[j] = numbers[j+1];
numbers[j+1] = temp;
}
}
}
}六、快速排序
快速排序是交互排序的一种,实质上是对冒泡排序的一种改进,快速排序的基本思想是,在n个记录中取某一个记录的键值为标准,通常取第一个记录键值为基准,通过一趟排序将待排的记录分为小于或等于这个键值的两个独立的部分,这是一部分的记录键值均比另一部分记录的键值小,然后,对这两部分记录继续分别进行快速排序,以达到整个序列有序,我们来看图:
(a)一趟排序的过程:
(b)排序的全过程
把整个序列看做一个数组,把第零个位置看做中轴,和最后一个比,如果比它小交换,比它大不做任何处理;交换了以后再和小的那端比,比它小不交换,比他大交换。这样循环往复,一趟排序完成,左边就是比中轴小的,右边就是比中轴大的,然后再用分治法,分别对这两个独立的数组进行排序。
1.查找中轴(最低位作为中轴)所在位置
/**
* 查找出中轴(默认是最低位low)的在numbers数组排序后所在位置
*
* @param numbers 带查找数组
* @param low 开始位置
* @param high 结束位置
* @return 中轴所在位置
*/
public static int getMiddle(int[] numbers, int low,int high)
{
int temp = numbers[low]; //数组的第一个作为中轴
while(low < high)
{
while(low < high && numbers[high] > temp)
{
high--;
}
numbers[low] = numbers[high];//比中轴小的记录移到低端
while(low < high && numbers[low] < temp)
{
low++;
}
numbers[high] = numbers[low] ; //比中轴大的记录移到高端
}
numbers[low] = temp ; //中轴记录到尾
return low ; // 返回中轴的位置
}2、 递归形式的分治排序算法:
/**
*
* @param numbers 带排序数组
* @param low 开始位置
* @param high 结束位置
*/
public static void quickSort(int[] numbers,int low,int high)
{
if(low < high)
{
int middle = getMiddle(numbers,low,high); //将numbers数组进行一分为二
quickSort(numbers, low, middle-1); //对低字段表进行递归排序
quickSort(numbers, middle+1, high); //对高字段表进行递归排序
}
}七、归并排序
所谓的归并,是将两个或两个以上的有序文件合并成为一个新的有序文件,归并排序是把一个有n个记录的无序文件看成是由n个长度为1的有序子文件组成的文件,然后进行两两归并,如此重复,直至最后形成包含n个归并,得到n/2个长度为2或者1的有序文件,再两两归并,如此重复,直至最后形成包含n个记录的有序文件位置,这种反复将两个有序文件归并成一个有序文件的排序方法称为二路归并排序。二路归并排序的核心操作是将一堆数组中前后相邻的两个有序序列归并为一个有序序列,如下图所示:
八、基数排序
基数排序(radix sort)属于“分配式排序”(distribution sort),又称“桶子法”(bucket sort)或bin sort,顾名思义,它是透过键值的部份资讯,将要排序的元素分配至某些“桶”中,藉以达到排序的作用,基数排序法是属于稳定性的排序,其时间复杂度为O (nlog(r)m),其中r为所采取的基数,而m为堆数,在某些时候,基数排序法的效率高于其它的稳定性排序法。我们来看下面的一个例子:

八种内部排序的比较:
关于外部排序,下篇补充。