Unity 曲线插值(Hermite插值和Catmull_Rom插值)
1.三次Hermite样条
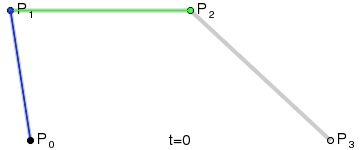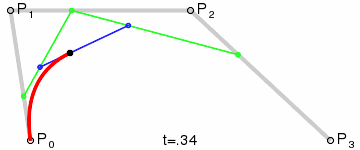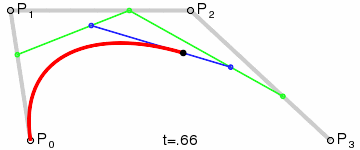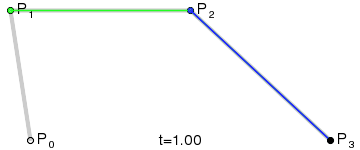
埃尔米特插值时颇为常用的插值算法,其根本也是三次贝塞尔曲线,有关贝塞尔曲线的知识可以参考这篇文章,有动图,看起来非常直观https://www.cnblogs.com/hnfxs/p/3148483.html下面是三次贝塞尔曲线模拟和公式
![]()
其中,P0和P3是一条曲线段的起点和终点,P1和P2是这个曲线段的两个外控制点。
三次Hermite差值实际上是贝塞尔曲线的转型,它将两个外控制点转成了两个切线,维基百科对Cubic Hermite spline解释比较清楚,贴上链接以供参考https://en.wikipedia.org/wiki/Cubic_Hermite_spline。下为三次Hermite 样条曲线的公式
![]() 转存失败重新上传取消,t∈[0,1]
转存失败重新上传取消,t∈[0,1]
P0和P1为曲线段的起点和终点,M0和M1为起点和终点的切线。
2.Catmull-Rom Spline
原理可参考http://www.dxstudio.com/guide_content.aspx?id=70a2b2cf-193e-4019-859c-28210b1da81f
![]() 转存失败重新上传取消
转存失败重新上传取消
注意,上图的四个点只能模拟出P1到P2,之间的曲线,在实际运用中,除了给的一组关键点以外,我们还需要给这组的收尾各添加一个点以画出整个曲线的第一个和最后一个曲线段。同样,贴上公式模拟P1到P2曲线的公式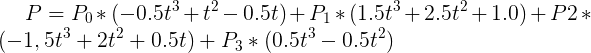
为了拟合P0到P1和P2到P3之间的曲线,我们需要在这几个曲线段外再取两个点,我的做法是取P1P0和P2P3两个向量计算出首位两个点。
3.样条曲线类
下面的代码段是一个完成的样条曲线类,可以直接使用,后面会贴上这个类的使用方式
// ==========================================
// 描述:
// 作者: HAK
// 时间: 2018-11-28 11:31:34
// 版本: V 1.0
// ==========================================
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
///
/// 样条类型
///
public enum SplineMode
{
Hermite, // 埃尔米特样条
Catmull_Rom, // Catmull_Rom 建议选择
CentripetalCatmull_Rom,// 向心Catmull_Rom
}
///
/// 样条曲线
///
public class SplineCurve
{
///
/// 曲线起始节点
///
private Node startNode;
///
/// 曲线终结点
///
private Node endNode;
///
/// 节点集合
///
private List nodeList;
///
/// 节点法线集合
///
private List tangentsList;
///
/// 曲线段集合
///
public List segmentList { get; private set; }
///
/// 曲线构造类型
///
public SplineMode mode { get; private set; }
public SplineCurve(SplineMode _mode = SplineMode.Catmull_Rom)
{
nodeList = new List();
tangentsList = new List();
segmentList = new List();
mode = _mode;
}
///
/// 添加首尾控制点
///
public void AddCatmull_RomControl()
{
if(mode != SplineMode.Catmull_Rom)
{
Debug.Log("不是Catmull样条");
return;
}
if(nodeList.Count < 2)
{
Debug.Log("Catmull_Rom样条取点要大于等于2");
return;
}
Node node = new Node(startNode.pos + (nodeList[0].pos - nodeList[1].pos), null, nodeList[0]);
nodeList.Insert(0, node);
node = new Node(endNode.pos + (endNode.pos - nodeList[nodeList.Count - 2].pos), nodeList[nodeList.Count - 1]);
nodeList.Add(node);
}
///
/// 添加节点
///
///
public void AddNode(Vector3 pos, float c)
{
Node node;
if(nodeList.Count < 1)
{
node = new Node(pos);
}
else
{
node = new Node(pos, nodeList[nodeList.Count - 1]);
}
nodeList.Add(node);
if(nodeList.Count > 1)
{
CurveSegement a = new CurveSegement(endNode, node,this);
a.c = c;
segmentList.Add(a);
CaculateTangents(segmentList.Count - 1); // 计算新加入的曲线段起始切线
}
else // 加入第一个节点
{
startNode = node;
}
endNode = node;
}
///
/// 获取点
///
///
///
public void GetPoint(int index, float t)
{
segmentList[index].GetPoint(t);
}
///
/// 获取切线
///
///
///
public void GetTangents(int index, float t)
{
segmentList[index].GetTangents(t);
}
///
/// 计算曲线段首尾切线
///
///
private void CaculateTangents(int index)
{
CurveSegement segement = segmentList[index];
if(index == 0)
{
segement.startTangents = segement.endNode.pos - segement.endNode.pos;
segement.endTangents = segement.endNode.pos - segement.startNode.pos;
return;
}
CurveSegement preSegement = segmentList[index - 1];
segement.startTangents = 0.5f * (1 - segement.c) * (segement.endNode.pos - preSegement.endNode.pos);
segement.endTangents = segement.endNode.pos - segement.startNode.pos;
preSegement.endTangents = segement.startTangents;
}
}
///
/// 曲线段
///
public class CurveSegement
{
///
/// 所属曲线
///
public SplineCurve rootCurve;
///
/// 曲线段起始位置
///
public Node startNode { get; private set; }
///
/// 曲线段末尾位置
///
public Node endNode { get; private set; }
public Vector3 startTangents;
public Vector3 endTangents;
///
/// 张力系数
///
public float c { get; set; }
public CurveSegement(Node _startNode,Node _endNode,SplineCurve _rootCurve)
{
startNode = _startNode;
endNode = _endNode;
rootCurve = _rootCurve;
c = -5f;
}
///
/// 获取点
///
///
///
/// 获取切线
///
///
///
/// 曲线节点
///
public class Node
{
///
/// 节点位置
///
public Vector3 pos;
///
/// 前连接节点
///
public Node preNode;
///
/// 后连接节点
///
public Node nextNode;
public Node(Vector3 _pos)
{
pos = _pos;
}
public Node(Vector3 _pos, Node _preNode, Node _nextNode = null)
{
pos = _pos;
if(_preNode != null)
{
preNode = _preNode;
_preNode.nextNode = this;
}
if(_nextNode != null)
{
nextNode = _nextNode;
_nextNode.preNode = this;
}
}
}
这个是我用 Catmull-Rom计算出来的点集结合Mesh绘图绘制出来的一条道路,拟合效果还算不错
最后贴上样条曲线类的使用,第一步创建,第二部加点,第三步添加首尾控制点,最后得到的path就是点集,大家可以遍历点集画线或者创建cube来观察曲线。
SplineCurve curve = new SplineCurve(); //新建曲线,默认为Catmull-Rom样条
curve.AddNode(point1); // 加入至少两个关键点
curve.AddNode(point2); // 代码里的AddNode还有以参数c,可以去掉,这是用来测试的
outCurve.AddNode(point3);
。。。
curve.AddCatmull_RomControl(); // 加入首位两个控制点
List path = new List();
for (int i = 0; i < outCurve.segmentList.Count; i++)
{
float add = 1f / 20; // 表示两个关键点之间取20个点,可根据需要设置
for (float j = 0; j < 1; j += add)
{
Vector3 point = centerCurve.segmentList[i].GetPoint(j);
path.Add(point);
}
}
曲线拟合本身就是一个公式,简单点写可以之间写成一个方法传进一组关键点返回一组点集,但是这样不利于扩展,也不利于对整个曲线上的每条曲线段进行单个控制。