决策树——绘图的全过程

以书上例子为基础（按照整个程序的调用顺序总结）：

首先列出树的数据，两组树的数据组成的列表，分别是listOfTrees[0]以及listOfTrees[1]：

def retrieveTree(i):
    listOfTrees =[{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
                  {'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
                  ]
    return listOfTrees[i]  

开始绘图，绘图函数：

def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])  #去除坐标轴显示,也可以选择显示哪些点，如plt.xticks([5,6]),或者ax1.set_xticks([5,6])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))    #plotTree是个函数，函数是对象可随时添加公共属性，totalW就是加入的一个属性，plotTree.totalW为叶节点的总数
    plotTree.totalD = float(getTreeDepth(inTree))   #plotTree.totalD树的深度，这两个是不变的全局变量，就表示整个树的深度和宽度
    plotTree.xOff = -0.5 / plotTree.totalW    
    plotTree.yOff = 1.0
    plotTree( inTree, (0.5, 1.0), '' )
    plt.show()

下面开始逐条分析上述函数及其对应的调用函数：

1.

fig = plt.figure(1, facecolor='white')

创建一个画布1，考虑到默认变量的全局性，必须指定1，方便下面的操作也在画布1上进行，底色设置为白色

2.

fig.clf()

清除之前的画布上的图像，这个跟内存有关系

3.

axprops = dict(xticks=[], yticks=[])

不显示坐标轴，有待解决

4.

createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)

createPlot是定义的函数名，是一个对象，只要是对象就可以定义公共属性，createPlot.ax1中的.ax1就是一个公共属性

5.

plotTree.totalW = float(getNumLeafs(inTree))

plotTree是定义的函数名，是一个对象，只要是对象就可以定义公共属性，createPlot.ax1中的.ax1就是一个公共属性，相当于是一个变量名，只要定义过的函数，都可以函数名.xxx作为变量名，这条程序调用了getNumLeafs函数，函数如下：

def getNumLeafs(myTree):   #获取叶节点数目
    numLeafs = 0
    firstStr = list( myTree.keys() )[0]    #把树转换成关键字列表，此时列表中只有一个关键字，因为是第一个分支点
    secondDict = myTree[firstStr]  #获取关键字（第一个问题）下的内容,至少有一个回答和一个结果，所以内容至少是｛0：1｝这样的形式
    for key in secondDict.keys():  #遍寻第一个问题的所有回答,即第一个关键字下的字典的关键字
        if type(secondDict[key]).__name__ == 'dict':  #判断下一级是不是还是字典， .__name__作用是将类型名称变为str
            numLeafs += getNumLeafs(secondDict[key])  #叶节点的数目等于所有最后一级的总数目
        else:                                         #比如第一个问题有2个分支，1个分支到底了+1，另一个分支又分出2个分支，2个分支都到底了，+2，一共是3
            numLeafs += 1                             #按程序步骤是，第一个关键字不符合if，+1，第二个关键字进入getNumLeafs(secondDict[key])，两个分支都不符合if，return2
    return numLeafs                                   #即getNumLeafs(secondDict[key])是2，最后结果是3

函数注意点：

myTree.keys()在Python3中不是list，而是dict_keys，需要用函list()转换成列表才能用位置标号取用

6.

plotTree.totalD = float(getTreeDepth(inTree))

这条程序调用了getTreeDepth函数，函数如下：

def getTreeDepth(myTree):    #获取树的层数
    maxDepth = 0
    firstStr = list( myTree.keys() )[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':   
            thisDepth = 1 + getTreeDepth( secondDict[key] )
        else:
            thisDepth = 1
        if thisDepth > maxDepth:    #key寻遍所有关键字，第一个关键字可能层数只有1，但是第二个可能是2层
                maxDepth = thisDepth    #加入一个比较，取层数最多的那个就是树的层数
    return maxDepth

7.

    plotTree.xOff = -0.5 / plotTree.totalW   
    plotTree.yOff = 1.0                      
    plotTree( inTree, (0.5, 1.0), '' )

难点分析参考下面这篇文章:

http://blog.csdn.net/qq_25974431/article/details/79083628

plotTree( inTree, (0.5, 1.0), '' )

调用时给的3个数据是，起始的完整树的数据，根的坐标（一定是在0.5，1.0位置），以及一个空的字符串，因为第一次画图实际上起点是(0.5,1.0)，终点也是(0.5,1.0)，在绘制树形图中，父级是起点，子级是终点，而树根自己到自己不需要字符，所以第三个参数给了空字符串

plotTree函数：

def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)    #获取当前节点下的叶节点总个数，后面递归myTree会变化
    depth = getTreeDepth(myTree)      #获取当前树的深度
    firstStr = list( myTree.keys() )[0]  #第一个问题，即获取树根
    cntrPt = ( plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff )
    #x轴的坐标由前一个位置确定当前位置，第一次是由初始位置确定
    plotMidText(cntrPt, parentPt, nodeTxt)   #父子之间加文本
    plotNode(firstStr, cntrPt, parentPt, decisionNode)  #指定文本内容，终点，起点，文本框类型
    secondDict = myTree[firstStr]  #提取字典下一层内容
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD   #树的深度往下走一级，树的深度不计算树根，y轴被分为plotTree.totalD，每层高度1.0 / plotTree.totalD
    for key in secondDict.keys():
        if type( secondDict[key] ).__name__ == 'dict':
            plotTree( secondDict[key], cntrPt, str(key) )  #递归，绘制下一层
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW   #如果不是字典，那肯定是一个节点，这个节点的x坐标位置距离上一个节点1.0 / plotTree.totalW
            plotNode( secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode )
            plotMidText( (plotTree.xOff, plotTree.yOff), cntrPt, str(key) )
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD

理解：

cntrPt = ( plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff )

这条程序是终点的坐标：x轴坐标为：前一个点X坐标 + (1 + 当前节点下的叶子节点总数) * 0.5 * 叶间距，其中0.5 * 叶间距就是半页距，可以理解为：  前一个位置x坐标 + （1+页节点个数） * 半页距       y轴坐标是当前的plotTree.yOff，用书上3.6的图为例，第一次是要确定树根的位置，x坐标是  -0.5*叶距 + （1+3）*半页距，y轴坐标是1，每下降一层，y轴坐标就减一层，树根不算入层数

下面调用plotMidText函数：

plotMidText(cntrPt, parentPt, nodeTxt)

def plotMidText(cntrPt, parentPt, txtString):  #起始点终止点之间的中点加文本
   #书上的写法啰嗦，(2,2)和(4,4)的重点直接(4+2)*0.5就行了，不用写成2+（4-2）*0.5
  
    xMid = ( parentPt[0] + cntrPt[0] ) / 2.0   #这样写更方便
    yMid = ( parentPt[1] + cntrPt[1] ) / 2.0
    fig = plt.figure(1)
    ax1 = fig.add_subplot(111,frameon=False)    
    ax1.set_xticks([])
    ax1.set_yticks([])

    ax1.text(xMid, yMid, txtString)    #在(xMid,yMid)位置加上文本内容txtString
                                       #text()作用：将文本放置在轴域的任意位置

在程序最前面定义的几个变量

decisionNode = dict( boxstyle = 'sawtooth', fc = '0.8' )  #boxstyle为文本框类型，sawtooth为锯齿形
leafNode = dict( boxstyle = 'round4', fc = '0.8' )        #round4为长方圆形，fc是边框线粗细
arrow_args = dict( arrowstyle = '<-' )                    #arrowstyle为箭头的样式

下面调用plotNode函数：

plotNode(firstStr, cntrPt, parentPt, decisionNode)  #树根是非叶节点，所以用decisionNode

def plotNode(nodeTxt, centerpt, parentPt, nodeType):
       
    fig = plt.figure(1)
    ax1 = fig.add_subplot(111, frameon=False)
    ax1.set_xticks([])
    ax1.set_yticks([])
    ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', xytext=centerpt,\
                 textcoords='axes fraction', va='center', ha='center', bbox=nodeType,\
                 arrowprops=arrow_args)

annotate括号中，nodeTxt是文本内容，xy是起点，xytext是终点，bbox是文本框类型，arrowprops是箭头类型，调用完后相当于完成了对树根的绘制

绘制完树根后下面进行数据的更新：

    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD  

获取第一层关键字下的内容，待会会用以判断是不是字典，并且树的深度往下走一层

运用循环递归绘制继续绘制：

    for key in secondDict.keys():
        if type( secondDict[key] ).__name__ == 'dict':
            plotTree( secondDict[key], cntrPt, str(key) )  #递归，绘制下一层
        else:
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW   #如果不是字典，那肯定是一个节点，这个节点的x坐标位置距离上一个节点1.0 / plotTree.totalW
            plotNode( secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode )
            plotMidText( (plotTree.xOff, plotTree.yOff), cntrPt, str(key) )

判断如果是字典的话，secondDict为第二层字典（  树至少是2个字典，{   问题1:{ 0:1, 1:0 }  }  ）

plotTree( secondDict[key], cntrPt, str(key) )  #递归，绘制下一层

递归时，之前的cntrPt终点被当作起点，即从树根出发的意思，str(key)则是要加在父子级之间的文本，key就是对树根的回答，要转化为字符串

plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW 
plotNode( secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode )
plotMidText( (plotTree.xOff, plotTree.yOff), cntrPt, str(key) )

如果不是字典，那这个回答下就是一个叶子节点，这个叶子节点的坐标距离上一个节点坐标的距离是一个叶间距，就是           （1/ 叶节点个数）这么大的距离，因为这个绘制的是第一个叶子节点的X坐标，上一个坐标是预先设定好的-0.5*页间距

然后设置样式，绘制该节点，并在父子级中点加入回答文本

最后加

plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD  #作用是y轴坐标回到上一层位置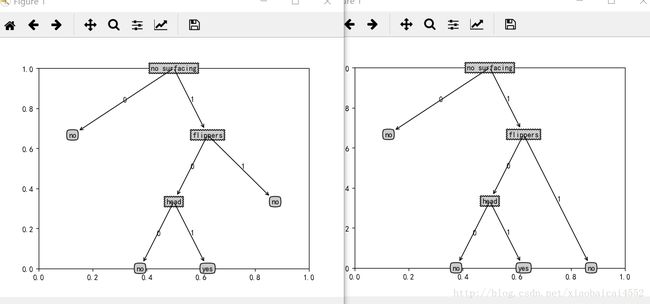

语句位置需要注意，是在循环外面，作用以2张图的对比来说明

画这张图的整个过程应该是第一个for循环画出第一层，第一层的第二个关键字下还是字典，所以是节点，递归画出第二层，先寻到关键字head，head关键字下的内容还是字典，所以递归进入第三层，遍寻后画出2个叶子节点，这个时候，在第二次递归后树的y轴已经到0了，如果在第二次递归的最后y轴不反回上一层，就会出现上图中右侧的情况，在第二次递归画完两个节点后，y轴返回上一层，然后进入第一次递归中寻到关键字no，是一个叶子节点，此时该次递归中两个key遍寻完了，在第一次递归中执行最后一条语句，y轴再返回上一层，第一次递归也结束了，此时非递归的2个key也遍寻完了，最后再执行一次非递归中的plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD，此时y的位置返回到1

最后如果要显示没有坐标没有边框的图，程序中每个定义图纸的地方都要如此写：

    fig = plt.figure(1)
    ax1 = fig.add_subplot(111, frameon=False)
    ax1.set_xticks([])
    ax1.set_yticks([])