线性回归之梯度下降法求解实践学习笔记（Python）

我通过简单、比较容易理解的一元线性回归为例，入门掌握机器学习、深度学习中基本概念和方法，例如梯度下降、代价函数、学习率等，以及与传统统计学不一样等思维和方法。

1. 关于线性回归

回归分析是研究相关关系的一种数学工具。他能帮助我们从一个变量取得的值去估计另一变量所取的值。例如人的身高与体重之间存在着关系，一般来说，人身高一些，则体重要重一些；再例如房价与房屋面积的关系，往往房屋面积大，房价高些。

1.1. 线性回归

在统计学中，线性回归是指：利用称为线性回归方程的最小平方函数，对一个或多个自变量和因变量之间关系进行建模的一种回归分析。线性回归方程的损失函数通常是通过最小二乘法，或者梯度下降法进行求解。

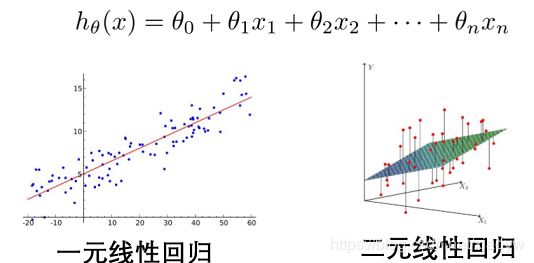
1、一元线性回归
两个变量（自变量、因变量）的关系用一条直线来模拟。
$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1$
这个方程对应的图像是一条直线，称作回归线。其中， ?1为回归线的斜率， ?0为回归线的截距，x为自变量。（附演示代码中：?1为k和k_grad，?0为b和b_grad）

2、多元线性回归
当Y值的影响因素不是唯一时，采用多元线性回归模型，$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1$模型如下所示：

1.2. 最小二乘

所谓最小二乘，其实也可以叫做最小平方和，其目的就是通过最小化误差的平方和，使得拟合对象无限接近目标对象。换句话说，最小二乘法可以用于对函数的拟合。

1.3. 标准方程法

一般线性回归公式表示为$y=w\cdot x+b$，利用矩阵的知识对线性公式进行整合：
对于只有两个特征（x1，x2）的时候的线性回归式子为$h_{\theta }(x)={\theta }_1{x}_1+{\theta }_2{x}_2$，假如有n个特征，则为$h_{\theta }(x)={\sum }_{i=1}^n{\theta }_i.x_i$，矩阵表达方式如下：

$$\left[\begin{array}{c}{\theta }_1\\ {\theta }_2\\ .\\ .\\ .\\ {\theta }_i\end{array}\right].\left[\begin{array}{cccc}{x}_1,& x_2,& ...& ,x_i\end{array}\right]=\sum _{i=1}^n{\theta }_i.x_i$$

我们把多项式求和化简为$h_{\theta }(x)={\theta }^T.x$，式子中除了w.x，还有一个参数b，也就是偏移量，或者叫误差项，误差项是真实值与预测值之间的差距，我们希望误差项越小越好。$h_{\theta }(x)={\theta }^T.x+\epsilon$。误差${\epsilon }^{(i)}$是独立并且具有相同的分布，并且服从均值为0方程为${\theta }^2$的高斯分布。

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(y_i-{\theta }^T{x}_i{)}^2$$

线性回归参数$\Theta =(X^{T}X{)}^{-1}{X}^{T}Y$

2. 机器学习之线性回归

2.1. 梯度下降

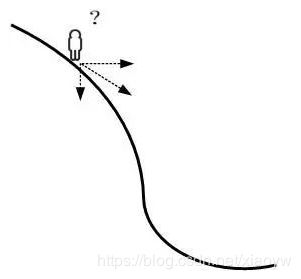
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要从山上下来（找到山的最低点，也就是山谷）。但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的地方走，然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

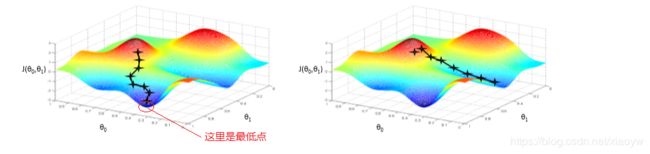
首先理解什么是梯度？通俗来说，梯度就是表示某一函数中该点处点方向导数沿着该方向取得最大值，即函数在当前位置的导数。属于优化算法。

2.2. 学习率

学习率(Learning rate)作为监督学习以及深度学习中重要的超参，其决定着目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。

学习速率是指导我们该如何通过损失函数的梯度调整网络权重的超参数。学习率越低，损失函数的变化速度就越慢。虽然使用低学习率可以确保我们不会错过任何局部极小值，但也意味着我们将花费更长的时间来进行收敛，特别是在被困在高原区域的情况下。

注：附代码中的lr为学习率。

2.3. 损失/代价函数

给定变量x，则拟合/预测函数输出一个f(x)，这个输出的f(x)与真实值y存在一定的误差，为了表示我们拟合的好坏，我们就用一个函数来度量拟合的程度，比如： $L(y-f(x))=(y-f(x){)}^2$，这个函数就称为损失函数(loss function)，或者叫代价函数(cost function)。损失函数越小，就代表模型拟合的越好。

注：损失函数与代价函数在概念定义上有微小差别，损失函数是指单组数据，代价函数是指数据集上的损失平均值，在机器学习上没有本质的差别，可以等同。

最小二乘法代价函数

对于一元线性回归方程：$h_{\theta }(x)={\theta }_0{x}_1+{\theta }_1{x}_2$，真实值为y，预测值为$h_{\theta }(x)$，找到合适的参数，使得误差平方和最小。
$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(y_i-h_{\theta }(x_i){)}^2$$

2.4. 用梯度下降法来求解线性回归

最小二乘法的求解，对最小二乘法代价函数$J({\theta }_0,{\theta }_1)$，求导$\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)$，使用泰勒展开式，例如j=1时，即对θ1求导。

$$j=0:\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})$$

$$j=1:\frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})\cdot x^{(i)}$$

重复直到收敛

repeat until convergence{
$${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})$$

$${\theta }_1:={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})\cdot x^{(i)}$$
}

上述公式中的α是学习率。

2.5. 梯度下降法与标准方程法比较

内容	梯度下降法	标准方程法
优点	当特征值非常多多时候也可以很好的工作	不需要学习率
		不需要迭代
		可以得到全局最优解
缺点	需要选择合适的学习率	需要计算$(X^{T}X{)}^{-1}$
	需要迭代很多个周期	时间复杂度大约是特征数量的立方
	只能得到最优解的近视值

3. 参考代码

'''
Created on 2019年2月16日
@author: 肖永威
'''
import matplotlib.pyplot as plt
import numpy as np

data = np.genfromtxt("data.csv", delimiter=",")
x_data = data[:,0]
y_data = data[:,1]
plt.scatter(x_data,y_data)
plt.show()

# 学习率learning rate
lr = 0.0001
# 截距
b = 0
# 斜率
k = 0
# 最大迭代次数
epochs = 50

# 最小二乘法
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
    return totalError / float(len(x_data)) / 2.0


def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
            k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
        # 每迭代5次，输出一次图像

    return b, k

print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
plt.plot(x_data, y_data, 'b.')
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

数据样本图及拟合结果：

Starting b = 0, k = 0, error = 2782.5539172416056
Running...
After 50 iterations b = 0.030569950649287983, k = 1.4788903781318357, error = 56.32488184238028

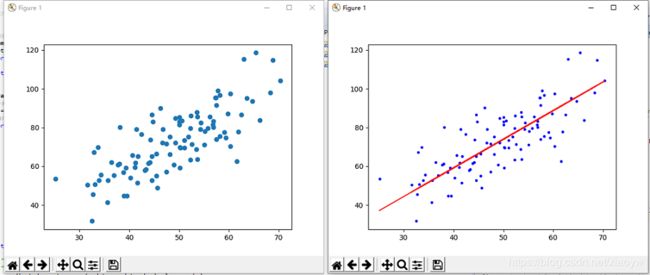
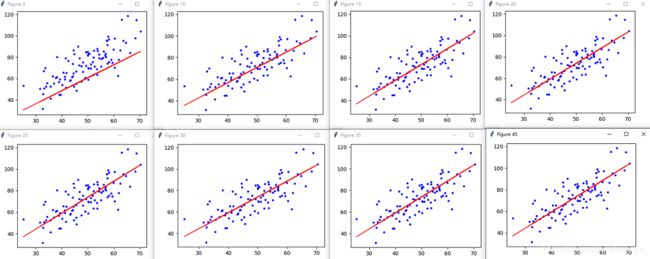
梯度下降，迭代过程图像如下：

参考：
《机器学习算法基础》 覃秉丰
《线性回归(最小二乘法)》 博客园 LeonHuo 2016.12