TensorFlow学习（九）：各种卷积网络

更新日志:

• 2017.5.13
  删除了一些不常用的内容,可以通过查文档获得,详细解释了conv2d的参数内容和运行过程

• 2017.12.26
  增加了空洞卷积(dilated Conv)的相关内容

• 2019.5.20
  所有代码和展示全部迁移到tensorflow 2.0

对于卷积网络的理论入门,可以看这篇博客:深度学习笔记五：卷积神经网络CNN(基本理论)

官方文档:Neural Network

查看全部的完整代码,可以去我的GitHub:LearningTensorFlow/CNN/

一.基本卷积操作

卷积操作有很多种，这部分主要是讲常见的在图像上面的卷积运算(conv2d)。也就是tf.nn.conv2d()这个函数。弄清楚二维卷积，其他的几种卷积比如一维卷积或者二维卷积等等都非常容易理解了。

在开始使用这个函数之前,首先要知道这代表是一个卷积运算,然后要知道,这个函数对于输入的格式有一些前提条件.如果了解了卷积的原理,这些输入的格式条件看上去还是很自然的,要是对于卷积的原理不了解,就会很不解.所以还是先把原理的基础打好,再来理解函数的使用. 至于这里没有讲到的其他卷积类型，可以看一下官方文档来理解。

Ⅰ.二维卷积

tf.nn.conv2d(input,filters,strides,padding,data_format=‘NHWC’,dilations=None,name=None)
作用：

• 对于给定的输入和滤波器tensor(注意,这里输入的滤波器参数都是4维的)计算二维卷积，其中输入的形状默认是[batch, in_height, in_width, in_channels]，滤波器/卷积核的形状是[filter_height, filter_width, in_channels, out_channels]，

参数:

• input: Tensor. 输入，元素必须是下面的类型: half, float32, float64.形状为[batch, in_height, in_width, in_channels]详细来说: batch就是一个batch的size，比如你同时丢100个样本什么的，in_height是样本的高，in_width就是样本的宽度，in_channels就是样本的通道数
• filter: 滤波器，和输入的类型需要是一样的。形状为[filter_height, filter_width, in_channels, out_channels] filter_height你可以形象的理解为一个滑动窗口的高度，filter_width就可以是一个滑动窗口的宽度，in_channels表示作用的输入的通道数（深度），所以你会发现他和input里面的最后一个参数in_channels应该是相同的，out_channels表示输出的feature map的深度，其实这里本质就是filter的个数。
• strides: 一个int类型或者一个int类型并且长度为1,2,4的列表，表明在各个维度上面滑动的步长，要是仅仅输入一个值，那么表明只在H和 W的步长，同时默认N和C着两个维度的步长为1
• padding: padding策略，分别是"SAME"或者"VALID"。
  data_format: 一个可选的字符串来指定输入的数据的格式，分别是 “NHWC”（默认）和"NCHW". "NHWC"表示的是数据的形状为 [batch, height, width, channels].,"NCHW"表明形状为 [batch, channels, height, width].
• dilations: 一个int类型或者一个int类型并且长度为1,2,4的列表, 默认是1，表示在各个维度上面的空洞因子。要是指定一个值，就是在H和W的维度的空掉率为这个值。同时默认N和C着两个维度的步长为1
• 名字: 操作名称，可选

要是这里看不懂的话，这里举一个例子来讲一下这个函数的功能。这里我们用tensorflow实现那个很出名的动图

代码:

import numpy as np
import tensorflow as tf

x=np.array([[[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0]],
            [[0,0,0],[0,1,2],[1,1,0],[1,1,2],[2,2,0],[2,0,2],[0,0,0]],
            [[0,0,0],[0,0,0],[1,2,0],[1,1,1],[0,1,2],[0,2,1],[0,0,0]],
            [[0,0,0],[1,1,1],[1,2,0],[0,0,2],[1,0,2],[0,2,1],[0,0,0]],
            [[0,0,0],[1,0,2],[0,2,0],[1,1,2],[1,2,0],[1,1,0],[0,0,0]],
            [[0,0,0],[0,2,0],[2,0,0],[0,1,1],[1,2,1],[0,0,2],[0,0,0]],
            [[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0],[0,0,0]]])


W=np.array([[[[1,-1,0],[1,0,1],[-1,-1,0]],
             [[-1,0,1],[0,0,0],[1,-1,1]],
             [[-1,1,0],[-1,-1,-1],[0,0,1]]],

            [[[-1,1,-1],[-1,-1,0],[0,0,1]],
             [[-1,-1,1],[1,0,0],[0,-1,1]],
             [[-1,-1,0],[1,0,-1],[0,0,0]]]])

print("input:\n")
print("x[:,:,0]:\n",x[:,:,0])
print("x[:,:,1]:\n",x[:,:,1])
print("x[:,:,2]:\n",x[:,:,2])

print("filter:")
print("W[0][:,:,0]:\n",W[0][:,:,0])
print("W[0][:,:,1]:\n",W[0][:,:,1])
print("W[0][:,:,2]:\n",W[0][:,:,2])
print("W[1][:,:,0]:\n",W[1][:,:,0])
print("W[1][:,:,1]:\n",W[1][:,:,1])
print("W[1][:,:,2]:\n",W[1][:,:,2])

#this
x=np.reshape(a=x,newshape=(1,7,7,3))
W=np.transpose(W,axes=(1,2,3,0))        #weights,[height,width,in_channels,out_channels]
print(W.shape)
b=np.array([1,0])                       #bias

input = tf.constant(value=x, dtype=tf.float32, name="input")
filter = tf.constant(value=W, dtype=tf.float32, name="filter")
bias = tf.constant(value=b, dtype=tf.float32, name="bias")
out=tf.nn.conv2d(input=input,filters=filter,strides=2,padding="VALID",name="conv2d")+bias

print(out[0][:,:,0])
print(out[0][:,:,1])

结果:

input:

x[:,:,0]:
 [[0 0 0 0 0 0 0]
 [0 0 1 1 2 2 0]
 [0 0 1 1 0 0 0]
 [0 1 1 0 1 0 0]
 [0 1 0 1 1 1 0]
 [0 0 2 0 1 0 0]
 [0 0 0 0 0 0 0]]
x[:,:,1]:
 [[0 0 0 0 0 0 0]
 [0 1 1 1 2 0 0]
 [0 0 2 1 1 2 0]
 [0 1 2 0 0 2 0]
 [0 0 2 1 2 1 0]
 [0 2 0 1 2 0 0]
 [0 0 0 0 0 0 0]]
x[:,:,2]:
 [[0 0 0 0 0 0 0]
 [0 2 0 2 0 2 0]
 [0 0 0 1 2 1 0]
 [0 1 0 2 2 1 0]
 [0 2 0 2 0 0 0]
 [0 0 0 1 1 2 0]
 [0 0 0 0 0 0 0]]
filter:
W[0][:,:,0]:
 [[ 1  1 -1]
 [-1  0  1]
 [-1 -1  0]]
W[0][:,:,1]:
 [[-1  0 -1]
 [ 0  0 -1]
 [ 1 -1  0]]
W[0][:,:,2]:
 [[ 0  1  0]
 [ 1  0  1]
 [ 0 -1  1]]
W[1][:,:,0]:
 [[-1 -1  0]
 [-1  1  0]
 [-1  1  0]]
W[1][:,:,1]:
 [[ 1 -1  0]
 [-1  0 -1]
 [-1  0  0]]
W[1][:,:,2]:
 [[-1  0  1]
 [ 1  0  1]
 [ 0 -1  0]]
(3, 3, 3, 2)
2019-05-20 19:53:08.888346: I tensorflow/core/platform/cpu_feature_guard.cc:142] Your CPU supports instructions that this TensorFlow binary was not compiled to use: AVX2
tf.Tensor(
[[ 1.  0. -3.]
 [-6.  1.  1.]
 [ 4. -3.  1.]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[-1. -6. -4.]
 [-2. -3. -4.]
 [-1. -3. -3.]], shape=(3, 3), dtype=float32)

是不是和图上的结果是一样的?现在来详细的讲一下这段代码.，载入什么包就不讲了,首先是定义了一个输入:

这个就是图中最左边的x了对吧,也就是说,这个就是我们的输入了.这里应该很好理解.

然后就是定义滤波器(“滑动窗口”)

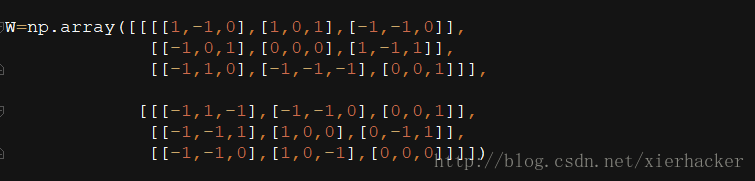
这个就是图像w的复现,照着做就是了,也是很简单的.

接下来就开始要注意的.
一开始定义的x的形状是什么呢?是7x7x3(高x宽x通道), 但是卷积操作这个函数需要的形状是4-D的,少了一维,少的那个维度就是batch,也就是样本数量.很简单,改变一下形状就行了.x=np.reshape(a=x,newshape=(1,7,7,3))于是就把原来的形状变为了1x7x7x3,这样就满足了函数的要求了.

然后就是w,w表示的是滤波器的参数,这个我们知道.但是我们定义w的时候,你看形状可以看出来是2x3x3x3(滤波器数量x高x宽x输入的通道),为什么这么写,是因为这么写是能够想到的最自然的写法了,很清晰.动图上面也是写么给出的.w[0]表示第一个滤波器,w[1]表示第二个滤波器…
但是!这样的格式不符合函数的要求,看前面函数参数的要求里面,这里滤波器的参数要是[filter_height, filter_width, in_channels, out_channels] 也就是说是(高x宽x输入通道x滤波器数量),这时候就用矩阵的转秩就行了,把第几个维度转到另外的维度
W=np.transpose(W,axes=(1,2,3,0))这句话之后,w就变成了函数要求的样子.把一开始的第0维转到了最后一维.

到这里,你其实可以根据理论算出来,这个输入和滤波器进行卷积之后的输入的形状.为1x3x3x2(样本数量x高x宽x通道数),你会发现,这里的样本数量是不变的,输入样本的数量是多少,这里还是多少(废话),中间的高和宽需要自己计算一下(不知道怎么算的可以看一下开头给出的博文).最后一个通道数其实就是卷积核的数量.要是理解的理论,这些还是很好理解的.

所以对于偏置的形状应当怎么设置呢?很简单,卷积核有n个,偏置的形状就是(n,).因为一个卷积核对应一个偏置,很容易就算出来了.比如这里的偏置b定为[1,0],因为有两个卷积核.

再讲一下卷积操作.

其他的简单就不说了,卷积那里,strides=[1,2,2,1],中间的两个表示一次横向移动和纵向移动的大小.在动图里面是2,那么这里设为2就行了.
padding=''VALID''表示不需要"加圈"

然后,大家应该对于这个卷积操作的函数会使用了.

二.池化操作（Pooling）

池化操作的思想算是比较简单的了.在上面博文的原理中也讲了.在这里,池化操作只详细讲一个平均池化的函数,因为其他的大概的思路功能参数都差不多,所以可以类比使用.
官方文档:Neural Network

列表:
tf.nn.avg_pool
tf.nn.max_pool
tf.nn.max_pool_with_argmax
tf.nn.avg_pool3d
tf.nn.max_pool3d
tf.nn.fractional_avg_pool
tf.nn.fractional_max_pool
tf.nn.pool

tf.nn.avg_pool(value, ksize, strides, padding, data_format=‘NHWC’, name=None)

作用：
在input上面执行average pooling
参数：
value: 一个4维tensor，形状为[batch, height, width, channels] 元素类型可以是 float32, float64, qint8, quint8, or qint32.
ksize: 整形列表,长度 >= 4. 表示窗口在输入的每个维度上面的尺寸.一般在二维的图像的情况下,都是[1,高,宽,1]
strides: 整形列表,长度 >= 4. 表示窗口滑动在输入tensor上面每个维度滑动的的步长.和卷积操作是一样的.
padding: 两种模式 ‘VALID’ 或者 ‘SAME’.
data_format: 两种模式 ‘NHWC’ 和 'NCHW’
name: 可选，操作名

到这里,基本你的卷积操作就讲完了,这些操作加上一些其他的基本操作,就可以组成更大更加复杂的卷积网络了.