深度学习经典算法 | 模拟退火算法详解
模拟退火算法基本思想
现代的模拟退火算法形成于20世纪80年代初,其思想源于固体的退火过程,即将固体加热至足够高的温度,再缓慢冷却。升温时,固体内部粒子随温度升高变为无序状,内能增大,而缓慢冷却时粒子又逐渐趋于有序,从理论上讲,如果冷却过程足够缓慢,那么冷却中任一温度时固体都能达到热平衡,而冷却到低温时将达到这一低温下的内能最小状态。
在这一过程中, 任一恒定温度都能达到热平衡是个重要步骤, 这一点可以用MonteCarlo算法模拟,不过其需要大量采样,工作量很大。但因为物理系统总是趋向于能量最低,而分子热运动则趋向于破坏这种低能量的状态,故而只需着重取贡献比较大的状态即可达到比较好的效果, 因而1953年Metropolis提出了这样一个重要性采样的方法, 即设从当前状态i生成新状态j.若新状态的内能小于状态i的内能(即Ej 1953年, Kirkpatrick把模拟退火思想与组合最优化的相似点进行类比, 将模拟退火应用到了组合最优化问题中,在把模拟退火算法应用于最优化问题时,一般可以将温度T当做控制参数,目标函数值f视为内能E,而固体在某温度T时的一个状态对应一个解。然后算法试图随着控制参数T的降低,使目标函数值f(内能E)也逐渐降低,直至趋于全局最小值(退火中低温时的最低能量状态),就像固体退火过程一样。 退火过程由一组初始参数, 即冷却进度表(cooling schedule) 控制, 它的核心是尽量使系统达到准平衡,以使算法在有限的时间内逼近最优解。冷却进度表包括: ①控制参数的初值T。:冷却开始的温度。 ②控制参数T的衰减函数:因计算机能够处理的都是离散数据,因此需要把连续的降温过程离散化成降温过程中的一系列温度点,衰减函数即计算这一系列温度的表达式。 ③控制参数T的终值T,(停止准则)。 ④Markov链的长度L.:任一温度T的迭代次数。 ①令T=T。,即开始退火的初始温度,随机生成一个初始解工,并计算相应的目标函数值E(x0)。 ②令T等于冷却进度表中的下一个值Ti。 ③根据当前,进行扰动(扰动方式可以参考后面的实例),产生一个新解、计算应的目标函数值E(),得到△E=E()一E()。 ④若△E<0,则新解被接受,作为新的当前解;若△E>0,则新解,按概率exp(一△E/) 接受,为当前温度。 ⑤在温度下,重复L,次的扰动和接受过程,即执行步骤③与④。 ⑥判断T是否已到达,是,则终止算法;否,则转到步骤②继续执行。 算法实质分两层循环,在任一温度随机扰动产生新解,并计算目标函数值的变化,决定是否被接受。由于算法初始温度比较高,这样,使E增大的新解在初始时也可能被接受.因而能跳出局部极小值,然后通过缓慢地降低温度,算法就最终可能收敛到全局最优解。还有一点要说明的是,虽然在低温时接受函数已经非常小了,但仍不排除有接受更差的解的可能,因此一般都会把退火过程中碰到的最好的可行解(历史最优解)也记录下来,与终止算法前最后一个被接受解一并输出。 为了更好地实现模拟退火算法,还需要注意以下一些方面。 上文已经提到过, 新解产生机制的基本要求是能够尽量遍及解空间的各个区域,这样、在某一恒定温度不断产生新解时,就可能跳出当前区域的极小以搜索其他区域,这是模拟退火算法能够进行广域搜索的一个重要条件。 收敛到全局最优的一般性条件是: ①初始温度足够高: ②热平衡时间足够长; ③终止温度足够低; ④降温过程足够缓慢。但上述条件在应用中很难同时满足。 (1)控制参数T的初值T。 求解全局优化问题的随机搜索算法一般都采用大范围的粗略搜索与局部的精细搜索相结合的搜索策略。只有在初始的大范围搜索阶段找到全局最优解所在的区域,才能逐渐缩小搜索的范围.最终求出全局最优解。模拟退火算法是通过控制参数T的初值T。和其衰减变化过程来实现大范围的粗略搜索和局部精细搜索。 一般来说,只有足够大的T。才能满足算法要求(但对不同的问题“足够大”的含义也不同,有的可能T。=100就可以,有的则要1010)。在问题规模较大时,过小的T。往往导致算法难以跳出局部陷阱而达不到全局最优。但为了减少计算量,T。不宜取得过大,而应与其他参数折中选取。 (2)控制参数T的衰减函数 衰减函数可以有多种形式,一个常用的衰减函数是 其中.a是一个常数,可以取为0.5~0.99,它的取值决定了降温的过程。小的衰减量可能导致算法进程迭代次数的增加,从而使算法进程接受更多的变换,访问更多的邻域,搜索更大范围的解空间,返回更好的最终解。同时由于在值上已经达到准平衡,则在时只需少量的变换就可达到准平衡。这样就可选取较短长度的Markov链来减少算法时间。 Markov链长度的选取原则是:在控制参数T的衰减函数已选定的前提下, 应能使在控制参数T的每一取值上达到准平衡。从经验上来说,对简单的情况可以令=100n,n为问题规模。 算法停止准则:对Metropolis准则中的接受函数分析可知,在T比较大的高温情况下,指数上的分母比较大,而这是一个负指数,所以整个接受函数可能会趋于1,即比当前解x,更差的新解工,也可能被接受,因此就有可能跳出局部极小而进行广域搜索,去搜索解空间的其他区域;而随着冷却的进行,T减小到一个比较小的值时,接受函数分母小了,整体也小了,即难以接受比当前解更差的解,也就是不太容易跳出当前的区域。如果在高温时,已经进行了充分的广域搜索,找到了可能存在最好解的区域,而在低温再进行足够的局部搜索,则可能最终找到全局最优了。因此,一般T,应设为一个足够小的正数,比如0.01~5,但这只是一个粗糙的经验,更精细的设置及其他的终止准则可以查阅文献。 函数: 《matlab在数学建模中的应用》其他一些参数的说明
算法基本步骤
几点说明
状态表达
SA算法中优化问题的一个解模拟了(或说可以想象为)退火过程中固体内部的一种粒子分布情况。这里状态表达即指实际问题的解(即状态)如何以一种合适的数学形式被表达出来,它应当适用于SA的求解、又能充分表达实际问题,这需要仔细地设计。可以参考遗传算法和禁忌搜索中编码的相关内容。常见的表达方式有:背包问题和指派问题的0-1编码, TSP问题和调度问题的自然数编码:还有用于连续函数优化的实数编码等。新解的产生
收敛的一般性条件
参数的选择
(3) Markov链长度
Python实现
import numpy as np
import matplotlib.pyplot as plt
import random
class SA(object):
def __init__(self, interval, tab='min', T_max=10000, T_min=1, iterMax=1000, rate=0.95):
self.interval = interval # 给定状态空间 - 即待求解空间
self.T_max = T_max # 初始退火温度 - 温度上限
self.T_min = T_min # 截止退火温度 - 温度下限
self.iterMax = iterMax # 定温内部迭代次数
self.rate = rate # 退火降温速度
#############################################################
self.x_seed = random.uniform(interval[0], interval[1]) # 解空间内的种子
self.tab = tab.strip() # 求解最大值还是最小值的标签: 'min' - 最小值;'max' - 最大值
#############################################################
self.solve() # 完成主体的求解过程
self.display() # 数据可视化展示
def solve(self):
temp = 'deal_' + self.tab # 采用反射方法提取对应的函数
if hasattr(self, temp):
deal = getattr(self, temp)
else:
exit('>>>tab标签传参有误:"min"|"max"<<<')
x1 = self.x_seed
T = self.T_max
while T >= self.T_min:
for i in range(self.iterMax):
f1 = self.func(x1)
delta_x = random.random() * 2 - 1
if x1 + delta_x >= self.interval[0] and x1 + delta_x <= self.interval[1]: # 将随机解束缚在给定状态空间内
x2 = x1 + delta_x
else:
x2 = x1 - delta_x
f2 = self.func(x2)
delta_f = f2 - f1
x1 = deal(x1, x2, delta_f, T)
T *= self.rate
self.x_solu = x1 # 提取最终退火解
def func(self, x): # 状态产生函数 - 即待求解函数
value = np.sin(x**2) * (x**2 - 5*x)
return value
def p_min(self, delta, T): # 计算最小值时,容忍解的状态迁移概率
probability = np.exp(-delta/T)
return probability
def p_max(self, delta, T):
probability = np.exp(delta/T) # 计算最大值时,容忍解的状态迁移概率
return probability
def deal_min(self, x1, x2, delta, T):
if delta < 0: # 更优解
return x2
else: # 容忍解
P = self.p_min(delta, T)
if P > random.random(): return x2
else: return x1
def deal_max(self, x1, x2, delta, T):
if delta > 0: # 更优解
return x2
else: # 容忍解
P = self.p_max(delta, T)
if P > random.random(): return x2
else: return x1
def display(self):
print('seed: {}\nsolution: {}'.format(self.x_seed, self.x_solu))
plt.figure(figsize=(6, 4))
x = np.linspace(self.interval[0], self.interval[1], 300)
y = self.func(x)
plt.plot(x, y, 'g-', label='function')
plt.plot(self.x_seed, self.func(self.x_seed), 'bo', label='seed')
plt.plot(self.x_solu, self.func(self.x_solu), 'r*', label='solution')
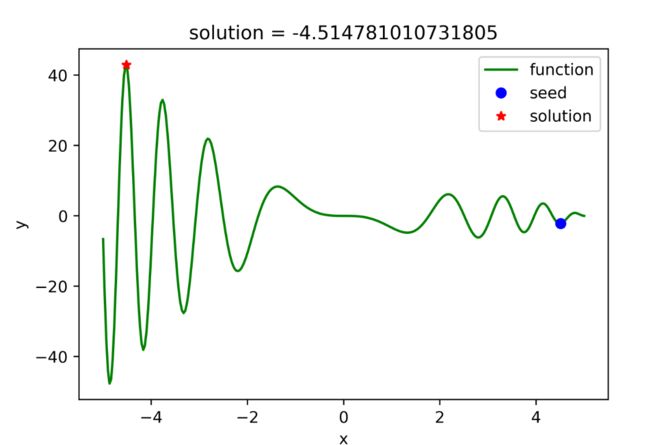
plt.title('solution = {}'.format(self.x_solu))
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.savefig('SA.png', dpi=500)
plt.show()
plt.close()
if __name__ == '__main__':
SA([-5, 5], 'max')
结果展示
参考文献