纯python实现多元回归（最小二乘法）

为什么会用纯Python来实现呢？这种陶（hao）冶（wu）情（yong）操（chu）的做法肯定也不是我自己闲着蛋疼搞着玩的。。。  明明有更好的科学计算库不用，非要纯手写正面硬刚，除了老师用挂科作为威胁还能有谁？

下面是一大纯手打的堆理推导... 写的逻辑有些混乱，后续有时间再慢慢整理 觉得麻烦的小伙伴就不用看了，反正我代码里也写的有注释，代码稍后传上github后更新连接

---------------------------------------------------------------------------------------------------------------
 

多元线性回归 最小二乘法实现

 

线性回归包括一元线性回归和多元线性回归，一元的是只有一个x和一个y。多元的是指有多个x和一个y。

 

 

对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。 选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小。有以下三个标准可以选择：

        （1）用“残差和最小”确定直线位置是一个途径。但很快发现计算“残差和”存在相互抵消的问题。
        （2）用“残差绝对值和最小”确定直线位置也是一个途径。但绝对值的计算比较麻烦。
        （3）最小二乘法的原则是以“残差平方和最小”确定直线位置。用最小二乘法除了计算比较方便外，得到的估计量还具有优良特性。这种方法对异常值非常敏感。

 

样本x为一个多维向量，x=[x1,x2,…xd]

那么权重W也是与X同维度的一个向量，W=[w1,w2,…wd]

所以Y对x的预测可以写为Y=W ∙ x+b(这里为内积的形式)，但通常将b移到W向量里面去，写为W=[b,w1,w2,…wd]，改变后的W用θ表示，θ=[θ0,θ1,θ2,…θd]

因为W的维度变了所以我们也要给x对应的多加一个维度，此时的x为[x0,x1,…xd]，使x0等于1，让其在矩阵相乘时匹配刚才在W中加入的b

现在Y=W ∙ x+b 就等价为 Y=θ∙x

在机器学习的矩阵运算当中，有个约定俗称的规定，当说某某向量时都指的是一个列向量，所以θ和x都是一个d+1维的列向量[θ0⋮θd]、[x0⋮xd]，同时也都是一个(d+1)x1维的矩阵

这里的维度就对应方程里面的元数，有几维就是几元

所以这里用大写的X表示有m个样本，X=[⋯x1T⋯⋯⋮⋯⋯xmT⋯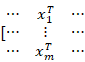]=[x01⋯xd1⋮⋯⋮x0m⋯xdm]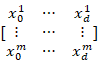，（这里的X是一个矩阵，包含了所有的样本点x1,x2,…xm而每一个样本点都是有相同的多维的， [⋯x1T⋯⋯⋮⋯⋯xmT⋯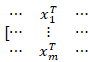]* [θ0⋮θd]= y0⋮ym=Y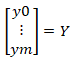，得到一个m*1维的矩阵Y，这个矩阵中的每一个参数代表给定的θ参数下对每一个样本xi的预测值yi，Y是对应样本的标签值，也是一个列向量。

得到Y（预测值）过后，就可以算损失函数了，L=i=1m（yi-yi）2，y是对应样本的真实值

L=（y1-y1）2+（y2-y2）2+…+（ym-ym）2

 =[ y1-y1,⋯,ym-ym] ∙ [y1-y1⋮ym-ym]

 =(y1,⋯,ym-[y1,⋯,ym]) ∙ [y1-y1⋮ym-ym]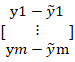

 =(x∙θ-Y)T ∙  (x∙θ-Y)

因为x、θ和Y都是一个m+1维的列向量所以第一项(x∙θ-Y)的结果也是一个列项量，所以加了一个转置

得到损失函数L=(x∙θ-Y)T (x∙θ-Y)，通过改变θ的值来最小化L

对θ求偏导，∂L∂θ=∂(θTxT-YT)(xθ-Y)∂θ=θTxTxθ-θTxTY-YTxθ+YTY∂θ，每一项都对θ求偏导然后加起来

 ∂L∂θ=2xTxθ-xTY-xTY，要使损失函数最小，就是偏导为0的点

所以推出xTxθ=xTY，θ=( xTx)-1xTY，这就要求(xTx)是可逆的

 

最小二乘法与梯度下降法的区别：

实现方法和结果不同：最小二乘法是直接对∆求导找出全局最小，是非迭代法。而梯度下降法是一种迭代法，先给定一个β ，然后向∆下降最快的方向调整β ，在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢，并且对初始点的选择极为敏感，其改进大多是在这两方面下功夫。