笔记：Inductive Robust Principal Component Analysis

Bao, B.K., et al., Inductive robust principal component analysis. IEEE Transactions on Image Processing, 2012. 21(8): p. 3794-3800.
本文针对经典的 Inductive Robust Principal Component Analysis 的理论方法进行展开详解。本人学术水平有限，文中如有错误之处，敬请指正。

摘要：RPCA 是一种直推式方法，并不能很好地处理新的样本。如果一个新的数据加入，RPCA需要重新计算所有的数据，导致非常高的计算代价。所以，RPCA 是一个不适用于在线计算（数据会分批按顺序加入）的应用。为了克服这个难题，此文提出了一个 inductive robust principal component analysis （IRPCA）方法，给定一组训练数据，和 RPCA 不同的是，（RPCA 旨在恢复原始数据矩阵），IRPCA 目标是学习一个潜在的投影矩阵，可以有效地去除数据中的损坏。

1 简介

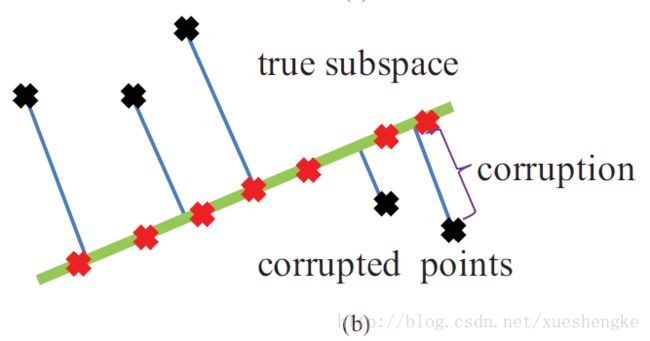
假设有一个误差修正的问题：数据组成部分如下

x=y+e,x∈Rd,(1)

其中 y 是低秩的子空间部分， e 是误差项。给定任意的数据向量 x ，求解的目标是从原始数据中分离出向量 y 和误差 e 。

上述问题等价于找出数据中的主成分，因为低秩的子空间可以被退化的高斯分布很好地建模。前提是误差服从小方差的高斯分布，广泛使用的主成分分析（PCA）可以有效地处理上述问题。有 n 个训练数据， X=[x1,x2,⋯,xn] ，PCA 通过最小化重建误差，来学习低秩投影，

minU ||X−UUTX||2F ,  s.t. UTU=Ir ,(2)

其中 Ir 是一个 r×r 的单位矩阵， ||⋅||2F 表示 Frobenious 范数， r 是 U 的秩（ U 的列数）。这个优化问题可以有效地用奇异值分解（SVD）求出。假设 U∗ 是从训练数据 X 求出的解，有了一个数据 x ，它的主成分可以估计出

y=U∗(U∗)Tx.(3)

这个方法计算很有效，而且稳定，使 PCA 被广泛用于误差修正。然而，在实际应用中，PCA 对严重的损坏效果很差，通常是偏离真实的子空间。

为了克服 PCA 的缺陷，Wright et al. 1 2 提出了 robust principal componen analysis (RPCA) ，成功应用于各个方面。
同样给定一组数据 X=[x1,x2,⋯,xn] ，RPCA 找到其主成分 Y=[y1,y2,⋯,yn] ，通过如下的凸优化问题

minY,E ||Y||∗+λ||E||1,  s.t. X=Y+E,(4)

其中 ||⋅||∗ 表示核范数（矩阵的奇异值之和）， ||⋅||1 表示 ℓ1 范数， λ 是权衡参数。假设损坏是足够稀疏的。这个稀疏假设是合理的、现实中普遍存在的。然而 RPCA 很难扩展已学习到的模型到新的数据上。可能处理测试数据的步骤： Y∗,E∗ 是从训练数据学习到的解，计算 Y∗ 的 SVD， Y∗=U∗Σ∗(V∗)T ；然后用 y=U∗(U∗)Tx 处理新数据。这个方法的实际效果很差。更具体来说， (Y∗,E∗)↔(U∗(U∗)TX,X−U∗(U∗)TX) 其实不接近，重构的解是不正确的。并且 E∗ 不是稀疏的。RPCA 不适用于在线计算的应用。

于是，此文提出了 inductive principal componen analysis (IRPCA)，不仅可以处理严重的损坏（相比于 RPCA），并且有良好的泛化能力。关键在于：从训练数据中学习出一个低秩投影，它能有效地移除误差，并把数据投影到其潜在的子空间中。

2 相关工作

Liu et al. 3 （基于 RPCA）提出了 low-rank representation (LRR) 模型

minZ,E ||Z||∗+λ||E||ℓ,  s.t. X=AZ+E,(5)

其中 A 是数据空间的字典， ||⋅||ℓ 根据具体情况选择合适的范数。如果 A=I ，那么 LRR 就变成了 RPCA 。子空间分割可以用 LRR 解决

minZ,E ||Z|∗+λ||E||2,1,  s.t. X=XZ+E,(6)

其中区别是 A=X ， ||E||2,1=∑nj=1∑di=1([E]ij)2−−−−−−−−−−√ 。这个方法也有 RPCA 同样的缺点：不能很好地处理新数据，需要重新计算，代价很高。

3 目标优化求解

3.1 模型建立

如果损坏没有任何的限制，那么 IRPCA 也是不实用的。比如，损坏是无序的，一般情况下没有简单的模型可以拟合它。幸运的是，IRPCA 是可行的。首先，即使损坏是乱序的，也能存在一个线性投影 P0 把数据投影到子空间中，能正确地恢复出数据（即使不是完全精确的恢复）；

其次，两个高维的向量，通常是独立的，近似是相互正交 4，也就是说，损坏通常不在正确的子空间中。这样的情况下， P0 严格地从数据中去除损坏。只要有数据 x ，其主成分就可以通过 y=P0x 获得。

开始建立优化模型，训练数据 X=[x1,x2,⋯,xn] 。目的是学习低秩投影 P0 ，给出如下优化函数

minP,E rank(P)+λ||E||0,  s.t. X=PX+E ,(7)

其中 λ 是系数， ||⋅||0 是 ℓ0 范数。该目标函数是不连续性的，因为 rank(⋅) 和 ℓ0 存在。根据通常的方法，采用核范数代替。同时， ℓ0 也用 ℓ1 代替。重新构建的凸的优化问题

minP,E ||P||∗+λ||E||1,  s.t. X=PX+E .(8)

假设最优解 P∗ 已经得到。对于一个新的数据 x ，我们估计其主成分 y=P∗x 和误差 e=x−P∗x ，计算很快速、简便。

3.2 优化求解

首先将上述问题转化为其转置的形式

minP,E ||PT||∗+λ||ET||1,  s.t. XT=PTXT+ET .(9)

根据论文 5 中提到，其计算复杂度是 O(d3) ，对高维数据代价更大。考虑到计算的效率，此文不直接求解该问题，而是到一个更简单的形式（参考 Theorem 1 6）： P∗ 总是在 X 的各列分布的字空间中。 P∗ 可以被分解为 P∗=L∗(Q∗)T ，其中 Q∗ 可以由正交化 X 的各列得到。于是，问题被转化为如下的形式

minL,E ||J||∗+λ||E||1,  s.t. X=LA+E, L=J,(10)

其中 A=(Q∗)TX ， ||⋅||∗ 表示核范数， ||⋅||1 表示 ℓ1 范数， λ 是权衡参数。

构建 Lagrangian 函数

L(L,E,J)= ||J||∗+λ||E||1+tr(YT1(X−LA−E))+tr(YT2(L−J))+μ2(||X−LA−E||2F+||L−J||2F),(11)

其中 Y1,Y2∈Rm×n 分别是 Lagrange 乘子矩阵， tr(⋅) 是迹函数， μ 是惩罚项系数（非变量）， ||⋅||F 表示 Frobenius 范数。显然，优化目标函数可以给出

(Lk+1,Ek+1,Jk+1)Y1k+1Y2k+1μ=argminL,E,J L(L,E,J,Y1k,Y2k),=Y1k+μ(X−LA−E),=Y2k+μ(L−J),=min(ρμ,μmax).

其中 ρ>1 是一个常数，用于不断增加 μ 的值。
由于优化目标函数中含有多个变量，通常的做法是每次最小化求解一个变量，而固定其他变量，之后更新 Lagrange 乘子，反复迭代直至收敛。论文使用经典的 inexact Augmented Lagrange Multiplier Method，也叫交替方向乘子法（Alternating Direction Multiplier Method），

Lk+1Ek+1Jk+1=argminL L(L,Ek,Jk,Y1k,Y2k),=argminE L(Lk+1,E,Jk,Y1k,Y2k),=argminJ L(Lk+1,Ek+1,J,Y1k,Y2k).(12)(13)(14)

迭代更新参数中还加入了 singular value thresholding (SVT) 和 shrinkage 操作，

Sα(x)=sign(x)⋅max{|x|−α, 0},(15)

其中 α>0 是一个设定的阈值。这是一个标量函数，对于矩阵或向量的操作都是 elementwise 的。
给出具体的迭代公式，推导过程见 Appendix，

Lk+1=((X−Ek)AT+Jk+Y1kAT−Y2kμ)(I+AAT)−1;Ek+1=Sλμ(X−Lk+1A+Y1kμ);(U,Σ,V)=svd(Lk+1+Y2kμ),Jk+1=US1μ(Σ)VT;(16)(17)(18)(19)

其中 Sα(⋅) 就是为了近似代替优化求解过程中的 ||J||∗+λ||E||1 而加入的；也就是说，在梯度求解 Lk+1,Ek+1,Jk+1 的过程中，并没有考虑这两项，而是用减去 Ek 的较小的元素值 Sλ/μ(Ek) ，和减去 Jk 的部分（较小的）奇异值 S1/μ(Σ) 来代替，直接求闭式解表达式。
优化步骤的迭代停止条件：

||X−Lk+1A−Ek+1||∞<ε and ||Z−Jk+1||∞<ε.(20)

其中 ||⋅||∞ 表示最大范数，定义为矩阵中最大的元素绝对值 ||A||∞=maxi,j{|aij|} 。

4 实验

略

Appendix

原论文中的公式有明显的符号错误。

1. 求解 Lk+1 , 当 ∂L∂L=0 时，（ ||J||∗+λ||E||1 与 L 无关）
   

   ∂L∂L∂L∂LLk+1=∂∂L{tr(YT1k(X−LA−Ek))+tr(YT2k(L−Jk))+μ2(||X−LA−Ek||2F+||L−Jk||2F)}=−Y1kAT+Y2k−μ(X−LA−Ek)AT+μ(L−Jk)=μL(I+AAT)+(Y2k−Y1kAT)+μ((Ek−X)AT−Jk),=0,=((X−Ek)AT+Jk+Y1kAT−Y2kμ)(I+AAT)−1.

2. 求解 Ek+1 , 当 ∂L∂E=0 时，（ ||J||∗ 与 E 无关， λ||E||1 用 Sλ/μ(⋅) 近似）
   

   ∂L∂E∂L∂EEk+1=∂L∂E{tr(YT1k(X−Lk+1A−E))+μ2||X−Lk+1A−E||2F}=−Y1k+μ(E+Lk+1A−X),=0,=Sλμ(X−Lk+1A+Y1kμ).

3. 求解 Jk+1 , 当 ∂L∂J=0 时，（ λ||E||1 与 J 无关， ||J||∗ 用 S1/μ(Σ), Σ=svd(⋅) 近似）
   

   ∂L∂J∂L∂J(U,Jk+1=∂L∂J{tr(YT2k(Lk+1−J))+μ2||Lk+1−J||2F}=−Y2k+μ(J−Lk+1),=0,Σ,V)=svd(Lk+1+Y2kμ),=US1μ(Σ)VT.

---

1. E. J. Candes, X. Li, Y. Ma, and J. Wright. (2009, Dec.). Robust Principal Component Analysis? [Online]. Available: http://wwwstat.stanford.edu/∼candes/papers/RobustPCA.pdf ↩
2. J. Wright, A. Ganesh, S. Rao, Y. Peng, and Y. Ma, “Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization,” in Proc. Neural Inf. Process. Syst., 2009, pp. 1–9. ↩
3. G. Liu, Z. Lin, and Y. Yu, “Robust subspace segmentation by low-rank representation,” in Proc. Int. Conf. Mach. Learn., 2010, pp. 1–8. ↩
4. R. R. Hamming, Art of Doing Science and Engineering: Learning to Learn. Boca Raton, FL: CRC Press, 1997, p. 364. ↩
5. G. Liu, Z. Lin, and Y. Yu, “Robust subspace segmentation by low-rank representation,” in Proc. Int. Conf. Mach. Learn., 2010, pp. 1–8. ↩
6. G. Liu, Z. Lin, S. Yan, J. Sun, Y. Yu, and Y. Ma. (2010). Robust Recovery of Subspace Structures by Low-Rank Representation [Online]. Available: http://arxiv.org/pdf/1010.2955.pdf ↩