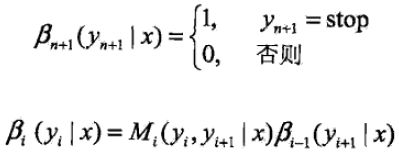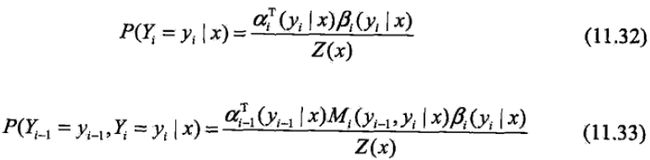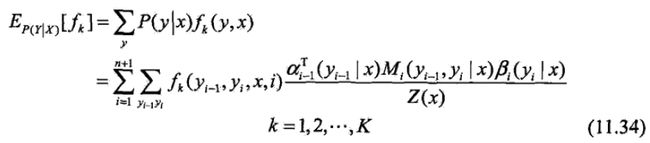条件随机场(CRF) - 3 - 概率计算问题
声明:
1,本篇为个人对《2012.李航.统计学习方法.pdf》的学习总结,不得用作商用,欢迎转载,但请注明出处(即:本帖地址)。
2,由于本人在学习初始时有很多数学知识都已忘记,所以为了弄懂其中的内容查阅了很多资料,所以里面应该会有引用其他帖子的小部分内容,如果原作者看到可以私信我,我会将您的帖子的地址付到下面。
3,如果有内容错误或不准确欢迎大家指正。
4,如果能帮到你,那真是太好了。
在之前的介绍中我们已近知道,条件随机场的概率计算问题是给定条件随机场P(Y|X),输入序列x和输出序列y,计算条件概率P(Yi=yi | x),P(Yi-1 =yi-1, Yi=yi | x)以及相应数学期望的问题。
为了方便起见,像隐马尔可夫模型那样,引进前向-后向向量,递归的计算以上概率及期望值。这样的算法称为前向-后向算法。
PS:前向-后向算法的详细讲解在我的“隐马尔可夫模型(HMM) - 2 - 概率计算方法”中已经做了总结,这里就不再详细说明了。
前向-后向算法
对每个指标i =0,1,...,n+1,定义前向向量ai(x):
递推公式为
又可表示为
ai(yi|x)表示在位置i的标记是yi并且到位置i的前部分标记序列的非规范化概率,若yi可取的值有m个,那ai(x)就是m维的列向量。
同样,对每个指标i =0,1,...,n+1,定义后向向量βi(x):
又可表示为
βi(yi|x)表示在位置i的标记为yi并且从i+1到n的后部分标记序列的非规范化的概率。
由前向-后向定义不难得到:
这里,若ai(x)是m维的列向量,那1就是元素均为1的m维列向量。
概率计算
按照前向-后向向量的定义,很容易计算标记序列在位置i是标记yi的条件概率和在位置i-1与i是标记yi-1和yi的条件概率:
其中,
Z(x)= anT(x)·1
期望值计算
利用前向-后向向量,可以计算特征函数关于联合分布P(X, Y)和条件分布P(Y | X)的数学期望。
特征函数fk关于条件分布P(Y |X)的数学期望是
其中,
Z(x)= anT(x)·1
假设经验分布为
则特征函数fk关于联合分布P(X, Y)的数学期望是
其中,
Z(x)= anT(x)·1
式11.23和式11.35是特征函数数学期望的一般计算公式。对于转移贴纸tk(yi-1, yi, x, i),k=1,2,...,K1,可以将式中的fk换成tk;对于状态特征,可以将式中的fk换成si,表示sl(yi, x, i),k = K1 +1,l = 1,2,...,K2。
有了式11.32 ~11.35,对于给定的观测序列x和标记序列y,可以通过一次前向扫描计算ai及Z(x),通过一次后向扫描计算βi,从而计算所有的概率和特征的期望。