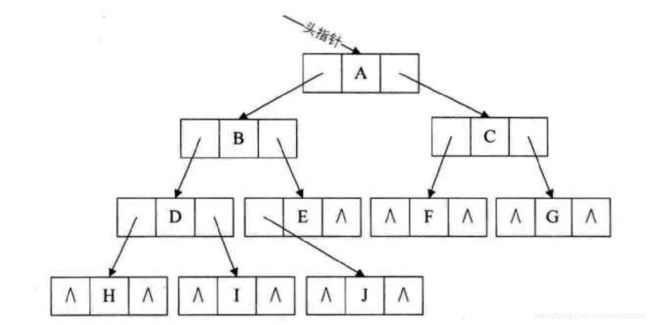
树
对树的小小归纳
- 树的存储
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法
- 二叉树
- 二叉树的性质
- 性质1
- 性质2
- 性质3
- 性质四
- 性质五
- 树的存储
- 顺序存储
- 二叉链表
- 遍历二叉树
- 前序遍历
- 中序遍历
- 层序遍历
- 树的建立
- 树与森林
- 树转化成二叉树
- 森林转换成二叉树
- 赫夫曼树和赫夫曼编码
- 赫夫曼树
- 赫夫曼编码
- 结束语
树的存储
因为之前就发过树的的概念啥的,所以这次就直接从树的存储开始。树的存储方式有不,我们来捋一捋(打字的时候发现的挺有趣的小东西:你能发现“一一”,“——”哪个是破折号吗1?另一个又是啥?哈哈哈)。
这里先讲一下:
上图中A是双亲,B、C是孩子,其中B是左子树,C是右子树。
双亲表示法
什么是双亲表示法呢,顾名思义,就是结点都存有它双亲的位置,同时为了可以很好的表示兄弟之间的关系,我们可以设置三个数据域:name、parents、rightchild分别用来存储自己的名称、自己的双亲,自己的右兄弟。没有双亲(根节点)就将parents数据域设为-1,没有有兄弟也将rightchild设为-1。然将其全部存进结构体数组中,结构体数组大致如下:
struct tree
{
char name;
int parents;
int rightchild;
}num[maxNum];//表示需要的数组长度
像上面的图,只需要定义一个结构体数组num[16]就可以存储所有的值。
like this(真的不想画表…):
| 下标 | name | parents | rightchild |
|---|---|---|---|
| 0 | A | -1 | -1 |
| 1 | B | 0 | 2 |
| 2 | C | 0 | -1 |
| 3 | D | 1 | 4 |
| 4 | E | 1 | -1 |
| 5 | F | 2 | 6 |
| 6 | G | 2 | -1 |
| 7 | H | 3 | 7 |
| 8 | I | 3 | -1 |
| 9 | J | 4 | 9 |
| 10 | K | 4 | -1 |
| 11 | L | 5 | 12 |
| 12 | M | 5 | 13 |
| 13 | N | 5 | -1 |
| 14 | O | 6 | 15 |
| 15 | P | 6 | -1 |
适当的为了节约时间,我们还可以再增加一些你需要的数据域,结构并不是一成不变的。
孩子表示法
这里先讲一个知识点 度 ,度就是结点的孩子的个数。例如上图A的度就是2,而F的度是3。
孩子表示法其实不难理解,就是把每个结点的孩子排列起来,以单链表作为存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中。

//孩子结点
typedef struct childnode
{
int num;
struct childnode* next;
} *CN;
//表头结构
typedef struct
{
int data;
CN firstchild;
}biaotou;
//树结构
typedef struct
{
biaotou nodes[MAX_SIZE];
int r,n;
}
这样的话,我们就可以从双亲出发,查看孩子的位置,但是如果要查找这个结点的双亲又该怎么办?其实,我们可以把双亲表示法和孩子表示法结合一下:
即多加一个parents数据域来存储该结点的双亲是谁,女少口阿!

孩子兄弟表示法
这种表示法从字面意思就可以知道是用孩子和兄弟的方式进行表示,比如一个结点,我们可以设置三个域,分别存储数据,它的孩子和它孩子的兄弟,如果没有就为空,这样上图就可以表示成为下面这种结构:

这个样子其实就像是二叉树,一个结点至多有两个孩子。
二叉树
因为之前写过二叉树的定义啥的,这里就直接从性质讲起吧。
二叉树的性质
性质1
在二叉树的第i层上至多有2i-1个结点(i>=1)。
我们用归纳法就很好的理解,也就是举个例子(当然这种东西直接就记吧)
性质2
深度为k的二叉树至多有2k-1个结点。
(深度其实就是二叉树的层数)其实不知道大家发现没有,这个跟我们高中生物学的遗传是真的很相像。如果大家能回忆起高中知识,那自然是好的,回忆不起,那我们就举个例子:
| 一层 | 个数 |
|---|---|
| 1 | 1(21-1) |
| 2 | 3(22-1) |
| 3 | 7(23-1) |
| 4 | 15 (24-1) |
性质3
对于任意一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。
其中,终端节点数就是叶子(没有孩子的结点)的结点数,我们来写一下它推导出来的过程。
我们记n0为终端结点数,n1为结点,n1代表度为1的结点,n2代表度为2的结点。所有的结点数用n表示。很明显,我们可以得到第一个式子:n=n0+n1+n2
要得到n0和n1的关系的关系,那我们再得到一个关于n的关系,我们看图不难可以发现,每条分支数+1就是结点数,因为把箭头指向的结点与那个箭头所代表的那条分支看作一个整体的话,A是没有指向它的箭头的分支,因此就有:n-1=n1+2n2。
两式联立,即可得出结论:n0=n2+1。
性质四
具有n个结点的完全二叉树的深度为[log2n]+1([x]代表步大于x的最大整数)
这里说的是完全二叉树,不是满二叉树,意思就是说这棵二叉树不一定是满的·,那么我们来推导一下:
在满二叉树的情形中,根据性质2有深度为n有2k-1个结点,即n=2k-1推出k=log2(n+1)。而当这棵树是完全二叉树时,同样的深度结点数肯定要比满二叉树要小或等,但同时肯定不小于比它小1的深度的满二叉树,因此我们得到了一个关系,即2k-1-1<=n<=2k-1。
最后处理得到上式结论。
性质五
如果对一棵有n个结点的完全二叉树(深度同性质四)按层序编号(每层从左到右),对于结点i(1<=i<=n):
1、如果i=1,则结点i时二叉树的根,无双亲;如果i>1,则其双亲时结点[i/2]([x]代表最大的整数)。
2、如果2i大于n,则i无左孩子(结点i为叶子结点);否则其左孩子时结点2i。
3、如果2i+1>n,则结点i无右孩子;否则其右孩子为2i+1。
先上个图
这三条都可以通过这个图验证,这里就不细说了。
树的存储
顺序存储
顺序存储顾名思义就是要将树的内容存储到一个顺序存储结构–数组中,还是用上图的那棵树:
用顺序存储结构就开辟一个8个空间的数组。
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | ^ |
空的用^表示,方法就是先把一个完全二叉树变成一棵满二叉树,那些不存在的子虚乌有的地方用 ^填充,代表为空。
二叉链表
二叉链表就是靠两个指针域分别连接左右孩子,然后一个数据域来存储自己的数据。
{
char neirong;
struct node *left;
struct node* right;
}
遍历二叉树
这里开始写二叉树的遍历方法,它分为四种:前序遍历,中序遍历、后序遍历和层序遍历。
不同的遍历次序会导致不同的路径。
我们先来看看前序遍历。
前序遍历
若二叉树为空,则空操作返回,否则先访问根节点,然后前序遍历左子树,再前序遍历右子树。
void qianxu()
{
//空操作返回
if(tree==NULL)
return;
printf("%c",neirong);
//从根结点开始先前序遍历左子树
qianxu(tree->left);
//再前序遍历右子树
qianxu(tree->right);
}
中序遍历
若树为空,则空操作返回,否则从根结点开始(不是访问根结点),中序遍历左子树,然后访问根结点,再中序遍历右子树。
void zhongxu()
{
//空操作返回
if(tree==NULL)
return;
//从根结点开始,只要他有左结点就一直递归向下进行
zhongxu(tree->left);
//没有孩子,打印该值
printf("%c",tree->neirong);
//开始遍历右孩子
zhongxu(tree->right);
### 后序遍历
**若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后时访问根结点。**
````c
void houxu()
{
//空操作返回
if(tree==NULL)
return;
//从根结点开始,只要他有左结点就一直递归向下进行
houxu(tree->left);
//只要他有左结点就一直递归向下进行
houxu(tree->right);
//没有孩子,打印该值
printf("%c",tree->neirong);
层序遍历
若树为空,则空操作返回,否则从树的第一层起,也就是根结点开始访问,从上到下逐层遍历,在同一层中按从左到右的顺序对结点逐个访问。
这个欢迎大佬告知一下
树的建立
树的建立也是一种递归。
void creatTree(Tree *tree)
{
char ch;
scanf("%c",&ch);
if(ch=='#')//我们假定输入‘#’为空
*tree=NULL
else
{
*tree=(Tree)malloc(sizeof(Tree));
(*tree)->neirong=ch;
creatTree(&(*tree)->left);
creatTree(&(*tree)->right);
}
}
树与森林
其实,在实际问题中,可能会有1对3或1对4或者更多的关系,比如我妈就有四个兄弟姐妹,这时候我们要把他们转化成二叉树,该怎么办呢?
树转化成二叉树
1.加线。在所有兄弟结点中加一条线。
2.去线。对树中每个结点,只保留他与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
3.层次调整。以树的根结点为轴心,将整棵树顺时针旋转一定角度,使之结构层次分明,注意第一个孩子是二叉树结点的左孩子,兄弟转换过来的孩子是右孩子。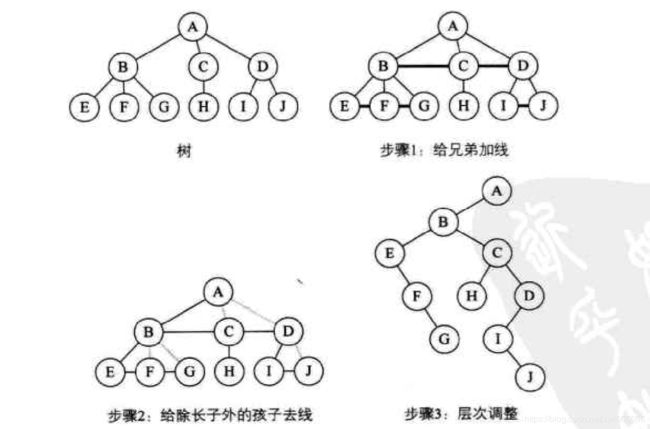
森林转换成二叉树
1、把每棵树转换成二叉树
2、第一棵二叉树不动,从第二棵二叉树开始,依次将后一棵二叉树的根结点作为前一棵二叉树的根结点的右孩子,用线连起来。
图片就不加了,看懂就行。
二叉树转换为树和森林就是反过来。
赫夫曼树和赫夫曼编码
赫夫曼树
似乎有些地方喜欢叫哈夫曼,我们这次就还是叫它赫夫曼吧哈哈。好了,还是回归正题。
什么是赫夫曼树?赫夫曼树其实就是去树的任何一个地方所花的代价最小的数,当然,这是整体上来看的。
如果要将百分制化为五分制,即A代表90 ~ 100,B代表80 ~ 89,C代表70 ~ 79,D代表60 ~ 69,E代表60分以下。
不用想,最先想到的就是用switch-case语句判断,用二叉树就是:

我们假定频率:60分以下0.3,60 ~70 为0.2,70 ~ 80为0.2,80 ~ 90 为0.25
,90 ~100 为0.05,上述这种我们计算一下要0.31+0.22+0.23+0.254+0.05*4=2.5。其实这很明显不是最简单的,因为80 ~ 90分段频率很大,可是他的判断次数最多,很不合理,那这时候我们就可以用赫夫曼的思想来解决问题。
赫夫曼的思路很简单:先拿出集合中最小的两个,将其组成一棵树,再用他们权值的和与剩下集合中最小的组成一棵树,直到集合空了。可能我这个表述不太好,没事,我用我的图来弥补一下,那上面成绩的来说,有这样一个集合{0.2,0.2,0.25,0.3,0.05}
我们首先将最小的两个组成一棵二叉树:
然后再与集合中最小的再组成一颗二叉树
以此类推,最后形成一颗赫夫曼二叉树
这就是最优化的呢,当然那两个0.2是可以换的,有时候可能会有不同种的赫夫曼树,但最后你算出来的结果一定会是一样的,有兴趣的可以试着构造一下{1,2,3,3}
赫夫曼编码
学完这里,原来压缩是这样的啊!
我们在打字,打中文的话,“的,了,是,在”这些字肯定使用的多,而打英文的话,元音字母“a,e,i,o,u”使用的多,那我们可不可以根据使用频率的多少来进行一些操作呢?
打个比方,我们知道一个含有八个比特,也就是要八个编码“0或1”组成,而如果有由a,b,c,d,e,f,g组成的七万个单词,普通的存储那就要七万个字节,五十六万个01,而如果我们把这七个单词用三位二进制表示(三位二进制可以表示8个字符,够了)那就只需要二十一万个01,那还有更少的方法,看到标题就知道,肯定是有的。
如果我们得知了这七个字母的频率,我们是不是可以列一个赫夫曼树(频率啥的就不假设了)。
这里我实在是懒了,要不我继续拿着ABCDE讲,其实少两个字母没事,理解了就行。
然后我们令左边为0,右边为1,就可把各个字母的编码写出来了,比如B的编码就是:01;C的编码就是:0001;而且赫夫曼树编码还有一个好处就是没有二义性。
比如,你不用赫夫曼树编码,自己创一套:
a:0
b:1
c:01
d:10
那如果给一串编码:01010,你觉得会是多少,是不是有很多种可能?而赫夫曼树就不会,因为赫夫曼树它的路径已经是分层的,是判断过后的,因而没有二义性。
结束语
哈哈,其实没啥好说的,就是让结构看起来完整点,好了好了,祝看到这篇文章的人天天开心,希望它能对你有所帮助,如果有什么不好的地方,敬请斧正,如果有问题,也可以一起探讨,蒟蒻一直都在哈哈哈!