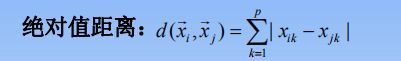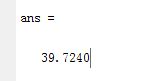聚类算法：K-means聚类与系统（层次）聚类SPSS操作

笔记整理来自清风老师的数学建模课程： https://www.bilibili.com/video/BV1gJ411k7X4?from=search&seid=15370102798756305377

目录

1. 聚类模型的概念

2. K-means聚类算法（K均值）

2.1 步骤

 2.2 评价

3. K-means++ 算法

3.1 算法步骤

4. 例题讲解——K-means算法

4.1 K-mean算法步骤

4.1.1 导入数据

4.1.2  SPSS操作

4.2 结果分析

 4.3 K-means算法的讨论

4.3.1 聚类个数确定与量纲不一致问题

4.3.2 Z标准化（无量纲化）SPSS操作步骤

 5. 系统聚类（层次聚类）

5.1 系统聚类原理

5.1.1 例题1：根据成绩，对学生进行分类

 5.1.1 例题2：根据成绩，对课程进行分类

 5.1.3  例题3 ：根据月人均消费对省进行分类

 5.1.4 类与类之间的距离

5.2 最短距离系统聚类法

 5.3 最长距离系统聚类法

 5.4 聚类分析需要注意的问题

6. SPSS操作步骤——系统聚类

 6.1 系统聚类算法流程

6.2 SPSS操作步骤

 6.3 结果分析

6.4 系统聚类算法的优缺点

---

1. 聚类模型的概念

“物以类聚，人以群分”，所谓的聚类，就是将样本划分为由类似的对象组成的多个类的过程。

聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测； 也可以探究不同类之间的相关性和主要差异。

 

聚类和上一讲分类的区别：分类是已知类别的，聚类未知

 

 

2. K-means聚类算法（K均值）

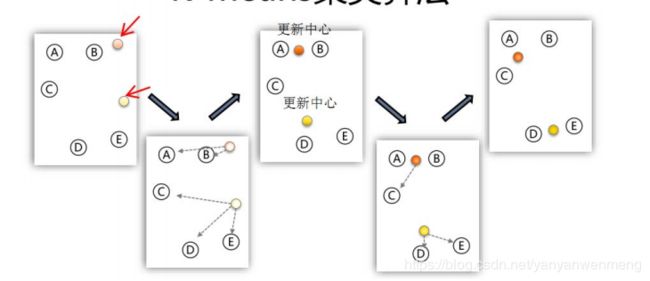
2.1 步骤

1. 指定需要划分的簇[cù]的个数K值（类的个数）;   一个类也叫一个簇。
2. 随机地选择K个数据对象作为初始的聚类中心 （不一定要是我们的样本点）;   K个数据对象不一定是样本，可以为随机的数据
3. 计算其余的各个数据对象到这K个初始聚类中心 的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中;
4. 调整新类并且重新计算出新类的中心;   类的中心有点像样本的重心
5. 循环步骤三和四，看中心是否收敛（不变），如 果收敛或达到迭代次数则停止循环;
6. 结束。

https://www.naftaliharris.com/blog/visualizing%E2%80%90k%E2%80%90means%E2%80%90clustering/

算法流程图：

 2.2 评价

优点：

（ 1 ）算法简单、快速。

（ 2 ）对处理大数据集，该算法是相对高效率的。

缺点：

（ 1 ）要求用户必须事先给出要生成的簇的数目 K 。

（ 2 ）对初值敏感。

（ 3 ）对于孤立点数据敏感。

K‐means++ 算法可解决 2 和 3 这两个缺点。

 

3. K-means++ 算法

K-means++算法选择初始聚类中心的基本原则是：初始聚类中心之间的相互距离要尽可能的远。

3.1 算法步骤

算法描述如下：（只对K-mean算法“初始化K个聚类中心”这一步进行了优化）

步骤一： 随机选取一个样本作为第一个聚类中心；

步骤二： 计算每个样本与当前已有聚类中心的最短距离（即与最 近一个聚类中心的距离），这个值越大，表示被选取作为聚类中 心的概率较大；最后，用轮盘法（依据概率大小来进行抽选）选 出下一个聚类中心；

步骤三： 重复步骤二，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了。

 

4. 例题讲解——K-means算法

比如现在需要对省份进行聚类，看看哪些省份的消费习惯比较接近。数据如下：

数据来源：嵩天Python机器学习算法课程案例

 

省份	食品	衣着	家庭设备	医疗	交通	娱乐	居住	杂项
北京	2959.19	730.79	749.41	513.34	467.87	1141.82	478.42	457.64
天津	2459.77	495.47	697.33	302.87	284.19	735.97	570.84	305.08
河北	1495.63	515.9	362.37	285.32	272.95	540.58	364.91	188.63
山西	1406.33	477.77	290.15	208.57	201.5	414.72	281.84	212.1
内蒙古	1303.97	524.29	254.83	192.17	249.81	463.09	287.87	192.96
辽宁	1730.84	553.9	246.91	279.81	239.18	445.2	330.24	163.86
吉林	1561.86	492.42	200.49	218.36	220.69	459.62	360.48	147.76
黑龙江	1410.11	510.71	211.88	277.11	224.65	376.82	317.61	152.85
上海	3712.31	550.74	893.37	346.93	527	1034.98	720.33	462.03
江苏	2207.58	449.37	572.4	211.92	302.09	585.23	429.77	252.54
浙江	2629.16	557.32	689.73	435.69	514.66	795.87	575.76	323.36
安徽	1844.78	430.29	271.28	126.33	250.56	513.18	314	151.39
福建	2709.46	428.11	334.12	160.77	405.14	461.67	535.13	232.29
江西	1563.78	303.65	233.81	107.9	209.7	393.99	509.39	160.12
山东	1675.75	613.32	550.71	219.79	272.59	599.43	371.62	211.84
河南	1427.65	431.79	288.55	208.14	217	337.76	421.31	165.32
湖南	1942.23	512.27	401.39	206.06	321.29	697.22	492.6	226.45
湖北	1783.43	511.88	282.84	201.01	237.6	617.74	523.52	182.52
广东	3055.17	353.23	564.56	356.27	811.88	873.06	1082.82	420.81
广西	2033.87	300.82	338.65	157.78	329.06	621.74	587.02	218.27
海南	2057.86	186.44	202.72	171.79	329.65	477.17	312.93	279.19
重庆	2303.29	589.99	516.21	236.55	403.92	730.05	438.41	225.8
四川	1974.28	507.76	344.79	203.21	240.24	575.1	430.36	223.46
贵州	1673.82	437.75	461.61	153.32	254.66	445.59	346.11	191.48
云南	2194.25	537.01	369.07	249.54	290.84	561.91	407.7	330.95
西藏	2646.61	839.7	204.44	209.11	379.3	371.04	269.59	389.33
陕西	1472.95	390.89	447.95	259.51	230.61	490.9	469.1	191.34
甘肃	1525.57	472.98	328.9	219.86	206.65	449.69	249.66	228.19
青海	1654.69	437.77	258.78	303	244.93	479.53	288.56	236.51
宁夏	1375.46	480.89	273.84	317.32	251.08	424.75	228.73	195.93
新疆	1608.82	536.05	432.46	235.82	250.28	541.3	344.85	214.4

4.1 K-mean算法步骤

4.1.1 导入数据

4.1.2  SPSS操作

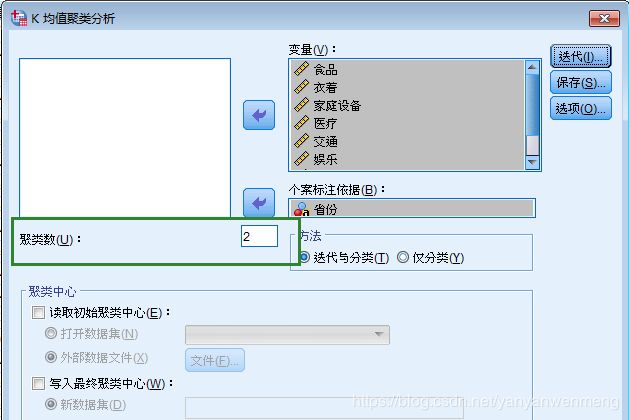
第一步：选择【分析】【分类】【K-means聚类】

第二步：【变量】相当于指标，【个案标注依据】相当于分类依据。聚类数我们需要分为聚类就填几类。

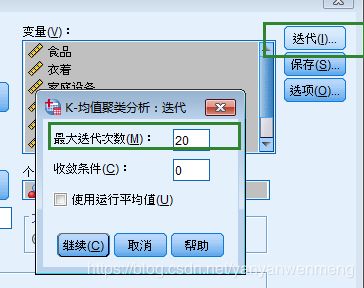
第三步：【迭代次数】可以调大一些，默认为10次。K均值聚类是不断进行迭代的，如果到达了最大迭代次数还未收敛，就结束了，所以需要调大一些，保证尽量收敛。

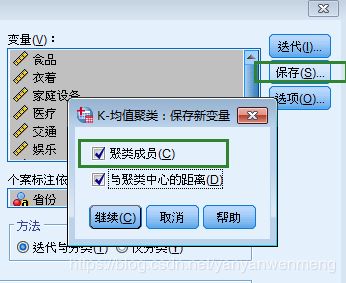
 第四步：【聚类成员】可以生成一个变量，表明这个城市是属于哪一类的。

第五步：勾选上【每个个案的聚类信息】

4.2 结果分析

说明初始的聚类中心为上海和内蒙古。

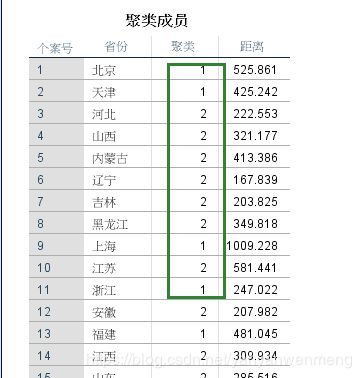
 1、2代表聚类的类别。比如北京、天津、上海分为了第一类，河北、山西等地方分为了第二类。

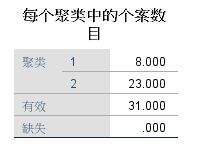
代表分为第一类的有8个城市，分为第2类的有23个城市。 

 4.3 K-means算法的讨论

4.3.1 聚类个数确定与量纲不一致问题

（ 1 ）聚类的个数 K 值怎么定？

答：分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个 K 值， 看分成几类的结果更好解释，更符合分析目的等。

 【看哪个好解释就取哪个k】

（ 2 ）数据的量纲不一致怎么办？

答：如果数据的量纲不一样，那么算距离时就没有意义。例如：如果 X1 单位是米，X2 单位是吨，用距离公式计算就会出现“米的平方”加上“吨的平方” 再开平方，最后算出的东西没有数学意义，这就有问题了。

【比如上面的例题单位都是元，所以量纲是一致的。如果单位不一致，需要进行无量纲化】

 

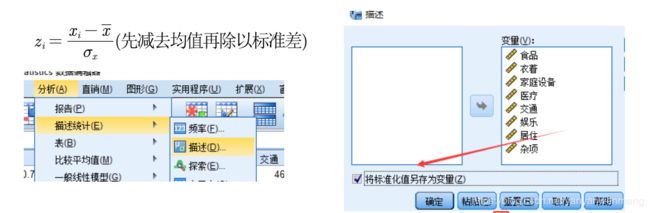
标准差

4.3.2 Z标准化（无量纲化）SPSS操作步骤

第一步：选中需要进行Z标准化的数据，选中【分析】【描述统计】【描述】

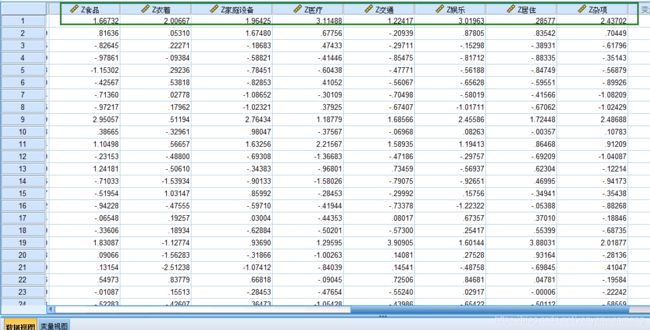
第二步：将需要标准化的变量放入【变量】中，勾选【将标准化值另存为变量】。

在【数据视图】中就可以得到Z标准化后的结果了。后面变量选择的时候就可以选择Z标准化后的值了。

 5. 系统聚类（层次聚类）

系统聚类不需要事先给定K值。

5.1 系统聚类原理

系统聚类的合并算法通过计算两类数据点间的距离，对 最为接近的两类数据点进行组合，并反复迭代这一过程，直 到将所有数据点合成一类，并生成聚类谱系图。

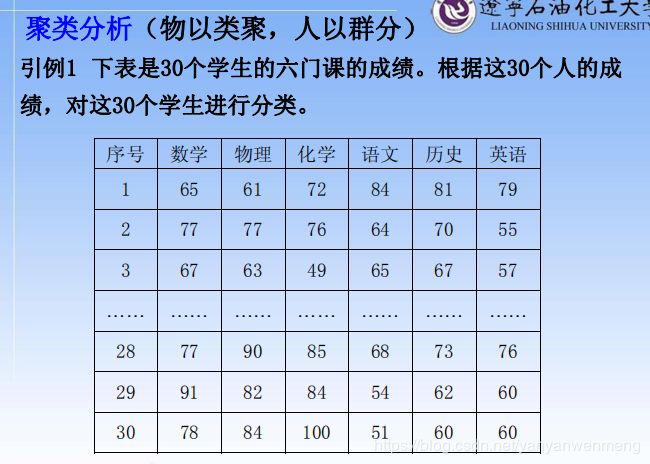
5.1.1 例题1：根据成绩，对学生进行分类

对样本进行分类

步骤：

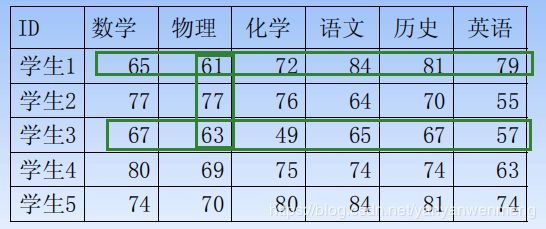
第一步：只考虑数学成绩。

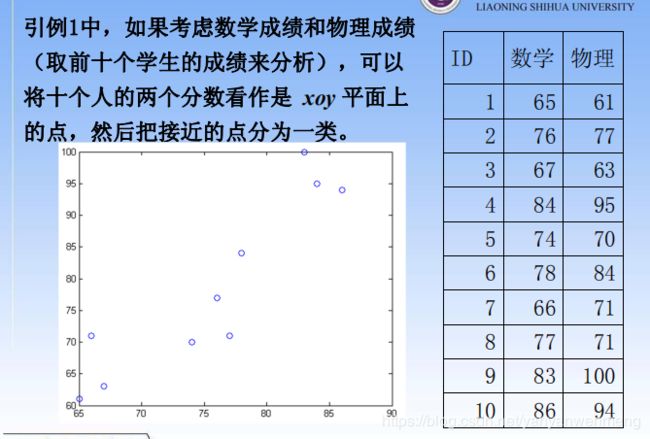
第二步：只考虑数学和物理成绩 

 【分类准则】距离近的样本聚为一类

 

 样本与样本之间的常用距离。

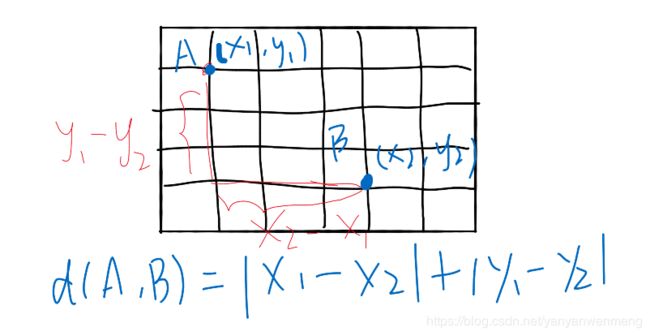
绝对值距离：一般用于网状道路。

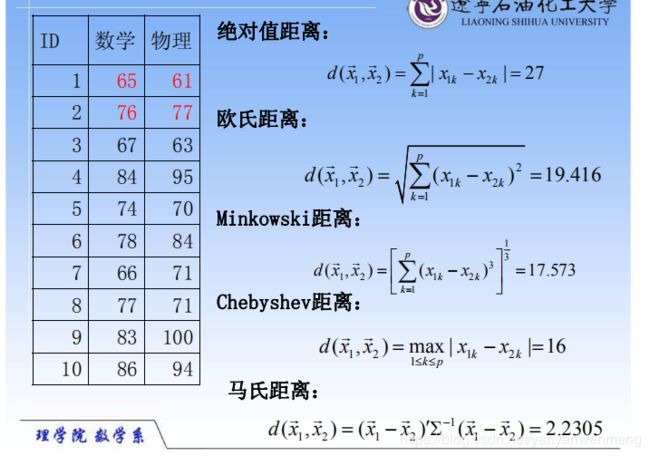
 欧式距离(除了网格中用的绝对值距离，基本大多数情况用的都是欧式距离）

实例计算：65（X），61(Y）

 

 

 5.1.1 例题2：根据成绩，对课程进行分类

对指标进行分类

指标与指标间的距离（对指标进行分类时才需要计算之间间的距离）：

 

 

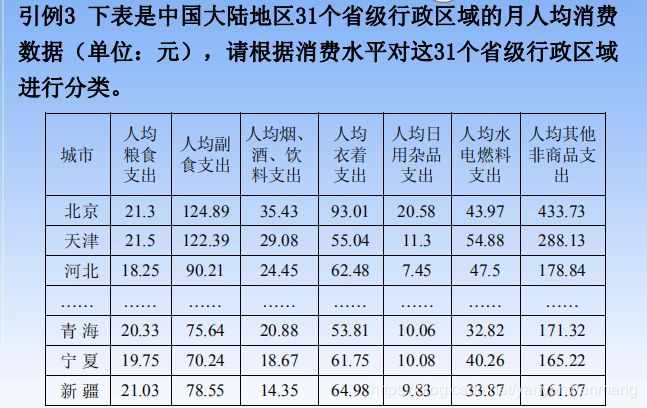
 5.1.3  例题3 ：根据月人均消费对省进行分类

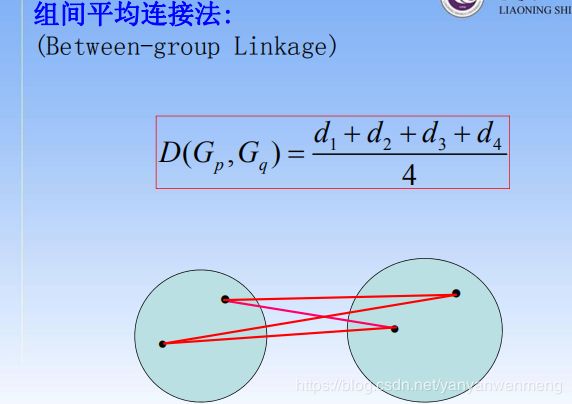
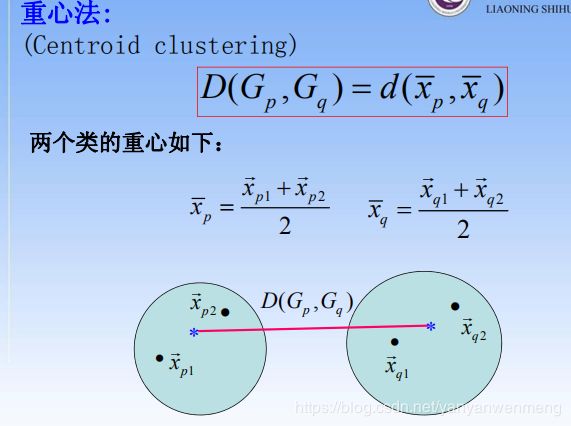
 5.1.4 类与类之间的距离

 

 

 

一般默认使用的位重心法 。

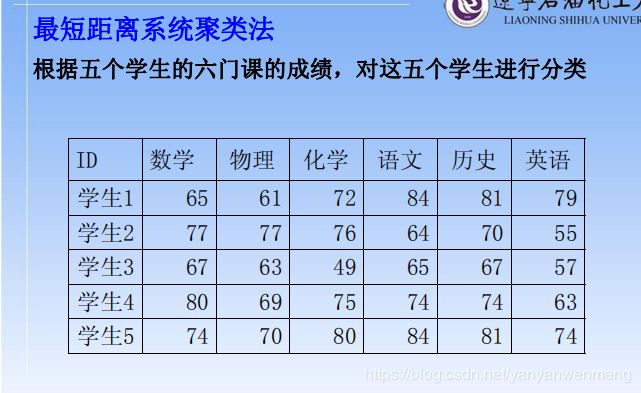
5.2 最短距离系统聚类法

 样本1和2之间的距离

sqrt((65-77)^2+(61-77)^2+(72-76)^2+(84-64)^2+(81-70)^2+(79-55)^2)

 样本1和3之间的距离（G31=G13=39.7）：第一行和第3行对应的数相减，求欧式距离即可。

 sqrt((65-67)^2+(61-63)^2+(72-49)^2+(84-65)^2+(81-67)^2+(79-57)^2)

样本5和3之间的距离（第5行第3列）：G53=43.6 

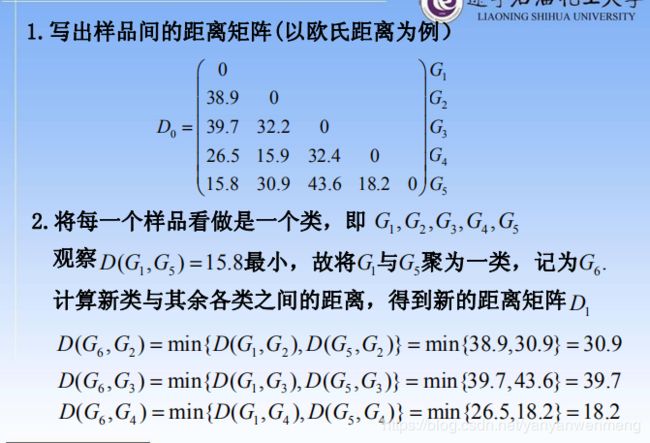
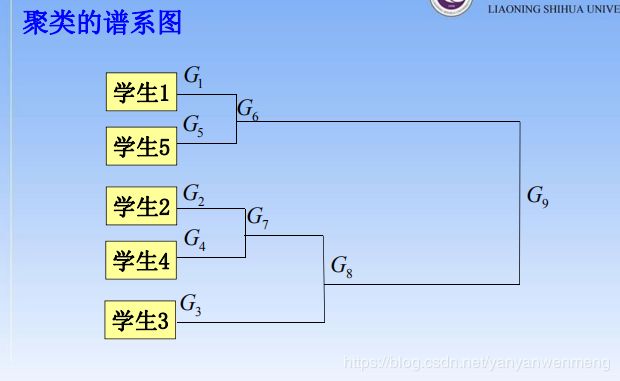
根据欧式距离，发现G1和G5间的距离最短：

首先将G1和G5聚为一类，命名为G6

计算各类（G6、G2、G3、G4）与新类G6之间的距离，发现G2和G4的距离最短：

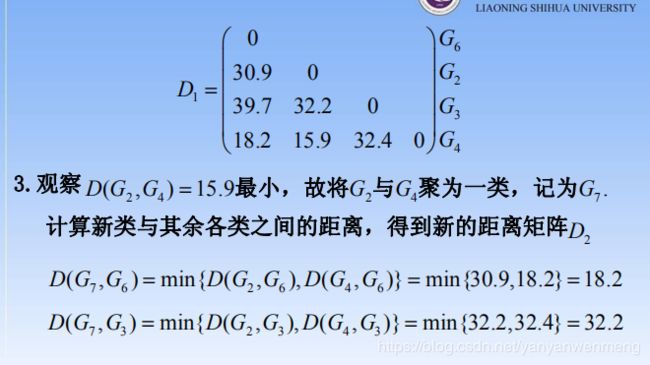
然后是G2和G4聚为一类，命名为G7

计算各类（G6、G7、G3）与新类G7之间的距离，发现G6和G7的距离最短：

然后将G7和G6聚为一类，命名为G8

计算各类（G8和G3）与新类G8之间的距离，发现G3和G8的距离最短：

最后将G3和G8聚为一类，命名为G9 

都聚为1类了，聚类结束。

 

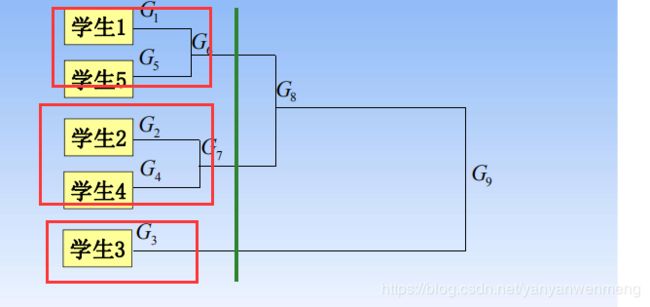
如何进行分类：

 比如我们需要划分为3类，我们画一根绿色的线条，就将学生（样本）划分为了3类。学生1和5为一类，学生2和4为1类，学生3自成一类。

 5.3 最长距离系统聚类法

 

 

 5.4 聚类分析需要注意的问题

1.对于一个实际问题要根据分类的目的来选取指标，指标 选取的不同分类结果一般也不同。

2.样品间距离定义方式的不同，聚类结果一般也不同。

3.聚类方法的不同，聚类结果一般也不同（尤其是样品特别 多的时候）。最好能通过各种方法找出其中的共性。

4.要注意指标的量纲，量纲差别太大会导致聚类结果不合 理。

5.聚类分析的结果可能不令人满意，因为我们所做的是一个 数学的处理，对于结果我们要找到一个合理的解释。

 

6. SPSS操作步骤——系统聚类

 6.1 系统聚类算法流程

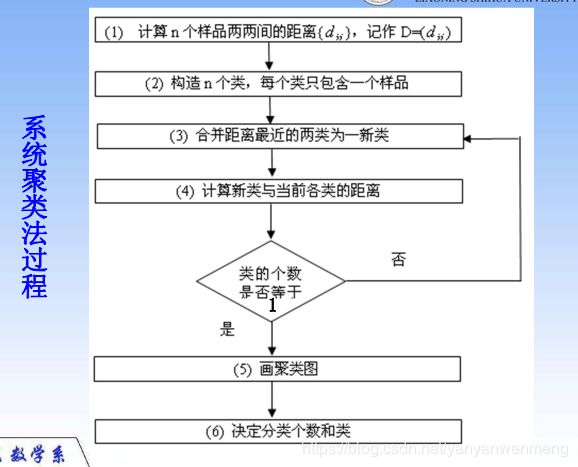
系统（层次）聚类的算法流程：

• 将每个对象看作一类，计算两两之间的最小距离；
• 将距离最小的两个类合并成一个新类；
• 重新计算新类与所有类之间的距离；
• 重复二三两步，直到所有类最后合并成一类；
• 结束。

6.2 SPSS操作步骤

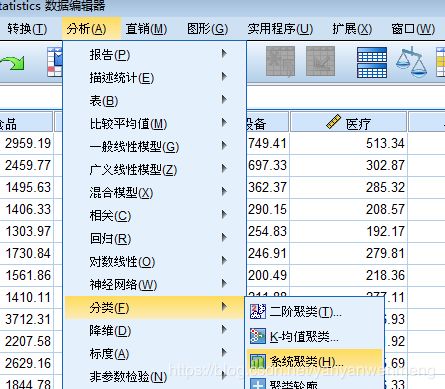
第一步：选择【分析】【分类】【系统聚类】

第二步：将指标放入到【变量】中，将分类依据放入到【个案标注依据】中。

第三步：在【图】中将【谱系图】勾选上。

 

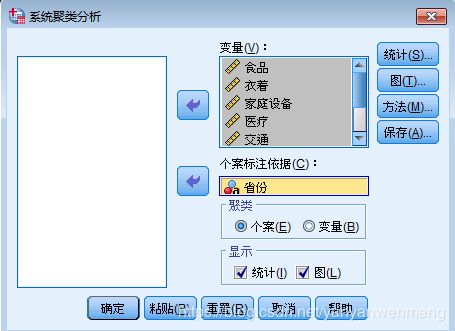
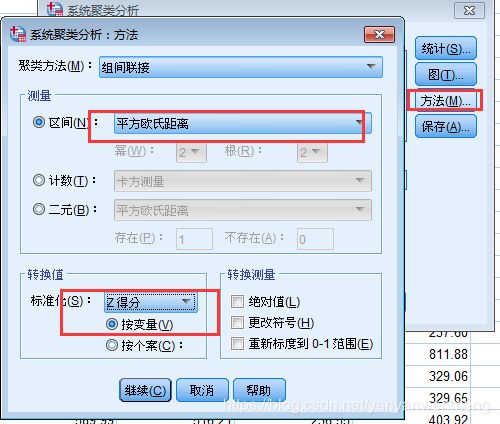
第四步：【方法】中，计算距离时，【区间】可以使用软件默认的【平方欧式距离】，也可以使用欧式距离。如果指标单位不统一，需要对指标进行标准化。一把选择Z标准化【Z得分】。如果单位是统一的就可以不用进行标准化。

 6.3 结果分析

红色的线可以将样本分为2类，绿色的线可以将样本分为3类。

 

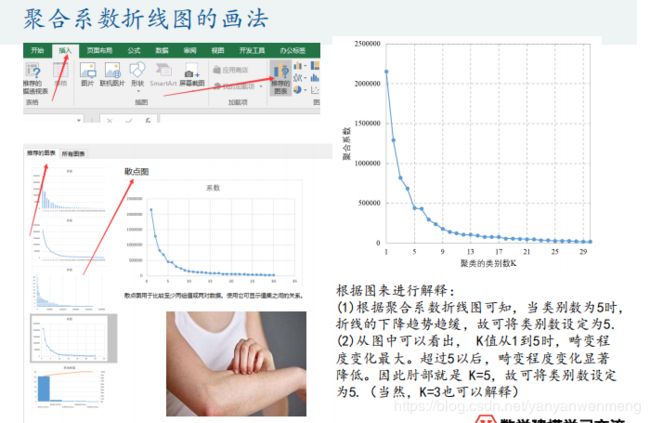
如何选择最佳的K值？

肘部法则：用图形估计聚类的数量。

 

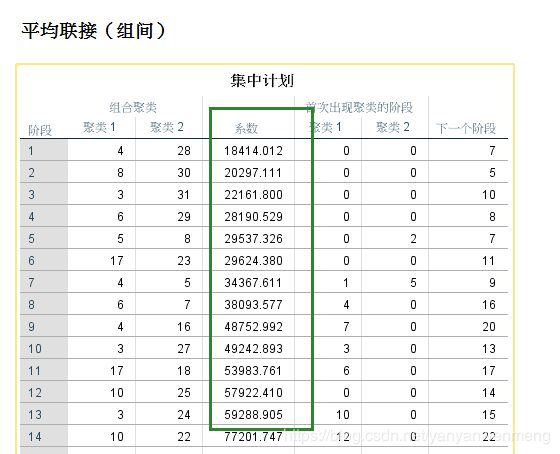
 第一步：将聚合系数（即绿框中的系数）放入到excel表格中。

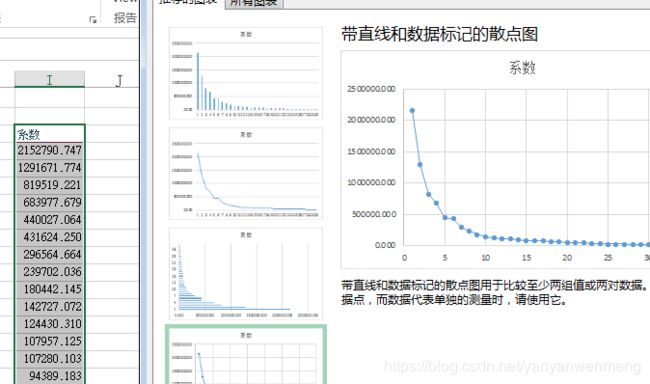
第二步：对聚合系数进行降序排序。

第三步：在插入的图表中选择散点图。

 第四步：对图表进行美化。双击X轴的数据，对其最小值设置为1（最小样本数），最大值设置为30（最大样本数）.因为有1-30个样本。

 第五步：美化后的图表，加上横坐标和纵坐标的描述。

根据图来进行解释：

(1)根据聚合系数折线图可知，当类别数为5时， 折线的下降趋势趋缓，故可将类别数设定为5.

(2)从图中可以看出， K值从1到5时，畸变程 度变化最大。超过5以后，畸变程度变化显著 降低。因此肘部就是 K=5，故可将类别数设定 为5.（当然，K=3也可以解释）