style-GAN:A Style-Based Generator Architecture for Generative Adversarial Networks. (一)
A Style-Based Generator Architecture for Generative Adversarial Networks
author:paper published by NVLab
网站Demon地址:https://thispersondoesnotexist.com/
github地址:http://stylegan.xyz/code
摘要:提出GAN中全新的生成器架构。可以无监督的分割高级属性,生成的图片中也能保持多样性(随机变化),可以直观的、特定尺度的控制合成。新的生成器相比传统生成器,使得拥有更好的插值属性,并且更好的处理隐式变量。(针对新提出的生成器方法,还提出了两种度量方法,目前还不理解)
PS:以下附上了很多引用paper的名字,这些都是目前GAN的重大进展,需要学习。
1, Introduction:
GAN的发展非常迅速,有如下paper[26, 38, 5],有不少令人佩服的结果,是值得阅读的,可以帮助理解GAN的进展:
[26] T. Karras, T. Aila, S. Laine, and J. Lehtinen. Progressive growing of GANs for improved quality, stability, and variation. CoRR, abs/1710.10196, 2017.
[38] T.Miyato, T. Kataoka, M. Koyama, and Y. Yoshida. Spectral normalization for generative adversarial networks. CoRR, abs/1802.05957, 2018.
[5] A. Brock, J. Donahue, and K. Simonyan. Large scale GAN training for high fidelity natural image synthesis. CoRR, abs/1809.11096, 2018.
然而目前这些GAN仍然像个黑盒子,当然也有人致力于解释GAN相关的理论[3] 目前对于图像合成过程的理解仍然欠缺,例如对于初始状态随机特征的理解。隐式空间的属性也很少被理解,目前所述的隐式空间插值[12, 45, 32]并没有提出很权威且普适的衡量方法来和其他GAN对比。
[3] Anonymous. Visualizing and understanding generative adversarial networks. Submitted to ICLR 2019, https://openreview.net/forum?id=Hyg X2C5FX, 2018.
[12]A. Dosovitskiy, J. T. Springenberg, and T. Brox. Learning to generate chairs with convolutional neural networks. CoRR,abs/1411.5928, 2014.
[45] T. Sainburg, M. Thielk, B. Theilman, B. Migliori, and T. Gentner. Generative adversarial interpolative autoencoding: adversarial training on latent space interpolations encourage convex latent distributions. CoRR, abs/1807.06650,2018.
[32] S. Laine. Feature-based metrics for exploring the latent space of generative models. ICLR workshop poster, 2018.
本文的思路最初来源于风格迁移相关paper[23],我们重新设计了生成器架构,某种程度上得到了一个新的方法来控制整个图像合成过程。我们的生成器包括一个输入常量并且在每一个卷积层都基于latent code来调整它的图像风格。每层中都附加入噪声。没有修改判别器和损失函数相关内容。Paper [20, 38, 5, 34, 37, 31]同样值得一读,包含稳定训练GAN的一些方法。
[23] X. Huang and S. J. Belongie. Arbitrary style transfer in real-time with adaptive instance normalization. CoRR,abs/1703.06868, 2017.
提出两种方法:we propose two new automated metrics—perceptual path length and linear separability—for quantifying these aspects of the generator.(目前还不理解)
提出一个新的人脸数据集:(Flickr-Faces-HQ, FFHQ)
2. Style-based generator

左图a)是传统的GAN,右图b)是paper提出的改进的新结构。其主要特点如下:
- 输入是常量即Const 4x4x512。
- Latent Z经过8层MLP转换为W,维度为每层神经元个数有512个。
- 每层网络都加入了style和Noise,style经由Latent Z ==> W,再由W经过仿射变换得到。最后style和Noise经过AdaIN的norm处理。
- 全部生成器层数18层
- Here “A” stands for a learned affine transform(仿射变换), and “B” applies learned per-channel scaling factors to the noise input.(没懂)
- 最后一层是decode层,将图片转为RGB(使用1 x 1卷积层)
2.1 Quality of generated images
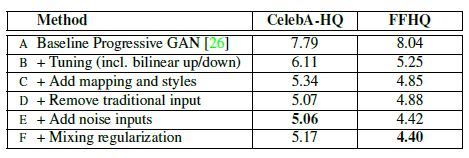
可以看到在基础模型上一步一步做改变可以证明该架构的有效性。
最初是用Baseline在两个数据集上跑,得到FID(越小越好),先通过Tuning,再加入mapping和style部分,再去除传统输入层,再加上噪声输入,最后加上Mixing regularization得到最好的FID,每一步都可以优化,这也是为什么说style-GAN是GAN2.0。以后这种结构将被大量的研究借鉴。
2.2. Prior art
目前一些相关技术:
- 很多GAN着重判别器的优化,如:使用多个判别器[15, 40],使用多尺度(不清楚多尺度的含义)判别器[52,48],或者使用self-attention[55]。
- 在判别器方面的工作大多数focus在输入空间的精确分布上[5]或者通过高斯混合模型shaping一下[4]、还有聚类[41]、或者鼓励凸性(encouraging convexity [45].)
- 最近的工作中有给每层生成器feed对应的类标签,该类标签有单独的embedding网络[39],然而其输入仍然是传统的输入方式。
- 一些作者考虑将部分latent code feed到多个生成器的层中去[9,5],具体细节以及与本文的区别没多提。
- 与本文类似的工作有Chen et al.[6]“self modulate”使用了AdaINs方法,但没考虑隐式空间和噪声的输入。
[15] I. P. Durugkar, I. Gemp, and S. Mahadevan. Generative multi-adversarial networks. CoRR, abs/1611.01673, 2016.
[40] G. Mordido, H. Yang, and C. Meinel. Dropout-gan: Learning from a dynamic ensemble of discriminators. CoRR, abs/1807.11346, 2018.
[52] T. Wang, M. Liu, J. Zhu, A. Tao, J. Kautz, and B. Catanzaro. High-resolution image synthesis and semantic manipulation with conditional GANs. CoRR, abs/1711.11585, 2017.
[48] R. Sharma, S. Barratt, S. Ermon, and V. Pande. Improved training with curriculum gans. CoRR, abs/1807.09295, 2018.
[55] H. Zhang, I. Goodfellow, D. Metaxas, and A. Odena. Self-attention generative adversarial networks. CoRR, abs/1805.08318, 2018.
[5] A. Brock, J. Donahue, and K. Simonyan. Large scale GAN training for high fidelity natural image synthesis. CoRR, abs/1809.11096, 2018.
[4] M. Ben-Yosef and D. Weinshall. Gaussian mixture generative adversarial networks for diverse datasets, and the unsupervised clustering of images. CoRR, abs/1808.10356, 2018.
[41] S. Mukherjee, H. Asnani, E. Lin, and S. Kannan. Cluster-GAN : Latent space clustering in generative adversarial networks. CoRR, abs/1809.03627, 2018.
[45] T. Sainburg, M. Thielk, B. Theilman, B. Migliori, and T. Gentner. Generative adversarial interpolative autoencoding: adversarial training on latent space interpolations encourage convex latent distributions. CoRR, abs/1807.06650,2018.
[39] T. Miyato and M. Koyama. cGANs with projection discriminator. CoRR, abs/1802.05637, 2018.
[9] E. L. Denton, S. Chintala, A. Szlam, and R. Fergus. Deep generative image models using a Laplacian pyramid of adversarial networks. CoRR, abs/1506.05751, 2015.
[6] T. Chen, M. Lucic, N. Houlsby, and S. Gelly. On self modulation for generative adversarial networks. CoRR, abs/1810.01365, 2018.
3. Properties of the style-based generator
…
未完待续…