SAGPool - Self-Attention Graph Pooling 图分类 图池化方法 ICML 2019

论文：Self-Attention Graph Pooling

作者：Junhyun Lee, Inyeop Lee, Jaewoo Kang
韩国首尔高丽大学计算机科学与工程系

来源：ICML 2019

论文链接：
Arxiv: https://arxiv.org/abs/1904.08082

github链接：https://github.com/inyeoplee77/SAGPool

近年来，人们提出了将深度学习应用于图数据等结构化数据的方法。研究工作集中在将CNN泛化到图数据，重新定义图数据的卷积操作和downsampling(池化)操作。将卷积运算推广到图上的方法已被证明了可以提高性能，并得到了广泛的应用。然而，将downsampling应用于图数据的方法仍然难以实现，还有改进的空间。此文提出了一种基于self-attention的图池化方法。使用图卷积的self-attention使得化池化方法同时考虑了节点特征和图的拓扑结构。实验中，为了确保公平的比较，将现有的池化方法和文中提出的SAGPool方法使用了相同的训练流程和模型架构。实验结果表明，该方法使用合理数量的参数，在基准数据集上获得了较好的图分类性能。

1 相关介绍

背景

目前，图池化的方法比图卷积的方法要少，而现存的基于池化的方法存在一些问题：

• 以往的基于拓扑的池化的研究都只考虑了图的拓扑结构。
• 而全局池化方法只考虑了图的特征。
• 分层池化可以学到图的层次表示（DIFFPOOL），允许图神经网络(GNNs)以端到端方式汇聚后获得按比例缩小的图，但是具有二次方的空间复杂度，其参数数量取决于节点数量。分层池化gPool解决了复杂度问题，但没有考虑图的拓扑结构。

创新性

文中提出了SAGPool，这是一种基于层次图池化的Self-Attention Graph方法。

• SAGPool方法可以使用相对较少的参数以端到端方式学习分层表示。
• 利用self-attention机制来区分应该删除的节点和应该保留的节点。
• 基于图卷积计算注意力分数的self-attention机制，考虑了节点特征和图的拓扑结构。

简而言之，SAGPool具有前几种方法的优点：分层池化，同时考虑节点特征和图的拓扑结构，合理的复杂度，以及端到端表示学习。SAGPool是第一个使用self-attention进行图池化处理并实现高性能的方法。SAGPool参数量一致，不用考虑输入图的大小。

2 相关工作

GNNs因其在图领域中的表现而备受关注。CNN模型中的池化层通过缩小图片的表示的大小来减少参数的数量，从而避免过拟合问题。为了将CNNs推广到图数据上，GNNs使用池化方法是必要的。图数据池化方法可以分为以下三类:基于拓扑的池化、全局池化和分层池化。

基于拓扑的池化

早期的工作使用的是图的粗化算法，而不是使用神经网络。谱聚类算法利用特征分解得到粗化图。然而，由于特征分解的时间复杂度过大问题，需要一些替代方法：
（1） Weighted graph cuts without eigenvectors a multilevel approach, 2007
Graclus计算了给定图无特征向量的的聚类，因为一般谱聚类目标和加权核k-means目标之间存在数学等价性。
（2）在最近的GNN模型中Graclus被用作池化模块：

• Convolutional neural networks on graphs with fast localized spectral filtering，NIPS 2016
• Hybrid approach of relation network and localized graph convolutional filtering for breast cancer subtype classification，IJCAI 2018

全局池化

与基于拓扑的池化方法不同，全局池化方法考虑了图的特征。全局池化方法使用求和或神经网络pool每个层中所有节点的表示。全局池化方法pool所有的表示，可以处理具有不同结构的图：
（1）Neural message passing for quantum chemistry，2017)
将GNNs视为消息传递方案，提出了一种图分类的通用框架，利用Set2Set方法可以获得整个图的表示。
（2）An end-to-end deep learning architecture for graph classification，AAAI 2018
SortPool:根据图的结构对节点的embeddings进行排序，并将排序后的embeddings传递给下一层。

分层池化

全局池化方法没有学习对捕获图结构信息至关重要的层次表示。分层池化方法的主要动机是建立一个能够学习每一层中基于特征或拓扑的节点assignment的模型：
（1）[DIFFPOOL] Hierarchical Graph Representation Learning with Differentiable Pooling，NeurIPS 2018
DIFFPOOL是一种可微的图池化方法，能够以端到端的方式学习assignment矩阵：$S^{(l)}\in {\mathbb{R}}^{n_l\times n_{l+1}}$，$n_l$表示在第$l$层的节点数，$n_{l+1}$表示在第$l+1$层的节点数，$n_l<n_{l+1}$，即行数等于第$l$层的节点数（cluster数），列数代表第$l+1$层的节点数（cluster数）。assignment matrix表示第$l$层的每一个节点到第$l+1$层的每一个节点（或cluster）的概率。

具体而言，节点根据下面的公式分到下一层的cluster：

$$S^{(l)}=\mathrm{softmax}\left({\mathrm{G}\mathrm{N}\mathrm{N}}_l\left(A^{(l)},X^{(l)}\right)\right)$$

$$A^{(l+1)}=S^{(l)\top }{A}^{(l)}{S}^{(l)}\text{\hspace{1em}(1)}$$
具体细节，可以参考另一篇博文：[DIFFPOOL 图分类] - Hierarchical Graph Representation Learning with Differentiable Pooling NeurIPS 2018

（2）Graph u-net，ICML 2019
gPool实现了与DiffPool相当的性能。gPool需要$O(|V|+|E|)$的空间复杂度，而DiffPool需要$O(k|V{|}^2)$，其中$V,E,k$分别表示顶点数、边数和池化比率。gPool使用一个可学习的向量$p$来计算投影分数，然后使用这些分数来从图中选择排名最高的节点保留下来。投影分数由$p$与各节点特征的点积得到。分数表示可以保留的节点信息量。下式大致描述了gPool中的池化过程：

$$y=X^{(l)}{\mathbf{p}}^{(l)}/\Vert {\mathbf{p}}^{(l)}\Vert ,\text{ id }\mathbf{x}=\mathrm{top}-\mathrm{rank}(y,\lceil kN\rceil )$$

$$A^{(l+1)}=A_{\mathrm{i}\mathrm{d}\mathrm{x},\mathrm{i}\mathrm{d}\mathrm{x}}^{(l)}\text{\hspace{1em}(2)}$$
在公式（2）中，投影分数的计算没有考虑图的拓扑结构。

为了进一步改进图池化方法，文中提出了SAGPool，它可以使用图的特征和拓扑结构信息来产生具有合理的时间和空间复杂度的层次表示。

3 方法

SAGPool的关键在于它使用GNN来提供self-attention分数。

3.1 基于self-attention的图池化方法：SAGPool

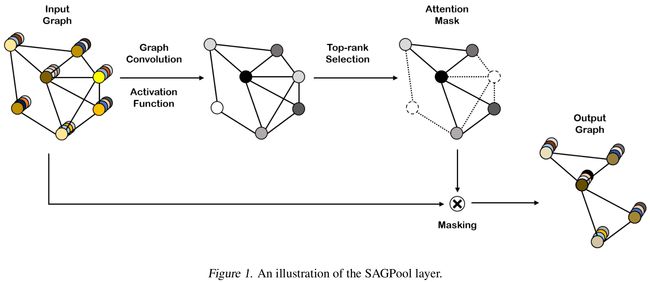
• 图1是SAGPool层的结构图

Self-attention mask

注意力机制在最近的深度学习研究中被广泛应用。这种机制可以使我们能够关注更重要的特征。self-attention，通常被称为intra-attention，关注的特征是注意力本身。SAGPool利用图卷积的方法得到self-attention分数。例如，如果使用Kipf的图卷积公式，则self-attention分数$Z\in {\mathbb{R}}^{N\times 1}$根据如下计算：

$$Z=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}X{\Theta }_{att}\right)\text{\hspace{1em}(3)}$$

• ${\Theta }_{att}\in {\mathbb{R}}^{F\times 1}$是SAGPool层中的唯一参数
• 其他符号表示和GCN中相同

因为利用图卷积得到self-attention分数，所以这种池化的结果是基于图的特征和拓扑的。

SAGPool采用了gPool中的节点选择方法，保留了输入图的一部分节点：

$$\mathrm{i}\mathrm{d}\mathrm{x}=\mathrm{t}\mathrm{o}\mathrm{p}-\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}(Z,\lceil kN\rceil ),Z_{mask}=Z_{\mathrm{i}\mathrm{d}\mathrm{x}}\text{\hspace{1em}(4)}$$

• 池化比率$k\in (0,1]$是一个超参数，它决定要保留的节点数
• top$\lceil kN\rceil$的节点是根据$Z$的值来选择的
• $\mathrm{t}\mathrm{o}\mathrm{p}-\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}$是返回top$\lceil kN\rceil$的节点的索引的函数
• ${.}_{idx}$是一个索引操作
• $Z_{mask}$是feature attention mask

图池化

输入图由图1中标记为masking的操作处理。

$$X^{\prime }=X_{\mathrm{i}\mathrm{d}\mathrm{x},:},X_{out}=X^{\prime }\odot Z_{mask},A_{out}=A_{\mathrm{i}\mathrm{d}\mathrm{x},\mathrm{i}\mathrm{d}\mathrm{x}}\text{\hspace{1em}(5)}$$

• $X_{\mathrm{i}\mathrm{d}\mathrm{x},:}$是索引按行排列的特征矩阵 (每一行代表一个节点的特征向量)
• $X_{out}$是新的特征矩阵
• $A_{out}$是新的邻接矩阵
• $A_{\mathrm{i}\mathrm{d}\mathrm{x},\mathrm{i}\mathrm{d}\mathrm{x}}$是按行和按列索引的邻接矩阵

SAGPool的变种

SAGPool中使用图卷积的主要原因是为了获得拓扑结构和节点特征。如果GNNs以节点特征和邻接矩阵为输入，则可以用式(3)Kipf的图卷积公式代替GNNs的各种公式。计算注意力分数$Z\in {\mathbb{R}}^{N\times 1}$的广义公式如下:

$$Z=\sigma (\mathrm{GNN}(X,A))\text{\hspace{1em}(6)}$$

计算注意力分数，不仅可以使用相邻节点，也可以使用多跳连接的节点。可以使用添加改变邻接矩阵形式扩展边，堆叠多层GNN层，使用多个注意力分数的平均值等方法来达到这个目的。

以一个连接两跳的节点为例。
（1）添加邻接矩阵的平方：${\text{ SAGPool}}_{\text{augmentation}}$
式(7)使用了两跳连接，该连接涉及边的扩展，允许两跳节点的间接聚合。添加邻接矩阵的平方相当于在两跳邻居之间创建了边：

$$Z=\sigma \left(\mathrm{GNN}\left(X,A+A^2\right)\right)\text{\hspace{1em}(7)}$$

（2）叠加两层GNN层：${\text{ SAGPool}}_{\text{serial}}$
式(8)使用了两跳连接，该连接涉及GNN层的堆叠，允许两跳节点的间接聚合。在这种情况下，SAGPool层的非线性和参数数量将增加：

$$Z=\sigma \left({\mathrm{GNN}}_2\left(\sigma \left({\mathrm{GNN}}_1(X,A)\right),A\right)\right)\text{\hspace{1em}(8)}$$
公式（7）和公式（8）可以应用到更多跳的连接上。

（3）取多个注意力分数的平均值：${\text{ SAGPool}}_{\text{parallel}}$
另一种方法取多个注意力得分的平均值。$M$个GNNs平均注意力分值如下:

$$Z=\frac{1}{M}\sum _m\sigma \left({\mathrm{G}\mathrm{N}\mathrm{N}}_m(X,A)\right)\text{\hspace{1em}(9)}$$

文中分别将公式（7），（8），（9）中的模型称为${\text{ SAGPool}}_{\text{augmentation}}$，${\text{ SAGPool}}_{\text{serial}}$和${\text{ SAGPool}}_{\text{parallel}}$。

3.2 模型架构

• 图2左图是全局池化结构，右图是分层池化结构
• 全局池化结构由三个图卷积层组成，每层的输出被连接起来。节点特征在池化层之后的readout层中聚合。然后将图的特征表示传递到线性层进行分类。
• 分层池化架构由三个block组成，每个block由一个图卷积层和一个图池化层组成。每个block的输出汇总在readout层中。将每个readout层输出的总和输入到线性层进行分类。
• 这些架构应用于所有baseline和SAGPool，以便进行公平的比较。
• 在文中，左边使用了POOL方法（如${\text{SAGPool}}_g$,${\text{gPool}}_h$）的架构称为${\text{POOL}}_g$，右边的称为${\text{POOL}}_h$。

根据（Troubling trends in machine learning scholarship，2018）的观点，如果对一个模型进行了多次修改，那么就很难确定哪些修改有助于提高性能。为了公平的比较，文中采用了SortPool（AAAI 2018）和（Towards sparse hierarchical graph classifiers，2018）中的模型架构，并使用相同的架构来比较baseline和文中的方法。

卷积层

使用Kipf的GCN：
$$h^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{h}^{(l)}\Theta \right)\text{\hspace{1em}(10)}$$

• $\Theta \in {\mathbb{R}}^{F\times F^{\prime }}$
• $F$和$F^{\prime }$分别表示第$l+1$层的输入特征维度和输出特征维度
• 激活函数使用ReLU

readout层

受JK-net架构（Representation learning on graphs with jumping knowledge networks，2018；Towards sparse hierarchical graph classifiers，2018）的启发，提出了一种readout层，该层聚合节点特征以形成固定大小的表示。readout层的输出特征如下:

$$s=\frac{1}{N}\sum _{i=1}^N{x}_i\Vert \underset{i=1}{\overset{N}{\max }}{x}_i\text{\hspace{1em}(11)}$$

• $N$表示节点数量
• $x_i$表示第$i$个节点的特征
• $||$，表示concatenation，即特征串联操作

全局池化架构

实现了（An end-to-end deep learning architecture for graph classification，AAAI 2018）中提出的全局池化架构。

分层池化架构

实现了（Towards sparse hierarchical graph classifiers，2018）分层池化架构。

4 实验

在图分类任务中，评估了全局池化和分层池化方法。

数据集

选取了5个图的数量较大的数据集（$>1k$）:

• D&D
  包含蛋白质结构的图。一个节点表示一个氨基酸，如果两个节点之间的距离小于$6\hat{\mathrm{A}}$，则构造一挑边。标签表示蛋白质是酶还是非酶。
• PROTEINS
• 也是一组蛋白质，其中节点是二级结构元素。如果节点具有边，则节点处于氨基酸序列中或在封闭的三维空间中。
• NCI1
  是一个用于抗癌活性分类的生物数据集。在数据集中，每个图表示一个化合物，节点和边分别表示原子和化学键。
• NCI109
• FRANKENSTEIN
  是一组具有包含连续值的节点特征的分子图。标签表示一个分子是诱变剂还是非诱变剂。

GNNs的评估

• 所有模型均采用相同的early stopping准则和超参数选择策略，以保证比较的公平性。
• 使用NVIDIA TitanXp GPU
• 使用几何深度学习扩展库PyG实现所有的baselines和SAGPool

训练过程

• （Pitfalls of graph neural network evaluation，2018）证明了不同的数据分割会影响GNN模型的性能。
• 在实验中，使用10-fold交叉验证评估了超过20个随机种子的池化方法。
• 总共使用了200个测试结果来获取每个数据集上每个方法的最终精度。
• 使用训练集的10%的数据进行验证。
• 使用了Adam优化器、early stopping准则、patience以及全局池化结构和分层池化结构的超参数选择策略。如果在epoch终止条件下最多100k个epoch验证损失没有改善，将停止训练。
• 通过网格搜索得到最优超参数。网格搜索的范围如表2所示。

Baselines

• Set2Set
  Set2Set需要额外的超参数，即LSTM模块的处理step数。LSTM模块为节点顺序不变的图生成embedding，所以可以假设readout层是不必要的。
• SortPool
  SortPool是一种全局池化方法，它对节点进行排序来进行池化。节点数量设置为$K$，使得图的60%有多于$K$个的节点。在全局池化设置中，${\text{ SAGPool }}_g$与SortPool具有相同的$K$个输出节点。
• DiffPool
  DiffPool是第一种端到端可训练的图池化方法，它可以生成图的分层表示。使用中没有对DiffPool使用batch normalization，因为这与池化方法无关。对于超参数搜索，池化比率从0.25到0.5不等。在引用的实现中，cluster大小设置为节点的最大数目的25%。当池化比率大于0.5时，DiffPoolh会导致内存不足。
• gPool
  gPool为池化选择排名靠前的节点，与SAGPool方法类似。通过与gPool的比较表明，考虑拓扑结构有助于提高图形分类任务的性能。

DiffPool,gPool和${\text{ SAGPool }}_h$使用分层池化架构；
Set2Set, SortPool和${\text{ SAGPool }}_g$使用全局池化架构；
对所有的baselines和SAGPool使用相同的超参数搜索策略。超参数如表2所示。

SAGPool的变种

• SAGPool的三个变体用于获得注意力得分$Z$
• ${\text{ SAGPool }}_{augmentation}$使用公式（7）
• ${\text{ SAGPool }}_{serial}$使用公式（8）
• ${\text{ SAGPool }}_{paralle}$使用多个GNN计算注意得分，对得分求平均以获得最终注意得分
• 使用方程（9）评估M=2和M=4的性能

$$Z=\frac{1}{M}\sum _m\sigma \left({\mathrm{G}\mathrm{N}\mathrm{N}}_m(X,A)\right)\text{\hspace{1em}(9)}$$

结果总结

5 分析

全局池化和分层池化

• 很难确定全局池化结构或层次池化结构是否完全有利于图形分类。
• 因为全局池化结构$POO{L}_g$（${\text{ SAGPool }}_g$、${\text{ SortPool }}_g$、${\text{ Set2Set }}_g$）使信息丢失最小化，因此它在节点较少的数据集（NCI1、NCI109、FRANKENSTEIN）上的性能优于分层池化结构$POO{L}_h$（${\text{ SAGPool }}_h$、${\text{ gPool }}_h$、${\text{ DiffPool }}_h$）。
• 然而，分层池化$POO{L}_h$对节点数较多的数据集（D&D和PROTEINS）更有效，因为它能有效地从大规模图中提取有用的信息。
• 因此，使用最适合给定数据的池化结构非常重要。
• 尽管如此，SAGPool在每种架构中通常都表现良好。

考虑图拓扑结构的影响

• 为了计算节点的注意力分数,${\text{ SAGPool }}_h$利用公式(3)所示的图卷积。
• 和gPool不一样, SAGPool使用一阶近似图的拉普拉斯算子${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$，这使得SAGPool考虑了图的拓扑结构。如表3所示，考虑图的拓扑结构可以提高性能。此外，图的Laplacian算子不需要重新计算，因为它在前一个图卷积层中也使用了，可以预先计算。
• 虽然SAGPool具有与gPool相同的参数，但它在图分类任务中表现出了更优异的性能。

• 结果表明，SAGPool在总体上表现良好，在D&D和PROTEINS方面表现尤为突出。
• 在实验中，SAGPool在所有的数据集上都优于分层池化的方法。
• SAGPool变体的实验结果表明，SAGPool具有提高性能的潜力。

稀疏实现

• 使用稀疏矩阵操作图数据对于GNNs来说非常重要，因为邻接矩阵通常是稀疏的。
• 用稠密矩阵计算图卷积时，乘法$AX$的计算复杂度为$O(|V{|}^2)$，其中$A$为邻接矩阵，$X$为节点特征矩阵，$V$为顶点。
• 如(Towards sparse hierarchical graph classifiers，2018)所述，密集矩阵池化会导致内存效率问题。
• 如果在同一操作中使用稀疏矩阵，则计算复杂度降低到$O(|E|)$，其中$E$表示边。由于SAGPool是一种稀疏池化方法，使用稀疏实现可以降低计算复杂度，而DiffPool是一种密集池化方法，计算复杂度较高。
• 稀疏性也影响空间复杂性。因为SAGPool使用GNN来获取注意力分数，所以SAGPool需要$O(|V|+|E|)$的稀疏池化存储空间，而稠密池化方法需要$O(|V{|}^2)$。

节点数量的关系

在DiffPool中，由于GNN产生了如式(1)所示的assignment矩阵S，因此在构建模型时必须定义cluster的大小。根据参考方法的实现，cluster的大小必须与最大节点数成比例。DiffPool的这些要求会导致两个问题。

• 参数的数量取决于最大节点数，如图3所示。
• 当节点数量变化很大时，很难确定正确的cluster大小。例如，在1178个图中只有10个图具有超过1000个节点，其中最大节点数为5748，最小节点数为30。如果池化比率为10%，则cluster大小为574，这将扩展大多数数据池化后的图大小。

在SAGPool中，参数的数量与cluster的大小无关。此外，可以根据输入节点的数量更改cluster大小。

• 图3：图中参数的数量随着节点的增多而增大。
• x轴标号为输入图节点数
• y轴为分层池化模型参数:输入节点特征数为128，隐含层特征大小为128，class数为2。
• SAGPool使用公式（3）的图卷积。
• $k$表示池化比率，$k=1.0$表示池化后保留整个节点。
• 无论输入图的大小和池化比率如何，gPool和SAGPool参数数量都一致。

SAGPool变种比较

为了研究SAGPool方法的潜力，在两个数据集上评估了SAGPool的变种。可以用以下操作修改SAGPool:

• 更改GNN的类型
• 考虑两跳连接。实验中使用两个连续GNN层（${\text{ SAGPool }}_{serial}$）和添加邻接矩阵的方式来实现2跳连接（${\text{ SAGPool }}_{augmentation}$）。
• 对多个GNN的注意力得分求平均值

• 使用的数据集和SAGPool中的GNN类型不同，图分类的性能有所不同
• 两跳邻居的信息有助于提高性能
• 发现为数据集选择合适的$M$值有助于实现稳定的性能

当前方法的局限性

• 保留一定比例(池化比率$k$)的节点来处理不同大小的不同输入图，这在之前的研究中也做过
• 在SAGPool中，无法为每个图将池化比率参数化来找到最优值。为了解决这个问题，文中使用二分类来决定保留哪些节点，但是这并没有完全解决问题。

可能的扩展工作

• 为每个图使用可学习的池化比率来获得最优的cluster大小
• 研究每个池化层中多attention mask的影响