HAN - Heterogeneous Graph Attention Network 异构图注意力网络 WWW 2019

论文题目：Heterogeneous Graph Attention Network (HAN) 异构图（异质图）注意力网络

作者：北京邮电大学的Xiao Wang, Houye Ji等人

来源：WWW 2019

论文链接：https://arxiv.org/pdf/1903.07293.pdf

tensorflow版代码Github链接：https://github.com/Jhy1993/HAN

介绍视频：https://www.bilibili.com/video/av53418944/

文中提出了一种新的基于注意力机制的异质图神经网络 Heterogeneous Graph Attention Network（HAN），可以广泛地应用于异质图分析。注意力机制包括节点级注意力和语义级注意力。节点的注意力主要学习节点及其邻居节点间的权重，语义级的注意力是来学习基于不同meta-path的权重。最后，通过相应地聚合操作得到最终的节点表示。

1 相关介绍

背景

以 Graph Convolutional Network，Graph Attention Network 为代表的图神经网络已经引起了学术界与工业界的广泛关注。然而，目前的图神经网络主要针对同质图（节点类型和边类型单一）设计，但真实世界中的图大部分都可以很自然地建模为异质图（多种类型的节点和边）。如图 1 所示，IMDB 数据中包含三种类型的节点 Actor、Movie 和 Director，两种类型的边 Actor-Movie 和 Movie-Director。

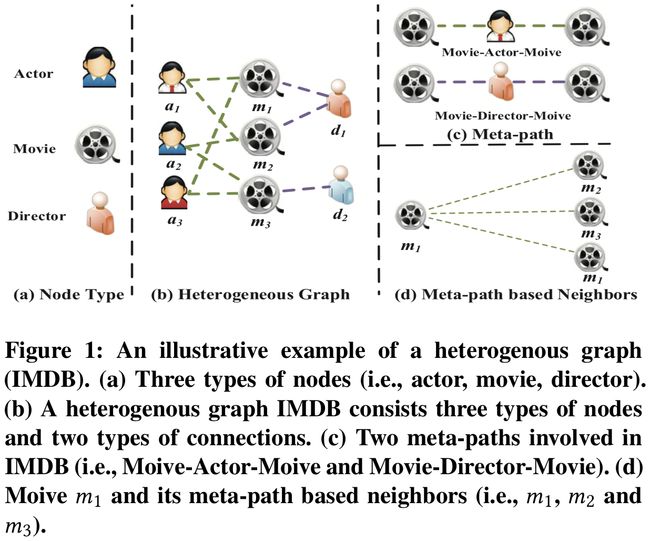
相对于同质图神经网络，异质图神经网络具有更强的现实意义可以更好的满足工业界需求。如阿里巴巴正在建设亿级节点十亿级边的异质图神经网络平台 AliGraph 来满足整个阿里集团各种商业化场景需求。因此亟需展开面向异质图的图神经网络模型研究，而异质图的异质性却又给设计图神经网络带来了巨大的挑战。

元路径 meta-path

在异构图中，两个节点可以通过不同的语义路径连接，称为元路径（meta-path），如图1中，Movie-Actor-Movie（MAM）和Movie-Year-Movie (MYM)都是不同的meta-path。不同的meta-path有不同的语义。如图1中， meta-path Movie-Actor-Movie (MAM)表示电影的演员相同， meta-path Movie-Director-Movie (MDM) 表示电影的导演相同。

数学定义：一个meta-path$\Phi$定义为一条由$A_1\stackrel{R_1}{⟶}{A}_2\stackrel{R_2}{⟶}\dots \stackrel{R_l}{⟶}{A}_{l+1}$组成的路径(可以缩写成$A_1{A}_2\cdots A_{l+1}$)。$R=R_1\circ R_2\circ \cdots \circ R_l$定义为对象$A_1$和$A_{l+1}$之间的复合关系。$\circ$表示在关系上的复合操作。

基于meta-path的邻居${\mathcal{N}}_i^{\Phi }$：给定一个节点$i$和一条meta-path $\Phi$，节点$i$的基于meta-path的邻居${\mathcal{N}}_i^{\Phi }$定义为通过meta-path$\Phi$和节点$i$相连的节点构成的集合，包括节点$i$自身。

异构图和同构图

• Heterogeneous Graph（异构图）：异构图是一种特殊的异构信息网络，包含了多种类型的边和节点。例如，图1中的演员节点的特征可能包括性别，年龄和国籍，而电影节点的特征可能包括情节，演员等。边的不同类型可以体现在电影与导演的拍摄关系演员与电影的角色扮演关系。
• Homogeneous Graph（同构图）：同构图的节点类型和边的类型单一。例如，引文网络中的节点都是文档。

在设计异质图神经网络的时候，从异质图的复杂结构出发，需要满足下面三个要求：

• 图的异质性：考虑不同节点和不同关系的差异。不同类型节点有其各自的特征，节点的特征空间也不尽相同。如何处理不同类型的节点并同时保留各自的特征是设计异质图神经网络时迫切需要解决的问题；
• 语义级别注意力：学习meta-path的重要性并融合语义信息。异构图涉及到不同的有意义和复杂的语义信息，这些信息通常由meta-path来反映，对于某个具体任务，不同meta-path表达的语义不同，因此对任务的贡献也不同。例如，以IMDB数据集为例，电影《终结者》要么通过Movie-Actor-Movie（MAM）的方式与《终结者2》连接（主演相同），要么通过Movie-Year-Movie (MYM) 的方式与《Irdyvia》连接（均于1984年拍摄）。在确定了电影《终结者》的类型时，连接方式MAM比MYM更有意义。平等地对待不同的meta-path是不现实的，它会削弱一些有用的meta-path所提供的信息。因此，如何设计针对meta-path的注意力机制是异质图神经网络中的一个基本问题；
• 节点级别注意力：学习基于meta-path的节点邻居的重要性。在异构图中，节点可以通过各种类型的关系（如meta-path）连接。给定meta-path，每个节点都有很多基于meta-path的邻居。如何区分邻居间的细微差别，选择一些信息量大的邻居是有必要的。对于每个节点，节点级注意力的目的是学习基于meta-path的邻居的重要性，并为它们分配不同的注意力值。仍然以IMDB为例，当使用meta-path为 Movie-Director-Moive，终结者将连接到《终结者2》（二者导演相同）。为了更好地确定《终结者》科幻电影的类型，模型应该更多地关注《终结者2》，而不是《泰坦尼克号》，因此，如何设计一个模型来发现邻居们之间的细微差别并正确地学习他们的权重将是一个值得研究的问题。

相关工作

Graph Neural Network

GNN作为深度学习领域的扩展，用来处理无规则图结构数据。GCN可以分为两类，分别是谱域和非谱域。谱方法用于谱表示的图中，非谱域方法直接在图上进行卷积，对空间上的近邻进行操作。

注意力机制在深度学习中有广泛的应用，self-attention、soft-attention等。也已经有很多基于图Attention的应用，上述图神经网络不能处理各种类型的节点和边，只能应用于同构图。

Network Embedding

网络嵌入或者网络表示学习，是在保留网络结构及其属性的前提下，将网络转换到低维空间以应用。以往的方法有很多，随机游走、 深度神经网络、矩阵分解和其他方法，如LINE，也都是基于同构图的。

贡献

• 第一次基于注意力机制的异构图神经网络研究。
• 提出了一种新的基于注意力机制的异质图神经网络 Heterogeneous Graph Attention Network（HAN），可以广泛地应用于异质图分析。HAN模型是高效的，相对于meta-path节点对的数目具有线性复杂度，可以应用于大规模异构图。
• 进行了广泛的实验，以评估HAN模型的性能。结果表明，该模型与现有模型相比具有优越性。通过分析这种分层的注意力机制，证明了HAN对异质图分析具有潜在地良好的解释能力。

2 HAN模型

HAN模型遵循一个层次注意力结构：节点级注意力→语义级注意力。图2展示了汉语言的整个框架。首先，我们提出阳极级注意来学习基于元路径的邻域的权值，并对其进行聚合得到语义特定的节点嵌入，然后，HAN通过语义级注意来区分元路径的不同，从而得到特定任务的语义特定的节点嵌入的最优加权组合。

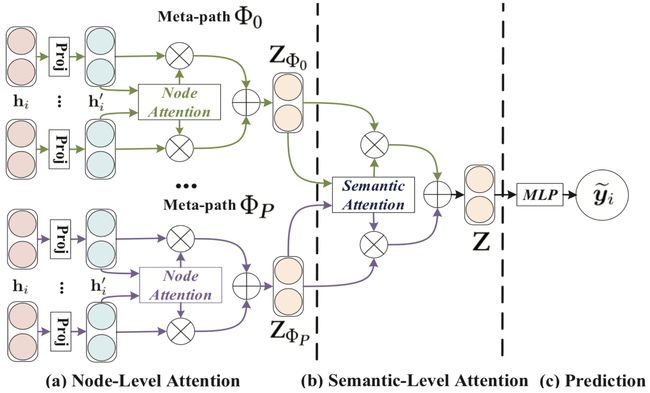
• 图2是HAN整个框架的示意图
• 图2-a（节点级注意力）：所有类型的节点都被投影到一个统一的特征空间中，通过节点级的注意力机制来学习基于meta-path的邻居节点的权重并将它们进行聚合得到特定语义的节点embedding。
• 图2-b（语义级注意力）：联合学习每个meta-path的权重，并通过语义级注意力融合前面得到的语义特定的节点embedding。
• 图2-c ：计算损失和对提出的HAN进行端到端的优化。

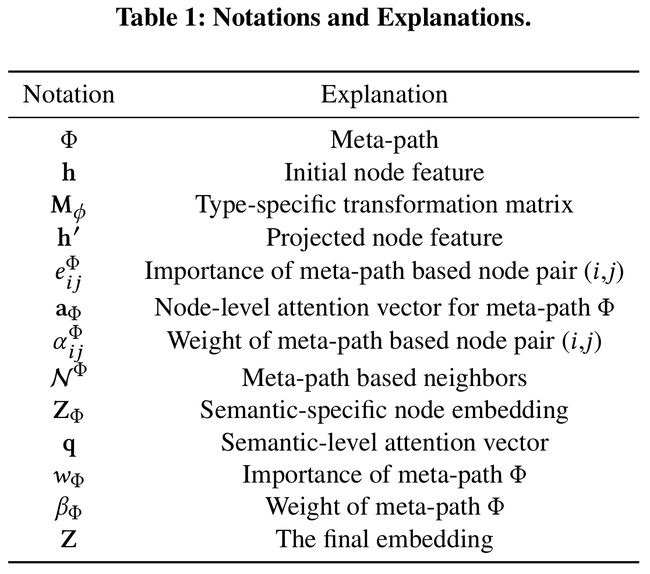
2.1 Node-level Attention

给定某条meta-path，可以利用节点级注意力来学习特定语义下的节点表示。文中应用一个特定类型的转换矩阵${\mathbf{M}}_{{\varphi }_i}$将节点的不同类型的特征通过投影变换到统一的特征空间：

$${\mathbf{h}}_i^{\prime }={\mathbf{M}}_{{\varphi }_i}\cdot {\mathbf{h}}_i\text{\hspace{1em}(1)}$$

• ${\varphi }_i$表示不同类型
• ${\mathbf{h}}_i$和${\mathbf{h}}_i^{\prime }$分别表示节点$i$的原始的和投影了的特征
• 投影转换矩阵${\mathbf{M}}_{{\varphi }_i}$是基于节点类型的而不是边类型的
• 通过这种特征类型的投影操作，节点级的attention可以处理任意类型的节点

然后，使用self-attention学习各种类型的节点的权重。基于meta-path的节点对$(i,j)$的重要性的计算方式如下：
$$e_{ij}^{\Phi }=at{t}_{node}\left({\mathbf{h}}_i^{\prime },{\mathbf{h}}_j^{\prime };\Phi \right)\text{\hspace{1em}(2)}$$

• $e_{ij}^{\Phi }$表示在meta-path$\Phi$下节点$j$对节点$i$的重要性
• $at{t}_{node}$表示使用节点级注意力的神经网络，给定一个meta-path$\Phi$，所有基于此meta-path的节点对共享$at{t}_{node}$
• $e_{ij}^{\Phi }$是非对称的：$e_{ij}^{\Phi }$和$e_{ji}^{\Phi }$是不同的。因此节点级注意力可以保持非对称性，这是异质图的一个重要性质。

然后，和GAT类似，使用masked attention将结构信息注入到模型中，即只计算中心节点和邻居之间的重要性。得到注意力系数以后使用softmax函数就行归一化：
$${\alpha }_{ij}^{\Phi }={\mathrm{softmax}}_j\left(e_{ij}^{\Phi }\right)=\frac{\exp \left(\sigma \left({\mathbf{a}}_{\Phi }^{\mathrm{T}}\cdot \left[{\mathbf{h}}_i^{\prime }\Vert {\mathbf{h}}_j^{\prime }\right]\right)\right)}{{\sum }_{k\in {\mathcal{N}}_i^{\Phi }}\exp \left(\sigma \left({\mathbf{a}}_{\Phi }^{\mathrm{T}}\cdot \left[{\mathbf{h}}_i^{\prime }\Vert {\mathbf{h}}_k^{\prime }\right]\right)\right)}\text{\hspace{1em}(3)}$$

• ${\mathbf{a}}_{\Phi }$是一个节点级的注意力向量
• 可以看出节点对$(i,j)$的注意力系数${\alpha }_{ij}^{\Phi }$是依赖于它们的特征的
• ${\alpha }_{ij}^{\Phi }$也是非对称的（根据公式的分子分母就可以判断）

基于meta-path$\Phi$的邻居特征聚集如下：
$${\mathbf{z}}_i^{\Phi }=\sigma \left(\sum _{j\in {\mathcal{N}}_i^{\Phi }}{\alpha }_{ij}^{\Phi }\cdot {\mathbf{h}}_j^{\prime }\right)\text{\hspace{1em}(4)}$$

• ${\mathbf{z}}_i^{\Phi }$表示最后节点$i$在meta-path$\Phi$下学到的embedding

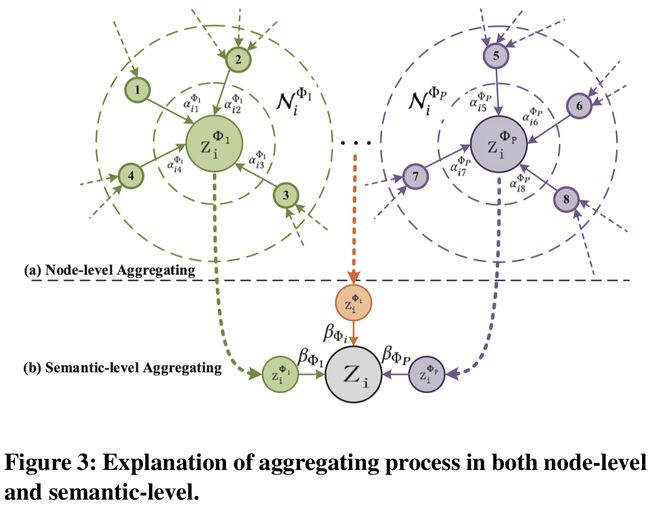
为了使训练过程更稳定，使用multi-head机制，即重复节点级attention$K$次，并将所学到的embeddings进行连接，形成特定语义的embedding：

$${\mathbf{z}}_i^{\Phi }=\underset{k=1}{\overset{K}{||}}\sigma \left(\sum _{j\in {\mathcal{N}}_i^{\Phi }}{\alpha }_{ij}^{\Phi }\cdot {\mathbf{h}}_j^{\prime }\right)\text{\hspace{1em}(5)}$$
给定meta-path集合$\left\{{\Phi }_0,{\Phi }_1,\dots ,{\Phi }_P\right\}$，在进行节点级attention之后，可以得到$P$组特定语义的节点embedings $\left\{{\mathrm{Z}}_{{\mathrm{\Phi }}_0},{\mathrm{Z}}_{{\mathrm{\Phi }}_1},\dots ,{\mathrm{Z}}_{{\Phi }_P}\right\}$。

2.2 Semantic-level Attention

异构图中每个节点包含了很多种类型的语义信息（每个meta-path可以对应一个语义信息）。为了学到更复杂的节点embedding，需要将这些不同的语义信息进行融合。为此，文中提出了一个语义级attention，它可以学习不同的meta-path的重要性并将其融合。语义级attention的输入就是节点级attention的$P$组输出$\left\{{\mathrm{Z}}_{{\mathrm{\Phi }}_0},{\mathrm{Z}}_{{\mathrm{\Phi }}_1},\dots ,{\mathrm{Z}}_{{\Phi }_P}\right\}$，令$\left({\beta }_{{\Phi }_0},{\beta }_{{\Phi }_1},\dots ,{\beta }_{{\Phi }_P}\right)$为每个meta-path学到的权重：

$$\left({\beta }_{{\Phi }_0},{\beta }_{{\Phi }_1},\dots ,{\beta }_{{\Phi }_P}\right)=at{t}_{sem}\left({\mathbf{Z}}_{{\Phi }_0},{\mathbf{Z}}_{{\Phi }_1},\dots ,{\mathbf{Z}}_{{\Phi }_P}\right)\text{\hspace{1em}(6)}$$

• $at{t}_{sem}$表示执行语义级attention的神经网络

为了学到每一个meta-path的重要性，使用一个线性转换（文中使用一层MLP）来转换特点语义的embedding。

文中将学到的特定语义的embeddings度量为使用一个语义级的attention向量$\mathbf{q}$转换了的embedding的相似度：

$$w_{{\Phi }_i}=\frac{1}{|\mathcal{V}|}\sum _{i\in \mathcal{V}}{\mathbf{q}}^{\mathrm{T}}\cdot \tanh \left(\mathbf{W}\cdot {\mathbf{z}}_i^{\Phi }+\mathbf{b}\right)\text{\hspace{1em}(7)}$$

• $\mathbf{W}$表示一个权重矩阵，$\mathbf{b}$表示一个bias向量
• 上面所有的参数对所有的meta-path和特点语义的embedding都是共享的

同样，使用softmax函数对每个meta-path的重要性都进行归一化：

$${\beta }_{{\Phi }_i}=\frac{\exp \left(w_{{\Phi }_i}\right)}{{\sum }_{i=1}^P\exp \left(w_{{\Phi }_i}\right)}\text{\hspace{1em}(8)}$$

最后融合通过不同的meta-path得到的语义级的embeddings：
$$\mathbf{Z}=\sum _{i=1}^P{\beta }_{{\Phi }_i}\cdot {\mathbf{Z}}_{{\Phi }_i}\text{\hspace{1em}(9)}$$

然后，可以使用最终的embeddings进行其他任务。例如，半监督节点分类，基于所有有标签的节点的ground-truth和预测值，最小化交叉熵损失函数：
$$L=-\sum _{l\in {\mathcal{Y}}_L}{\mathbf{Y}}^l\ln \left(\mathbf{C}\cdot {\mathbf{Z}}^l\right)\text{\hspace{1em}(10)}$$

• $\mathbf{C}$表示分类器的参数
• ${\mathcal{Y}}_L$表示有标签的节点的索引
• ${\mathbf{Y}}^l$表示有标签的节点的标签
• ${\mathbf{Z}}^l$表示有标签的节点的embedding

2.3 模型分析

• HAN能解决异构图中多种Node、Relation，以及Semantic融合的问题；
• HAN是高效和易于实现的，可以分别延着每个节点和meta-path并行计算。给定一个meta-path$\Phi$，节点级的时间复杂度为$O\left(V_{\Phi }{F}_1{F}_{2}K+E_{\Phi }{F}_{1}K\right)$，其中$K$表示attention head的数量，$V_{\Phi }$表示节点数量，$E_{\Phi }$表示基于meta-path的节点对的数量，$F_1,F_2$分别是转换矩阵的行数和列数，总的复杂度和节点数量和基于meta-path的节点对的数量呈线性关系；
• 整个模型的Attention是共享的，因此参数的数量不取决于异构图的规模，能够应用于inductive的问题；
• 该模型对于学习节点embedding具有很好的可解释性。基于注意力值，可以检查哪些节点或meta-path对相关任务做出了更高的贡献，这有助于分析和解释实验结果。

3 实验

3.1 数据集

• DBLP
• ACM
• IMDB

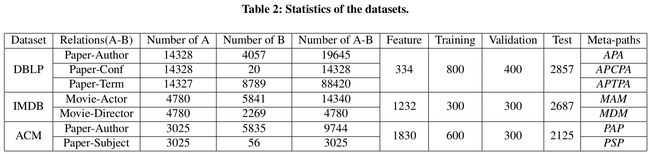
3.2 Baselines

• DeepWalk：为异构图而设计的使用随机游走的网络embedding方法
• ESim
• metapath2vec
• HERec
• GCN
• GAT
• ${\mathrm{H}\mathrm{A}\mathrm{N}}_{nd}$：移除节点级attention的HAN
• ${\mathrm{H}\mathrm{A}\mathrm{N}}_{sem}$：移除语义级attention的HAN
• HAN

3.3 实现细节

3.4 节点分类

• 使用一个$k=5$的KNN分类器进行分类。

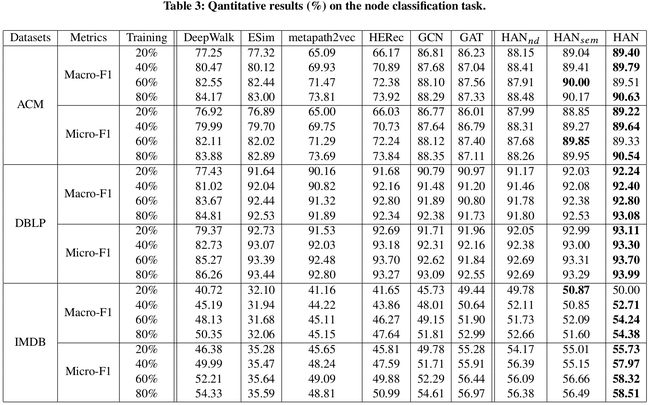
3.5 聚类

• 使用KMeans进行节点聚类，$K$的数量就是节点的种类数。
• 评价指标：NMI、ARI。

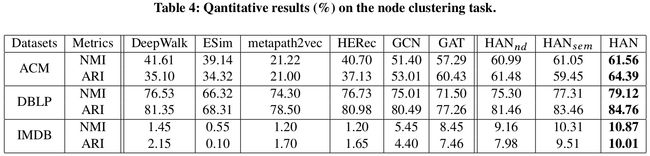
• 相对于当前最优算法，本文所提出的模型表现更好。
• 同时，去除节点级别和语义级别注意力后，模型的效果有不同程度的降低。这验证了节点级别注意力和语义级别注意力的有效性。

3.6 分层注意力机制的分析

node-level attention 分析

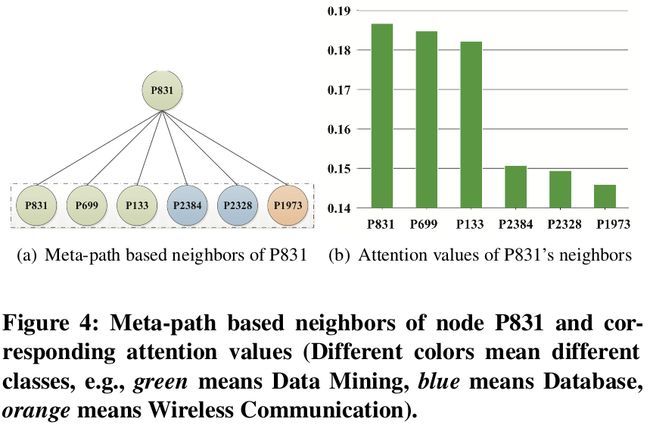
• 节点级注意力赋予了同类型的邻居更高的权重。

semantic-level attention 分析

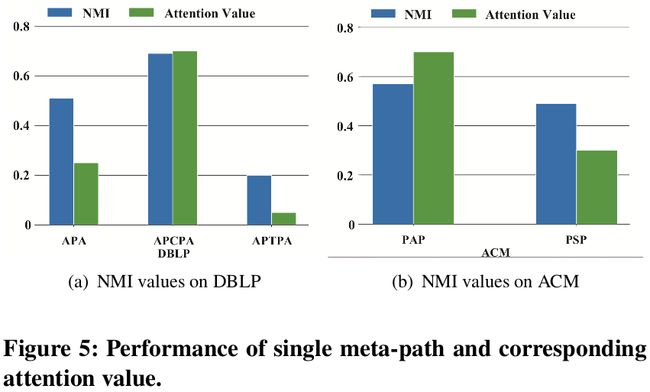
• 在语义级别，对较为重要的meta-path，也就是该条meta-path在聚类任务上具有较大的 NMI 值，HAN 会赋予他们相应较大的权重，因此 HAN 可以自动选取较为重要的节点邻居及meta-path。

3.7 可视化

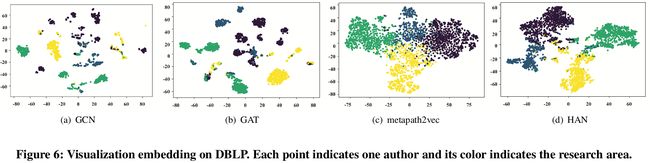
• 可以清楚地看到：HAN 所学习到的节点表示具有更强的表示能力，可以清晰的将不同领域的作者分为 4 类。

3.8 参数分析

• 最终的embedding$Z$的维度：随着维度的增长性能先增后减，说明HAN需要调整出适合的维度
• 语义级attention向量$q$的维度：$q$的维度最好时是128
• attention head $K$的数量：数量增加，HAN性能提升，但是提升缓慢，也使得训练过程更稳定

有错误的地方还望不吝指出，欢迎进群交流GNNs&GCNs（入群备注信息!!!，格式：姓名 -（学校或其他机构信息）- 研究方向）。

4 参考和资源

一个介绍视频：https://www.bilibili.com/video/av53418944/