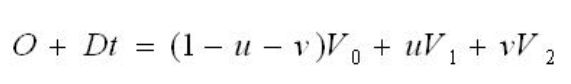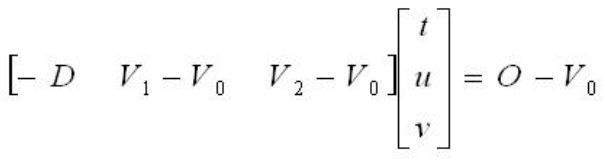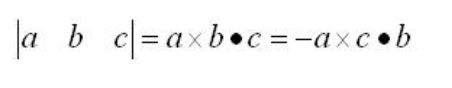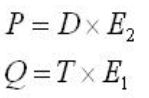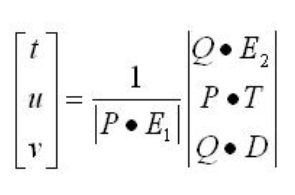基于Qt的OpenGL编程(3.x以上GLSL可编程管线版)---(三十二) 射线拾取RayPicking---(2)拾取三角面
Vries的教程是我看过的最好的可编程管线OpenGL教程,没有之一。但没有讲关于拾取(Picking)的章节,而这个功能的确很重要,就自己试着写写看了。
核心代码“参考”网址如下,别问,问就是抄:
https://www.cnblogs.com/graphics/archive/2010/08/09/1795348.html
PS:博士真难申请!!!!!啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊啊,自闭了??????
Tip1:上节实现了射线,这节写射线与三角面的检测
程序源代码链接:https://pan.baidu.com/s/1ihJt3Jjlu4SfhQEBr3YtoQ 提取码:72l8
编译环境:Qt5.9.4
编译器:Desktop Qt5.9.4 MSVC2017 64bit
IDE:QtCreator
一,程序简介
鼠标点击视口中的任何位置,会生成一条从摄像机(camera)位置,到鼠标点击位置的射线。
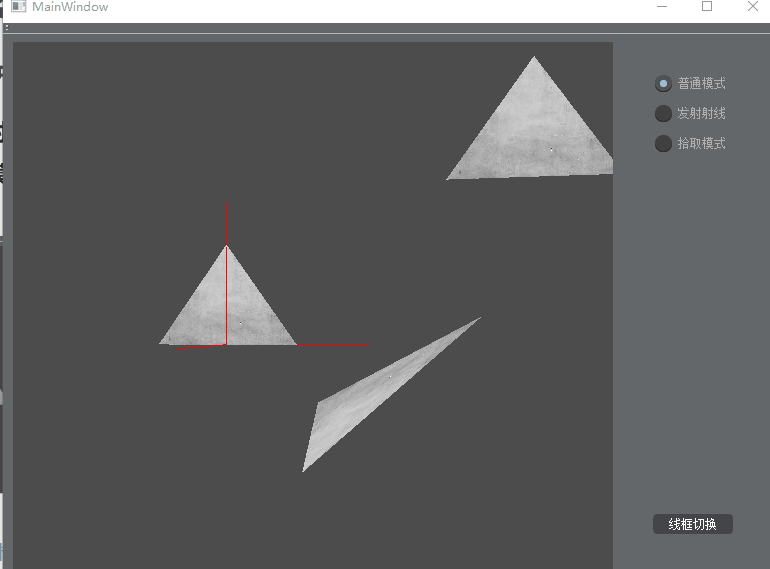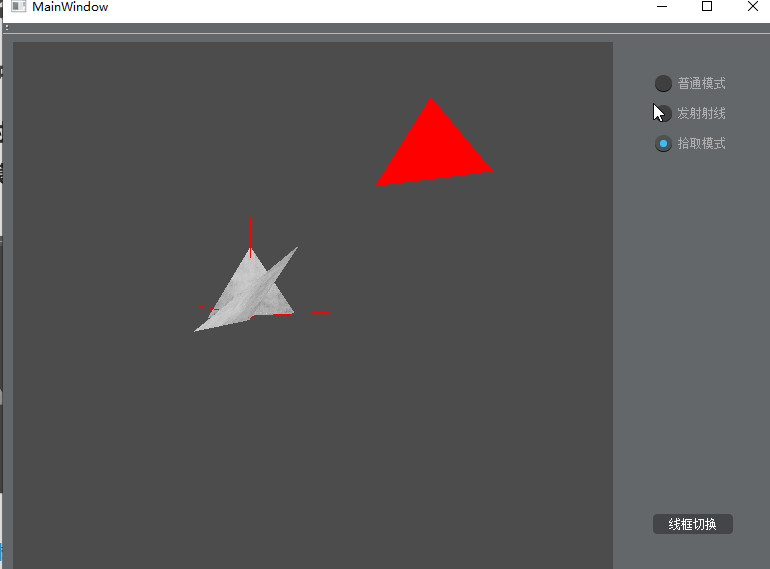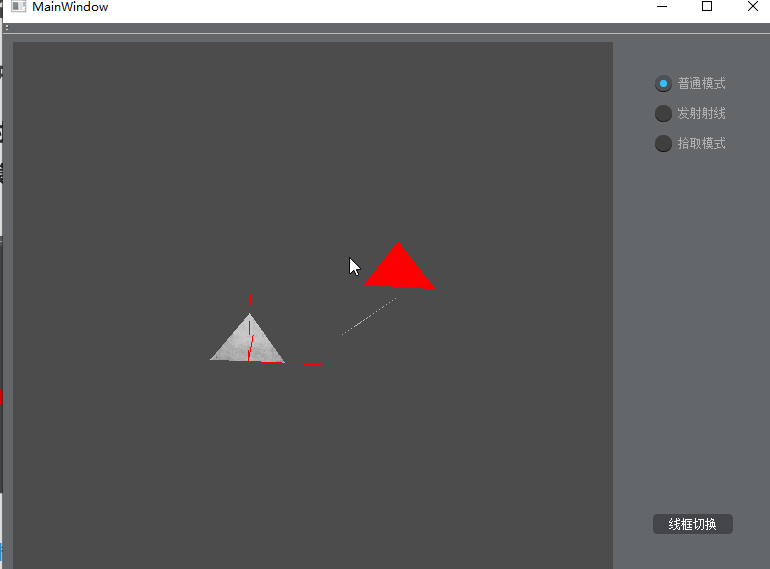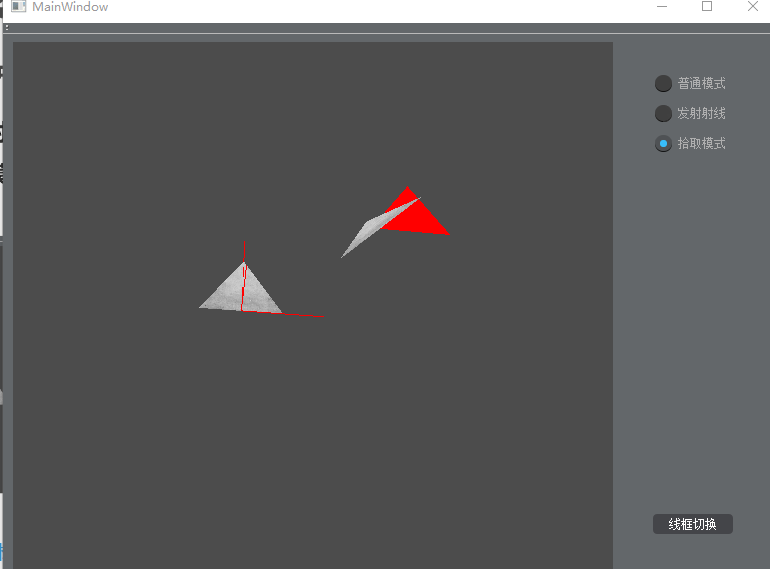
- 在“发射射线”模式下,鼠标左键点击下图所示的位置,会由该摄像机位置生成一条指向该点的射线。
- 在“普通模式”下,WASD控制摄像机前后左右移动,E控制上升,Q下降。鼠标左键按住不放课拖拽摄像机视线方向。
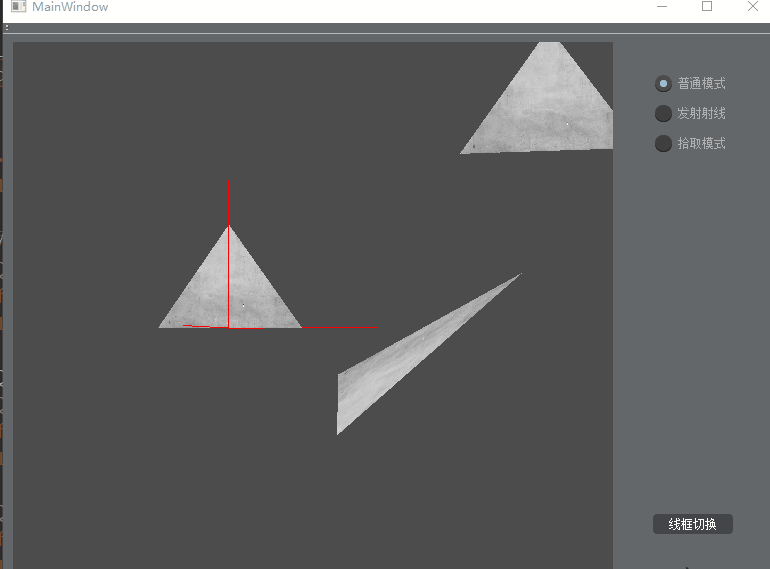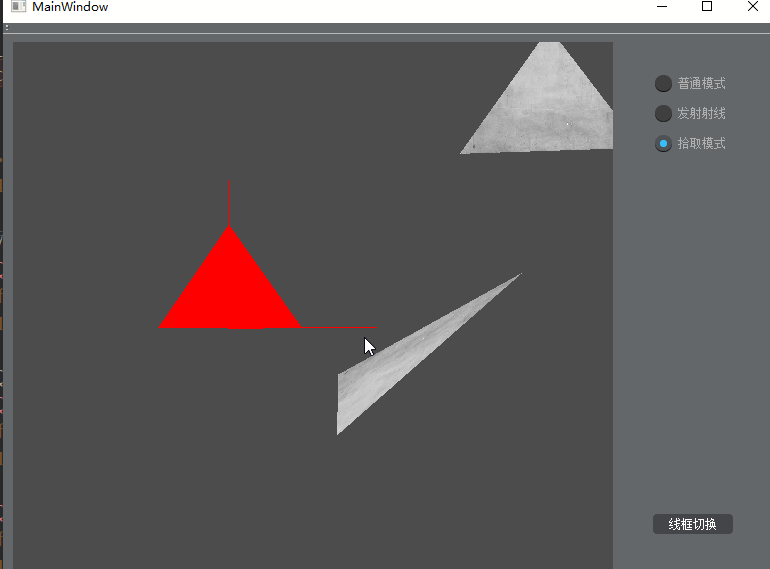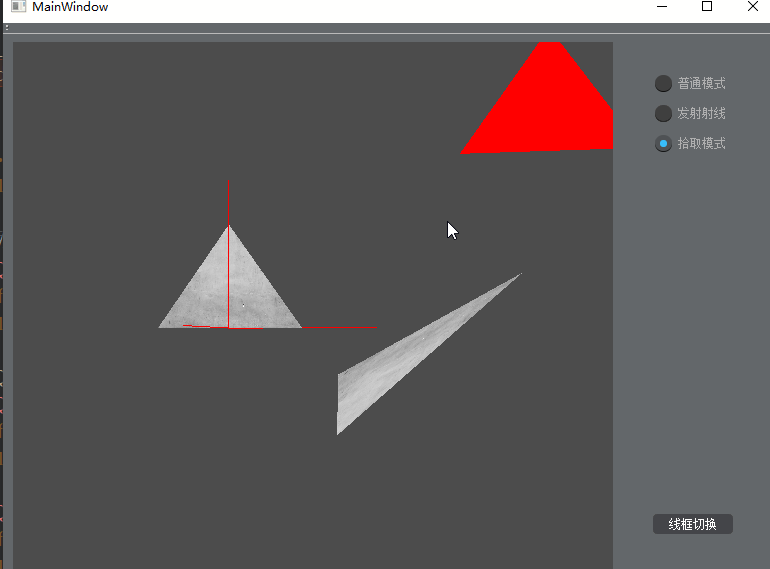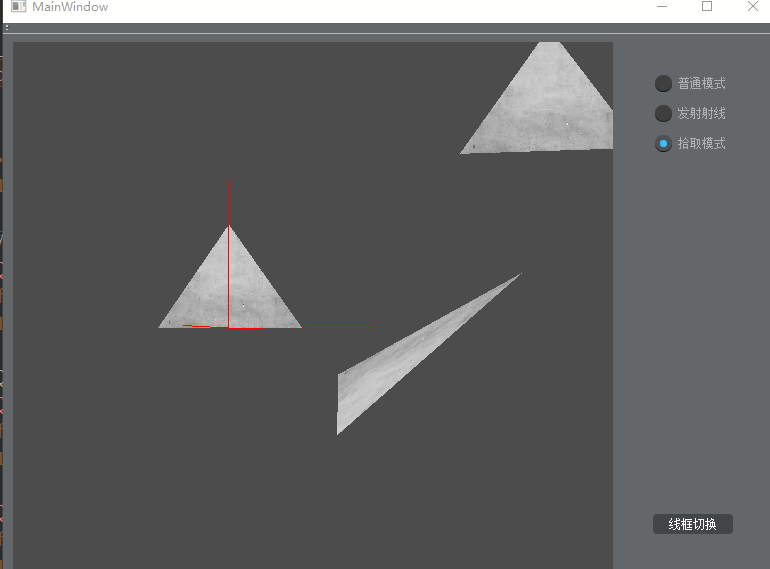
- 在“拾取模式”下,鼠标左键点击屏幕,拾取三角面,被选中的三角面用红色渲染
正常拾取
可拾取距离鼠标点击点最近的三角面
二,数学原理
(以下部分基本照搬引用博客,在细节处加上少许数学上的理解)
(1)射线的参数方程如下,O为原点,即程序中camera的位置, D为射线的单位化方向,即上节求出的射线向量值
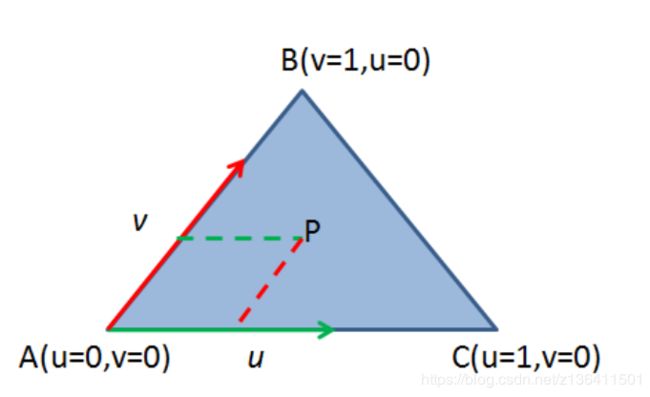
(2)三角形的参数方程如下
三角形所处的平面中,任一点P满足以下方程
P = V0 + u(V1 - V0) + v(V2 - V0) = (1 - u - v)V0 + u V1 + v V2
其中,三角形的A,B,C点坐标已知,V0为A点,V1为C点,V2为B点。
若P点在该三角形内,则该方程需满足:
- 0 < u < 1
- 0 < v < 1
- u + v < 1
条件1和条件2易理解,条件3有两种理解思路
<1> 令w = 1 - u - v,则P = w V0 + u V1 + v V2
w,u,v分别为P所分割的三块三角形面积之比,且w + u + v = 1,如果三者符号不一致,则P点在三角形外(这个证明参考三角形重心坐标的定义与解释),因为u和v大于0,所以w大于0,所以w = 1 - u - v > 0
<2>引用自博客https://www.cnblogs.com/happyEnding/p/7297333.html
取极端情况,当P点在BC边上时,三角形BPP'与三角形ABC相似,则(PP'/AC) = u,所以(P'B/AB) = u,又因为AP' = v·AB,
所以AB = P'B+AP' = u·AB + v·AB,所以u+v=1,所以极端考虑,当P在三角形内时,u+v<1
(3)求射线与三角面的交点,即解联立方程
移项并整理,将t,u,v提取出来作为未知数,得到下面的线性方程组
用两个知识点解该方程组,克莱姆法则与混合积
令E1 = V1 - V0,E2 = V2 - V0,T = O - V0上式可以改写成
(4)运用克莱姆法则,t,u,v变形如下:
克莱姆法则定义:
https://baike.baidu.com/item/克莱姆法则
该法则应用条件为行列式 |-D E1 E2| != 0,理解如下,E1与E2是表示一个面的两个向量,一定是二维的,所以秩R(E1 E2)一定等于2。射线D是三维向量,只有当D与 E1,E2表示的面平行时,R(-D E1 E2) = 2,即 |-D E1 E2| = 0,当然这种平行的情况,本身在程序中就默认判做不选中该三角面,所有当该三角面被选中时,D在第三维度上的分量必定不等于0,即R(-D E1 E2) = 3,|-D E1 E2| != 0。
(5)将三个解,联合起来则有下式
根据混合积公式:
混合积定义:
https://baike.baidu.com/item/混合积
百科上混合积的形式为
|a b c|T = a · (b x c),即矩阵(a, b, c)转置的行列式 = a · (b x c),但用同样的推导方法可推出上面的混合积公式
(6)则方程可改写为
令
可得出t,u,v的最终公式,提出P与Q是为了编程方便
三,程序设计
对解出的t,u,v进行判断,当u,v满足提出的三个条件时
则判定射线与该三角面相交,则该三角面被选中。
在程序设计中,一条射线可能与多个三角面都相交,则这时只需判断处距离射线的发射点最近的一个三角面进行拾取即可,即找出 t 为正值且最小的一个三角形。