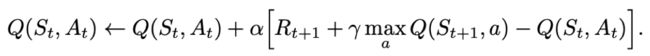从零实践强化学习之基于表格型方法求解RL(PARL)

第二天的课程主要在第一天的基础上开始的,科老师用了很多例子,把许多很难理解的内容讲的非常明白,那我在这里也整理一下,并结合我自己的理解,跟各位分享。

首先是强化学习的四元组

强化学习MDP四元组< S, A, P, R >

这是一个跟时间相关的序列决策问题:

• 在 t-1 时刻,我看到了熊对我招手,那么我下意识的动作即输出的动作是马上逃跑
• 那么在t时刻,熊看到我在跑,就认为发现了猎物,便会发动攻击,这时如果选择装死
• 那么在 t+1 时刻,熊可能会选择离开,这时我们再选择逃跑,那么大概率就能逃跑成功

不过,其实在输出每一个动作之前,都可以有选择的,也就是说,在 t 时刻也可以选择跑路,这时就有一个概率叫作状态转移概率,表示在$S_t$的状态下选择动作$A_t$的时候,转移到下一个状态$S_{t+1}$的概率。

这是符合马尔可夫的,因为状态转移概率是取决于当前的状态$S_t$的,和之前的$S_{t-1}$、$S_{t-2}$都没有关系,并且这个过程也取决于智能体和环境交互的动作$a_t$,这一系列的过程称为马尔可夫决策过程,英文名的缩写就叫做MDP,也就是序列决策的经典的表达方式。

我们可以把可能的动作和可能的状态转移的关系用树状图表示

状态转移与序列决策

画成树状图以后,状态就很明了了:

这是从$S_t$到$S_{t+1}$再到$S_{t+2}$的过程,每次只能走其中一条通路

用P函数和R函数来描述环境:

• P函数表示环境的随机性。举个例子,如果已知 t 时刻选择装死,那么活下去的概率就是 100% 的话,就可以认为这个环境是已知的
• R函数其实是P函数的一部分,表示获得的收益

这里主要讲的是Model-free的情况,即P函数和R函数都未知的情况

Model-free试错探索

强化学习主要解决的就是这种环境未知的情况

• 这里用价值函数V来代表某一状态的好坏;
• 用Q函数来代表什么状态该做出什么动作。

科老师在这里只是简单提了一下,后面会详细讲解

Q表格:状态动作价值

在经过很多次尝试后,我们可以得出一张表即Q表格

我们可以用状态动作价值在表示某个状态下,两个动作哪个更好,至于价值怎么计算,后面会讲到

换一个例子,讲一讲未来的总收益是什么概念:

• 如果有一辆普通的小汽车闯红灯,那么它的收益会减少
• 可如果是一辆救护车,到达医院后可以得到很大的收益,那么这时就应该要闯红灯,因为未来的收益真的很大

现实世界中,这个奖励往往是延迟的,所以一般会从当前时间点开始,对后续可能得到的收益加起来,以此来计算当前的价值

但是有时候目光放得太长远也不好:

对于一个不会结束的任务来说,可能很久以后的收入很大,但这在当下没有意义

股票的例子就很典型了股票要关注累积的收益,如果要把10年后的大涨大跌算进去,把10年后的收益也当作当前动作的考虑因素的话,就没有意义了

解决方法就是:"对远一些的东西当作近视看不见就好"

适当地引入一个衰减因子,再去计算未来的总收益,$\gamma$的值在0-1之间,时间点越久远,对当前的影响也就越小

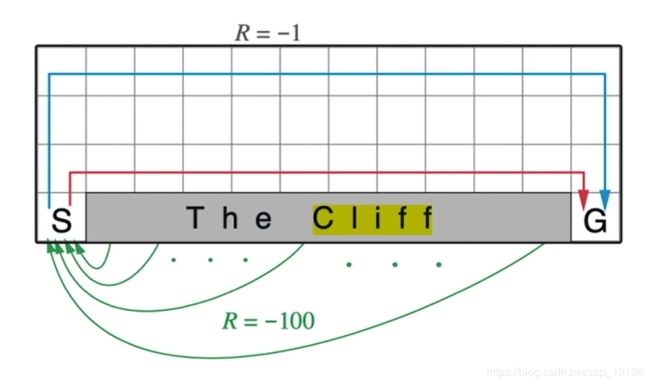
还是强化学习最经典的悬崖问题(快速到达目的地) :

• 每走一步都有-1的惩罚，掉进悬崖会有-100的惩罚(并被拖回出发点)，直到到达目的地结束游戏

下面来看一下在这个例子里怎么计算reward折扣因子γ

reward折扣因子γ

这里做了一个更正,右上角的γ应该是0.6

所以最后要求解的就是这样一张Q表格:

也就是说,Q表格用来指导每一步的动作。并且每走一步,会更新一次Q表格,也就是说用下一个状态的Q值去更新当前状态的Q值

对于Q表格的理解,课堂讨论区里有一位大佬讲的非常清楚:

强化概念:巴普洛夫的条件反射实验

食物对小狗有一种无条件的刺激,而铃声是中性的,一开始并不会对小狗有刺激;而如果在每次喂食前先响一下铃,重复多次后,响铃对小狗来说也会产生一种刺激,会开始流口水,也就是说,声音会代表着有食物,对小狗来说也就有了价值

巴普洛夫实验强调的是中性的条件刺激在跟无条件刺激紧紧挨着的时候,经过反复多次,这种中性的条件刺激也能引起和无条件刺激一样的条件反应

在人的身上可以建立多级的条件反射,举个例子:
  假设人走在树林里,先看到树上有熊爪后看到熊,接着就看到熊发怒了,经过很多次之后,原来要见到熊才瑟瑟发抖的,后来只要见到树上有熊爪就会有晕眩和害怕的感觉。也就是说,在不断地训练之后,下一个状态的价值可以不断地强化、影响上一个状态的价值

科老师也在这里用一个例子做了示范:
https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_td.html

Temporal Difference时序差分(单步更新)

这样的强化方式,其实在数学上只用一行公式就能表示出来:

这个公式想要表达的就是,可以拿下一个Q值来表示当前的Q值

这里的目标值Target就是前面提到的未来收益的累加:

然后用Q($S_{t+1}$,$A_{t+1}$)去近似$G_{t+1}$,最后的目的是让Q($S_t$,$A_t$)逼近这个目标值

这其实就是Sarsa算法:

下面是代码实现的思路:

智能体每次跟环境交互一次以后,就可以从环境当中拿到一个状态和收益(智能体主要依据Q表格选动作),然后拿到这些值以后,就用来更新Q表格

Sarsa算法介绍与代码解析

Sarsa全称是state-action-reward-state’-action’，目的是学习特定的state下，特定action的价值Q，最终建立和优化一个Q表格，以state为行，action为列，根据与环境交互得到的reward来更新Q表格，更新公式为：

Sarsa在训练中为了更好的探索环境，采用ε-greedy方式来训练，有一定概率随机选择动作输出。

obs = env.reset() # 重置环境, 重新开一局（即开始新的一个episode）
action = agent.sample(obs) # 根据 Q表格 选择一个动作

while True:
    next_obs, reward, done, _ = env.step(action) # 与环境进行一个交互
    next_action = agent.sample(next_obs) # 根据算法选择一个动作
    # 训练  Sarsa 算法
    agent.learn(obs, action, reward, next_obs, next_action, done) # 更新 Q表格 
    action = next_action
    obs = next_obs  # 存储上一个观察值

这里的sample()函数用的是ε-greedy的方式:

它其实就是探索和利用的方法,举个例子,如果你去到一家餐厅,你可以利用你以前的经验选一道菜,这样可以保证你点的菜不会不合你的胃口;但是你也可以探索这家店的其他你没吃过的菜,那你就有可能吃到更好吃的菜肴,也有可能吃到不符合你胃口的菜肴

如果训练的过程中只从Q表格里选择,那么可能无法得到更优的结果,况且一开始训练时,Q表格是不准确的

# 根据输入观察值，采样输出的动作值，带探索
def sample(self, obs):
    if np.random.uniform(0, 1) < (1.0 - self.epsilon): #根据table的Q值选动作
        action = self.predict(obs)
    else:
        action = np.random.choice(self.act_n) #有一定概率随机探索选取一个动作
    return action

# 根据输入观察值，预测输出的动作值
def predict(self, obs):
    Q_list = self.Q[obs, :]
    maxQ = np.max(Q_list)
    action_list = np.where(Q_list == maxQ)[0]  # maxQ可能对应多个action ,所以随机选择一个
    action = np.random.choice(action_list)
    return action

所以训练的时候用的是sample()方法,即除了要拿到最优的动作,我们还要保证其他的动作能有一定的概率被探索出来

这是Sarsa与环境交互的流程图:

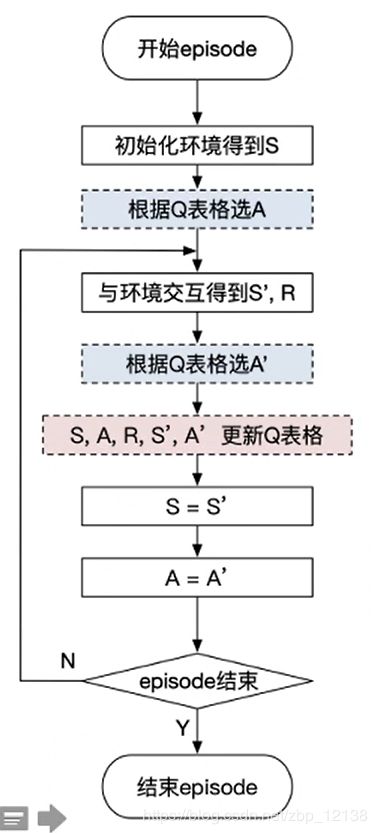
最主要的其实就是更新Q表格的方法:

# 学习方法，也就是更新Q-table的方法
def learn(self, obs, action, reward, next_obs, next_action, done):
    """ on-policy
        obs: 交互前的obs, s_t
        action: 本次交互选择的action, a_t
        reward: 本次动作获得的奖励r
        next_obs: 本次交互后的obs, s_t+1
        next_action: 根据当前Q表格, 针对next_obs会选择的动作, a_t+1
        done: episode是否结束
    """
    predict_Q = self.Q[obs, action]
    if done:
        target_Q = reward # 没有下一个状态了
    else:
        target_Q = reward + self.gamma * self.Q[next_obs, next_action] # Sarsa
    self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q

公式里的α就是学习率learning_rate,代码也是完全按照公式写的,另外,如果一个回合结束了,就没有下一个状态了,这一步代码要记得加上,否则可能无法收敛

Sarsa用的是on-policy的策略,在做悬崖问题时,他会努力避开悬崖,虽然路程远了,但至少掉下悬崖的风险就小了很多

on-policy与off-policy对比

• on-policy优化的实际上是它实际执行的策略,用下一步一定会执行的动作action来优化Q表格,所以on-policy其实只存在一种策略 ,用同一种策略去选取和优化

• off-policy实际上有两种不同的策略,期望得到最佳的目标策略和大胆探索的行为策略
  

off-policy通过行为策略,把所有可能的策略输入目标策略,这里输入给目标策略的数据里不需要$a_{t+1}$,因为目标策略不需要管下一步要往哪里走,它只选择收益最大的策略

行为策略就像是一位天不怕地不怕的战士,可以在环境里面尝试所有的动作,并将得到的经验交给目标策略学习。

所以目标策略就像是一个在后方指挥的军师,它可以根据经验学习到最优的策略

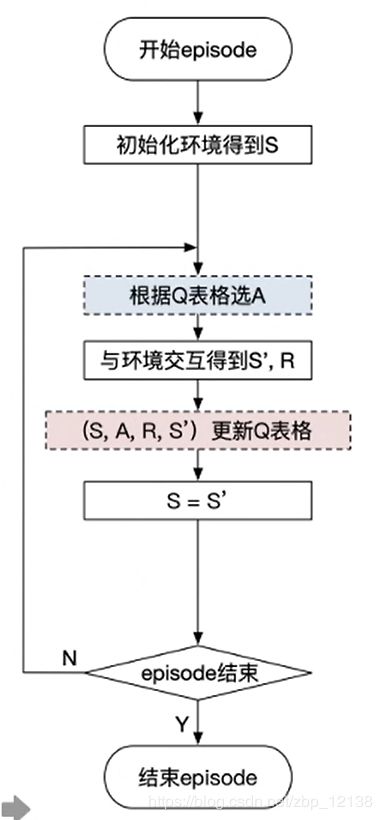
Q-learning解析

Q-learning也是采用Q表格的方式存储Q值（状态动作价值），决策部分与Sarsa是一样的，采用ε-greedy方式增加探索。

• Q-learning跟Sarsa不一样的地方是更新Q表格的方式。
• Sarsa是on-policy的更新方式，先做出动作再更新。

Q-learning是off-policy的更新方式，更新learn()时无需获取下一步实际做出的动作next_action，并假设下一步动作是取最大Q值的动作。

Q-learning的更新公式为：

说的直白一些就是Q-learning不需要把$A_{t+1}$传进来

他们的区别只在Target的计算上:

Q-learning默认了下一个动作就是Q最大的动作,它并不受探索的影响,只按照最优的策略寻找最优的路径

所以在悬崖问题里使用Q-learning时,智能体往往会表现得比较大胆,他会贴着悬崖的边行进

Q-learning与环境交互的流程图:

下面看一下Q-learning的代码:

 # 学习方法，也就是更新Q-table的方法
    def learn(self, obs, action, reward, next_obs, done):
        """ off-policy
            obs: 交互前的obs, s_t
            action: 本次交互选择的action, a_t
            reward: 本次动作获得的奖励r
            next_obs: 本次交互后的obs, s_t+1
            done: episode是否结束
        """
        predict_Q = self.Q[obs, action]
        if done:
            target_Q = reward # 没有下一个状态了
        else:
            target_Q = reward + self.gamma * np.max(self.Q[next_obs, :]) # Q-learning
        self.Q[obs, action] += self.lr * (target_Q - predict_Q) # 修正q

跟Sarsa不同的就是这句,直接获取Q的最大值:

target_Q = reward + self.gamma * np.max(self.Q[next_obs, :]) # Q-learning

代码演示

代码在PARL的examples里:

进入lesson2就可以看到代码了,这里放动图给大家对比一下

Sarsa

很明显,Sarsa走的路径要长一些:

Q-learning

而Q-learning的路径是最短的: