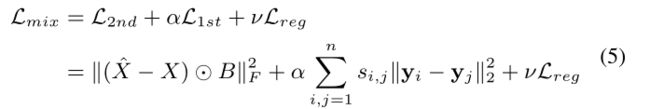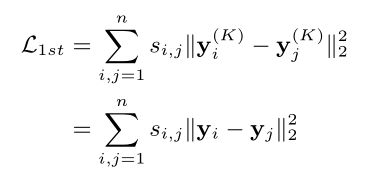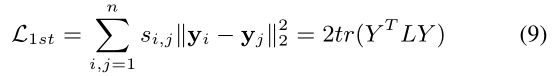SDNE（Structural Deep Network Embedding）理论及pytorch实现

SDNE 使用自动编码器（AutoEncoder）结合拉普拉斯特征映射(Laplacian Eigenmaps），针对网络结构非线性，构建多层非线性函数深度模型，同时针对全局和局部结构以及稀疏性问题，同时优化一阶相似性和二阶相似性来学习网络的局部结构信息和全局结构信息。

一、基础定义

相似度定义

（1）一阶相似度定义：成对节点之间的相似性 或者 节点与其近邻节点的相似性。一般可以用邻接矩阵$S$中的一行$S=\{s_{i,1},s_{i,2},...,s_{i,|V|}\}$，表示$v_i$与其他节点之间的相似度。如果$s_{i,j}>0$，则$v_i$与$v_j$之间存在正的一阶相似度。如果节点之间没有连接，则一阶相似度为0.
（2）二阶相似度定义：一对节点的领域结构的接近程度。$v_i$与$v_j$之间的二阶相似度可以定义为：邻接矩阵中$s_i$和$s_j$之间的相似性。可以简单理解节点与节点之间相同的邻居节点数来刻画二阶相似性。

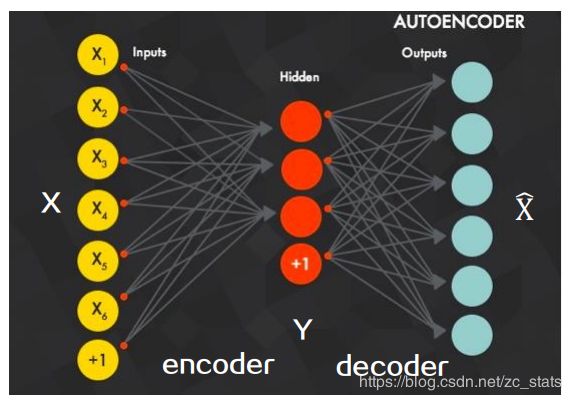
自编码器

将input压缩为Hidden的部分称为encoder，将hidden还原为input的部分称为decoder。SDNE使用deep autoencoder来获得节点二阶相似度信息

拉普拉斯特征映射 (Laplacian Eigenmaps）

-通过平滑项的方式，使得在原始空间中两个相似的节点，在低维的向量空间中有相近的表示。
-最小化的目标函数如下：

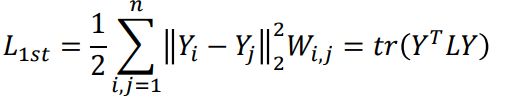
-其中$L=D-W$，称$L$是图G的拉普拉斯矩阵，$D\in R^{n\times n}$是图G的节点的度，$D_{i,i}={\sum }_j{W}_{i,j}$，W为图的邻接矩阵。
-该优化问题可以转化为拉普拉斯矩阵的特征向量计算问题

二、网络结构

三、损失函数

论文中一些字符代表含义

模型的损失函数：

其中，使用L2正则，防止过拟合

对损失函数的解释

1.使用deep autoencoder 学习网络二阶相似度信息

考虑到邻接矩阵中很稀疏，如果直接将领接矩阵的第$i$行$S_i$作为$x_i$传入autoencoder中会导致重构的领接矩阵$S^{\ast }$中有很多0。进行如下改进，对重构误差中非零的元素增加更多的惩罚。

其中$⨀$，表示哈达玛积（对应元素相乘），如果为$s_{i,j}$ 为0，则$b_{i,j}=1$，否则$b_{i,j}=\beta >1$。
通过自动编码器后，如果两个节点具有相近的领接点结构，则在嵌入后的向量表示空间中距离越近。

2.使用拉普拉斯特征映射（Laplacian Eigenmaps），学习网络一阶相似度信息

可以通过化简得到（9）

3.加入L2正则，防止过拟合

三、优化

这部分主要是参数优化，对损失函数中参数的求解过程

四、算法

输入网络G的领接矩阵和参数，通过深度信念网络得到初始化参数，然后放入深度神经网络中训练

五、实现

根据大佬的TensorFlow版本实现了一波pytorch版本
https://github.com/CyrilZhao-sudo/SDNE

embedding之后，降维后的效果

下面是用embedding之后进行多分类任务的效果：

‘micro’: 0.5945945945945946	‘macro’: 0.42586056451041765
samples’: 0.5945945945945946,	‘weighted’: 0.5764363234018914,
‘acc’: 0.5945945945945946

优缺点

优点： 深层网络嵌入模型；缺点：当网络中添加新节点时，如果未观察到新节点与现有节点的连接，则无法给出新节点的嵌入向量

参考：
https://www.isclab.org.cn/wp-content/uploads/2019/03/%E7%BD%91%E7%BB%9C%E8%A1%A8%E7%A4%BA%E5%AD%A6%E4%B9%A0-SDNE-%E5%91%A8%E5%A6%8D%E6%B1%9D-2019-03-24-19_00_00.pdf
https://zhuanlan.zhihu.com/p/56637181
https://github.com/shenweichen/GraphEmbedding