大话西游之王道考研数据结构第十讲---查找

 

复习

1. prim、kruskal、dijkstral复杂度分别是多少？
2. 如何判断一个图是连通的？DFS遍历一次输出的是图中什么内容？
3. 无向图中删除某个顶点的复杂度是多少（用邻接链表存）？
4. 是什么造成拓扑排序不唯一？
5. 关键路径的五个函数都应该怎么求？

一、查找

查找其实对我们来说并不陌生，我们在线性表中学过查找某个元素的复杂度是多少（顺序表示是多少，链式表示是多少？），我们之前也学过二叉排序树，二叉排序树的构建其实就是为了更方便的动态查找（二叉排序树的查找复杂度是多少？）。这里我们将系统的学习所有的查找方式。

在数据集合中寻找满足某种条件的数据元素的过程称为查找。查找的结果一般分为两种，查找成功和查找失败（还记得我们在二叉排序树里面，计算了两种平均查找长度 ASL成功和ASL失败,还记的ASL失败是怎么计算的么？）。

1.1 顺序查找

这个其实就是线性表的查找方式，

int Search_Seq(int a[],int n, int key){
    for(int i =0;i

这里提供两种查找代码，第一种是我们一般采用的方式，第二种是书上提供的更骚的套路。第二种理解下这么妖娆的操作是怎么实现的。二者在复杂度上面没有变化，但是代码执行次数上面，第二种更快一点（就像 3*n 和 2*n 的复杂度都是n一样）。下面的ASL都是按照第二种查找方式计算的

ASL_成功 = （n+1）/2;

（假设每个元素查找概率相同，第一个元素查找1次 第n个元素查找n次，总共查找 ((1+n)*n/)2,平均的话再/n就好了）

ASL_失败 = n+1

（因为查找失败时候，我们需要查找到第0个元素，所以总共对比的元素有n+1个，如果按照第一种方式，查找失败是多少？，考试时候，正确答案是第二种的查找，第一种就不要记了，这里加上第一种只是为了更深刻的理解查找失败长度计算过程）

1.2 有序表的顺序查找

我们待查找的序列是有序的，假设是递增有序，这就相当于，二叉排序树里面只有左结点了。这时候查找成功和失败就是二叉排序查找成功和失败的方式：
            ASL_成功 = （n+1）/2;

 ASL_失败 = (1+２+3+...+n+n)/n = n/2 + n/(n+1)

有序查找可以是顺序表示，也可以是链式表示

1.3 二分查找（也是折半查找）

它和顺序查找一样，也要求查找表示有序的，但是它只适用于顺序表，因为他需要找到查找表里面，中间的元素，如果是链式表的话，这样找到中间元素都是O(n),而顺序表示是O(1)。所以只适用于顺序表。

其核心思想和高中学的最小二乘法逼近函数答案差不多，待查找的查找表a的区间是[l，r]，最中间的是mid = (l+r)/2 我们看下a[mid]和要查找的元素大小比较，如果小的话，说明应该落在[mid+1,r]里面，如果大的话因该落在[l,mid-1]里面，如果相等的话直接输出

void Binary_Find(int t,int n)
{
    int l = 1;
    int r = n;
    int mid;
    while(r>=l)
    {
        mid = (l+r)/2;
        if(a[mid]t)
        {
            r = mid-1;
        }
    }
    a[r+1] = t;
}

二分查找的图表示其实就是一颗平衡二叉树

这里面的计算用到了高数里面无穷级数那一章里面的内容，刚好可以把那一章复习一下，并且终于明白那一章不仅难，还有点用。。。

所以折半查找的复杂度是，而顺序查找是，所以折半查找好一点

1.4 分块查找

分块查找结合了顺序查找和折半查找的优点，需要另外开辟一个索引表，把n个元素分为k块，索引表长度为k，索引表中的元素，代表对应块中最大元素。在索引部分采用折半查找，内部采用顺序查找。

所以总共的平局查找长度应该分为两部分,设索引查找和块内查找的平均查找长度为

设将长度为n的超找表均匀的分为b块，每块有s个记录，在等概率的情况下，若在块内和索引表中均采用顺序查找，则平均查找长度为：

此时，若 则式子可以取到最小值：

如果对索引采用折半查找时候，平均长度为：

二、散列表（Hash表）（大题必考）

如果我们想查询一个表里有没有元素k，如果这个表是无序的，那么复杂度应该是O(n),就算是有序的，顺序查找是O(n)，折半查找是。这些都是基于比较的查找方式，查找的效率取决于比较的次数，那么有没有可能让他变成O（1）呢？

Hash的意义在于把一个大的集合A，映射到小的集合B，这样查找起来会更省时。哈希表是根据关键字直接进行访问的数据结构。我们通过散列函数，把关键字映射到对应的函数中。散列函数可能会把两个或两个以上的不同关键字映射到同一地址，称这样的情况为“冲突”。

1.1 散列函数的构造方法

           除留余数法：假定散列表的表长为m,取一个不大于m但最接近或等于m的质数p,利用一下公式吧关键字转换成散列地址。散列函数为

                                                                                                  

1.2 处理冲突的方法

1. 开放定址法

            这个需要把数据放在数组里面

                                                                                           

           这个d的确定有好几种方法，比如d每次增加1，或者每次变为平方，或者换个哈希函数，或者随机选一个。

a.线性探测法：发现冲突时候，一个一个往后挪，直到找到空位子坐下~但是这样会造成大量元素在相邻的散列地址上"聚集”（堆积），大大降低查找效率。

b.平方探测法：,其可以避免堆积，但是不能探测到散列表上所有单元，但至少能探测到一半单元。

c.再散列法：发现冲突以后，通过另一个函数，重新选取位置，直到不发生冲突为止。

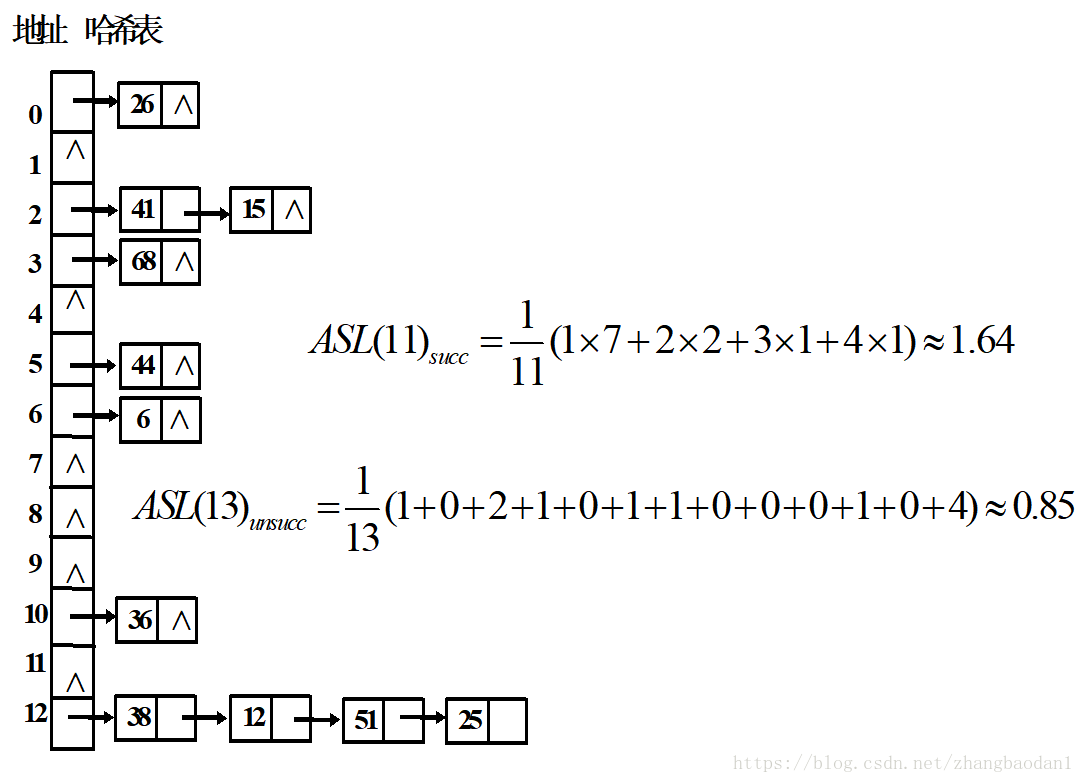
2.拉链法

这个就有点像链表了，所以你会发现数据结构过来过去，存储方式就这俩种，很多地方都是通的。

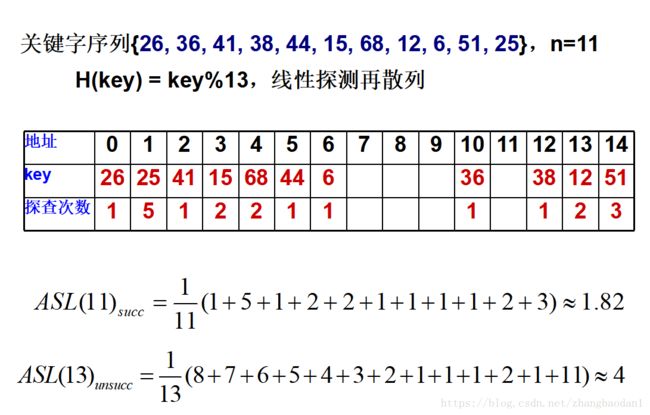
1.3 ASL成功和失败

1.哈希表中一共有四个主要参数，p,n,m,a。其中p是待取模的质数，m是整个表的长度，n是元素的个数，a是装填因子

2.哈希表采用开放地址法时候，查找失败的分母取决于p而不是m。

2.哈希的查找性能，即平均查找长度依赖于哈希表的装填因子a，不直接依赖于 n 或 m。

3.拉链法中，查找失败有两种不同的计算方式，这里我们采用教材规定的上面那种。

三、字符串匹配

字符串匹配的含义就是检测要查找的字符串T在不在被查找的字符串S里面。这就和word里面的ctrl+f的功能一样（这个功能可能是用优化以后的KMP或者SUNDAY、BM算法写的,SUMDAY是一个非常好理解的，且效率比KMP要高的算法，如果你喜欢这一块的话，可以了解下这个算法）。

这里，容易想到的一个简单的算法就是一个一个比算法，在S中挨个查找，如果某个位置往后和T能够完全匹配，就返回这个位置，如果不行，就看下这个位置的下一位，直到S字符串全部检查完毕。

3.1 简单的模式匹配算法

int Index(char s[],int sum_s,char t[],int sum_t){
    int i = 1,j = 1;
    while(i <=sum_s&&j<=sum_t){
        if(s[i] == t[j] ){
            i++;
            j++;
        }
        else{
            i = i-j+2; 
            j =1;
        }
    }
    if(j >= sum_t){
        return i - sum_t;
    }
    else return 0;
}

3.2 改进的模式匹配算法-KMP算法

KMP算法算是本科里面学到过的最难理解的算法之一了，当初也是花了很长时间去学习这个东西，那个时候虽然搞懂了，但是现在又给忘了，而KMP刚好考研时候只考NEXT数组的计算方式（完全弄懂KMP对于只应付我们学校初试来说，没有太大必要）。NEXT数组里面：

1.next[1] = 0,next[2] = 1

2.后面每一个来说，只需要看看其前面的数组里面，前缀后缀重复的最大长度是多少，然后加1就好了，比如计算NEXT[6]时候，前面最大前缀是ABA，后缀是ABA 所以NEXT[6]=  3+ 1 = 4

编号	1	2	3	4	5	6	7	8	9	10	11	12
S	A	B	A	B	A	A	A	B	A	B	A	A
Next	0	1	1	2	3	4	2	2	3	4	5	6