交叉熵、KL散度、极大似然估计与最大后验估计
参考资料:
【知乎】信息熵是什么?————YJanjo的回答
熵和编码长度
熵(Entropy),交叉熵(Cross-Entropy),KL-松散度(KL Divergence)
详解最大似然估计(MLE)、最大后验概率估计(MAP),以及贝叶斯公式的理解——nebulaf91
【知乎】极大似然函数、最小二乘、交叉熵之间的联系
深度学习中交叉熵和KL散度和最大似然估计之间的关系
前言
交叉熵与KL散度是两个很相似的概念,极大似然估计与最大后概率验估计也经常被相互比较,交叉熵与极大似然估计更是有千丝万缕的联系。这篇文章就把这四个概念放在一起讲解,目的是从数学角度理清这四个概念的联系与区别。本文首先从信息论中的信息熵出发,然后逐渐引出交叉熵、KL散度、极大似然估计和最大后验概率估计。
信息熵
介绍信息熵的文章很多,浅一点的会从定性的角度阐述信息量与信息熵的概念及联系,深一点的是从编码长度的角度解释信息熵的公式到底是怎么来的,论证出“熵代表着根据信息的概率分布对信息编码所需要的最短平均编码长度”这个结论。这些当然都是正确的,但好像又有点生涩,读完后多多少少有点似懂非懂。
概念理解
这里先从概念角度做一个大致的说明。熵在热力学中表示物体的混乱程度,在信息论中则表示事务的不确定性。信息量与信息熵是相对的,告诉你一件事实,你获取了信息量,但减少了熵。或者说,得知一件事实后信息熵减少的量,就是你得到的这个事实所包含的信息的量。
公式本质
说到“量”这个字,第一想到的就是他是应该有单位的,而“单位”这个东西其实是从“参照物”衍生出来的。3kg的东西之所以是3kg,是因为国际上拿了一金属块,统一规定了它的重量就是1kg,这个金属块便成了“参照物”。信息熵、信息量也是有参照物的,那就是“硬币”。一块均匀的硬币,不考虑竖起来,可以等概率掷出两种可能——正和反。那么一件事情,如果有两种等概率的可能,那它就能用1个硬币来描述,此时它的熵就是1bit。没错,熵代表不确定性,这个不确定性有多大,就看能拿几个硬币来描述,这个硬币便是参照物了。
那么1个硬币描述2种等概率可能的事务,2个硬币自然可以描述有4种等概率可能的事务。那么3个硬币呢?不是6,而是8,因为你抛3个硬币,最多能出来8种结果。所以熵的计算就不能和质量一样简单的做除法,而是要做log。
硬 币 个 数 = l o g 2 ( 可 能 出 现 几 种 情 况 ) 硬币个数=log_2(可能出现几种情况) 硬币个数=log2(可能出现几种情况)这个公式是有一个前提条件的——所有事件等概率,因为参照物“硬币”也是均匀等概率的。但世间的真实存在的事务往往不是等概率的。
用最常用的考试选择题来举例。选择题ABCD不是等概率的,要不也不会出现“不会就选C”这种说法。假设经过大数据统计,某学校出的试卷选择题的概率如下表,那么此时选择题的熵应该为多少?
| 选项 | 概率 |
|---|---|
| A | 1 4 \frac{1}{4} 41 |
| B | 1 8 \frac{1}{8} 81 |
| C | 1 2 \frac{1}{2} 21 |
| D | 1 8 \frac{1}{8} 81 |
这种情况下肯定无法用上面那个公式了,因为四种情况不是等概率的。此时应该分别计算四种情况的熵,然后利用其概率加起来,如下式:
总 熵 = 1 4 ∗ A 的 熵 + 1 8 ∗ B 的 熵 + 1 2 ∗ C 的 熵 + 1 8 ∗ D 的 熵 总熵=\frac{1}{4}*A的熵+\frac{1}{8}*B的熵+\frac{1}{2}*C的熵+\frac{1}{8}*D的熵 总熵=41∗A的熵+81∗B的熵+21∗C的熵+81∗D的熵但分别的熵怎么计算?
选A的概率为 1 4 \frac{1}{4} 41,所以可以单独将选项A看作一个结果为4类的事件,且四种结果是等概率的。 此时A的熵就可以用以下式子表示:
A 的 熵 = l o g 2 4 A的熵=log_24 A的熵=log24同理,BCD的熵就可以分别表示为 l o g 2 8 、 l o g 2 2 、 l o g 2 8 log_28、log_22、log_28 log28、log22、log28。
得到以上结果的一个原则是将每个选项根据其概率单独看作一个含n种等概率结果的事件,n就是每个选项概率的倒数,那么单个选项的熵就可以写为:
P ( x ) l o g 2 ( 1 P ( x ) ) P(x)log_2(\frac{1}{P(x)}) P(x)log2(P(x)1)把所有选项加起来就得到了熵的公式:
H ( x ) = − ∑ i = 1 n P ( x i ) log 2 P ( x i ) H(x)=-\sum_{i=1}^{n} P\left(x_{i}\right) \log _{2} P\left(x_{i}\right) H(x)=−i=1∑nP(xi)log2P(xi)再从经常提到的编码角度来理解一下,编码其实和硬币是一样的,硬币的正\反就是编码中的0\1。编码规定只能出现0或1,所以一个编码位置就只有两种情况——要么是0要么是1,也就是一枚硬币了。
所以,上面提到的,需要用几枚硬币来描述,这里就变成了需要多长(多少位置)的编码来描述。还记得刚开始提到的结论吗?熵代表着根据信息的概率分布对信息编码所需要的最短平均编码长度,这个“平均”这个词就是指代的熵公式中的数学期望。(关于数学期望不懂得自己去补课)那为什么是最短编码长度呢?
假设要作弊传答案,规则是只能用编码的方式传递,也就是说只能用0\1,如果传递一个位置的编码需要100块钱,那么如何将成本最小化呢?答案就是熵。如果无视ABCD的概率问题,用两个编码位置来传答案,也就是说无论答案是什么都用两个位置去传,方式为00代表A、01代表B、10代表C、11代表D,计算数学期望,这波传答案的操作的编码长度的期望为:
1 4 ∗ 2 + 1 8 ∗ 2 + 1 2 ∗ 2 + 1 8 ∗ 2 = 2 \frac{1}{4}*2+\frac{1}{8}*2+\frac{1}{2}*2+\frac{1}{8}*2=2 41∗2+81∗2+21∗2+81∗2=2平均下来,传递一个答案需要的成本为200块,简直贵的一批!
考虑将概率大的选项用更短的编码去传答案,因为它出现的频繁,用长编码会贵。将概率小的选项用长编码去传答案,别问为啥不能都用短的编码表示,因为编码只有0\1,短编码表示的情况种类有限,不可能都用短编码。经过上面的计算,ABCD分别需要的编码长度为 l o g 2 4 、 l o g 2 8 、 l o g 2 2 、 l o g 2 8 log_24、log_28、log_22、log_28 log24、log28、log22、log28,也就是2、3、1、3,可以考虑如下编码:
| 选项 | 编码 |
|---|---|
| A | 10 |
| B | 111 |
| C | 0 |
| D | 110 |
这样算下来编码长度的期望为1.74bit,需要花费174块,好像也没便宜多少。能不能更便宜呢?不能!
此时你应该提出疑问,如果用1表示A,10和01分别表示B和D,那不就更短了吗?这里不能这么理解,这里的编码长度是与二叉树有联系的,其中隐含了事件概率大小的排序关系 ,这是其一。其二是如果你采用上面所谓的更短的编码,你反推回去,ABCD概率加起来必然就不是1了,所以说来说去其实还是那句,编码长度中蕴含了概率信息,概率在前提上约束了编码长度。
再举一个不恰当的例子来深化一下与二叉树的联系。这里传答案这个操作不能理解为直接告诉你答案是哪个,传答案应该理解为告诉你是不是这个选项。 因为C选项出现的概率最大,所以第一位先告诉你是不是C?如果传给你0,那就是C,否则不是,这才是给C编短码的意义所在。如果答案传过来不是C,那继续告诉你是不是A,因为A是第二大概率的,这里我不可能直接去告诉你是不是D,D相对来说是小概率事件,第二个就判断实在是浪费。第二位如果是0,那么就是A,如果是1,那么不是A,所以A的编码为10。B和D的编码自然也能理解了。(这其实有点像霍夫曼编码,感兴趣的可以了解一下)
这只是一个不恰当的例子!
这只是一个不恰当的例子!
这只是一个不恰当的例子!
重要的事情说三遍。事实上如果B编码为101,D的编码为100也行,当然A也可以用01,C也可以用1,上面例子只是为了让你理解编码长度本身这件事,以及继续强调编码长度蕴含概率信息这个结论。至于编码内容只是这个例子不可避免附带进来的概念,不用深究。
这里还有一个问题,如果有个概率为0.3的事件,那么我们也不知道该如何用一个 − l o g 2 ( 0.3 ) = 1.74 -log_2(0.3)=1.74 −log2(0.3)=1.74个bit的二进制编码表示。上面的例子主要是为了让你理解熵的一个计算过程,最后终究还是要回到本质——熵表示不确定性,这种计算方式推广、抽象开来后结果也是表示不确定性的大小而已,生活中的例子肯定不能解释出所有的细节。
交叉熵
上面说过,假如说我们用这个分布来作为我们来对事件编码的一个工具,熵就衡量了我们用这个正确的分布y来对事件编码所能用的最小的bit 长度,我们不能用更短的bit来编码这些事件或者符号了。(如果有更短反推概率和一定不为1)
相对的,交叉熵是我们要对y这个分布去编码,但是我们用了一些模型估计这个分布,并且得到了估计值 y ^ \hat y y^,那么的最小编码长度就变成了 l o g ( 1 y ^ i ) log(\frac{1}{\hat y_i}) log(y^i1),但是呢,我们的期望仍是关于真实分布y的。所以交叉熵的定义就变成了:
H ( y , y ^ ) = − ∑ i y i log y ^ i H(y, \hat{y})=-\sum_{i} y_{i} \log \hat{y}_{i} H(y,y^)=−i∑yilogy^i 交叉熵是大于等于熵的,因为我们使用了带有预测误差的分布会带来更多bit的使用。(这里即使是预测的分布,也是严格遵守概率和为1的,只要有这个条件约束,预测分布求出来的熵就一定不会更小,只会大于等于。当 y y y和 y ^ \hat y y^相等的时候,交叉熵就等于熵了。)
KL散度
KL散度与交叉熵差别不大,公式如下:
K L ( y ∥ y ^ ) = ∑ i y i log 1 y ^ i − ∑ i y i log 1 y i = ∑ i y i log y i y ^ i K L(y \| \hat{y})=\sum_{i} y_{i} \log \frac{1}{\hat{y}_{i}}-\sum_{i} y_{i} \log \frac{1}{y_{i}}=\sum_{i} y_{i} \log \frac{y_{i}}{\hat{y}_{i}} KL(y∥y^)=i∑yilogy^i1−i∑yilogyi1=i∑yilogy^iyi其实不用看最后的推导结果,中间那个步骤是最好理解的,就是交叉熵减去真实分布解出的熵,其实就是表示预测误差带来了多少额外bit的使用。
当训练数据集定了后,真实分布求解出来的熵是个常数,可以忽略。所以,此时,最小化交叉熵和最小化KL散度得到的结果等价。
极大似然估计
知识的难以理解晦涩的中文翻译要背一半的锅,非要整些看起来就花里胡哨的名次让人摸不着头脑。就如同正则化,如果直译“regularization”这个词其实就是规则化嘛,这即使没看其中的数学原理,第一眼也大概知道是提前设置了一个规则去约束变量。极大似然估计也是一样的,“极大”就是“最大”,“似然”是对“likelihood”的一种近似文言文的翻译,说成大白话就是“可能性”,再直白点就是“像”。所以“极大似然估计”就是“它最像什么”。
求概率需要直到数据集的分布以及这个分布具体的参数,例如你知道数据符合均值0方差1的高斯分布,这样对于任意x,都能给出它出现的概率,极大似然估计正好相反。
极大似然估计是在已知一堆数据和分布类型的前提下,反推最有可能的参数是什么,也就是“它最像这个分布哪组参数下表现出来的数据”。例如一次考试过后你知道了全班的分数,你也直到考试分数这件事符合高斯分布,那么你就可以用极大似然估计来计算这次考试分数到底是符合均值多少方差多少的高斯分布。这里可能会提出一个问题,你咋就提前知道考试符合高斯分布了呢?
数据集的分布其实一半由数据集具体的业务背景得到,例如考试这件事多年经验就是大多数人都是中等成绩,极好极差的都是少数。如果从业务背景角度得不到,那就得依靠假设了。就是假设这个数据符合这个分布,然后当作已知条件用就可以,至于是不是真符合,那就不是我们工程师关心的问题了,这是数据科学家关注的点,我们一般只看结果是不是work的。其实机器学习算法中是有很多假设的,例如线性回归其实前提是假设数据符合高斯分布,逻辑回归假设数据符合伯努利分布,softmax假设数据符合多项分布。
接下来说一下似然函数。上面已经说过,极大似然估计是已知数据和分布类型了,未知的是参数,那么我们就把未知参数设为 θ \theta θ,那么已知数据的概率可以表示为:
∏ x P ( x ∣ θ ) \prod_{x}P(x|\theta) x∏P(x∣θ)连乘表示所有数据的概率。极大似然估计就是要求出使这个概率最大的参数 θ \theta θ,因为此 θ \theta θ下此分布下是最有可能产生长这个样子的数据的。
借用我参考的博客中的一个例子。假设有一个造币厂生产某种硬币,现在我们拿到了一枚这种硬币,想试试这硬币是不是均匀的。即想知道抛这枚硬币,正反面出现的概率(记为 θ \theta θ)各是多少?
于是我们拿这枚硬币抛了10次,得到的数据(x)是:反正正正正反正正正反。我们想求的正面概率 θ \theta θ是模型参数,而抛硬币模型我们可以假设是二项分布。
那么,出现实验结果x(即反正正正正反正正正反)的似然函数是多少呢?
f ( x , θ ) = ( 1 − θ ) × θ × θ × θ × θ × ( 1 − θ ) × θ × θ × θ × ( 1 − θ ) = θ 7 ( 1 − θ ) 3 = f ( θ ) f\left(x, \theta\right)=(1-\theta) \times \theta \times \theta \times \theta \times \theta \times(1-\theta) \times \theta \times \theta \times \theta \times(1-\theta)=\theta^{7}(1-\theta)^{3}=f(\theta) f(x,θ)=(1−θ)×θ×θ×θ×θ×(1−θ)×θ×θ×θ×(1−θ)=θ7(1−θ)3=f(θ)这是个只关于 θ \theta θ的函数。而最大似然估计,就是要最大化这个函数。我们可以画出 f ( θ ) f(\theta) f(θ)的图像:
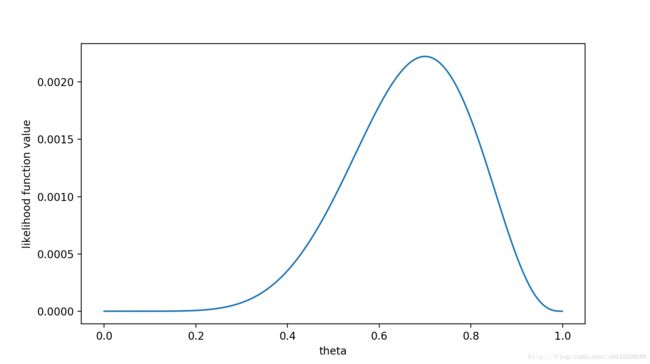
可以看出,在 θ = 0.7 \theta=0.7 θ=0.7时,似然函数取得最大值。
这样,我们已经完成了对 θ \theta θ的最大似然估计。即,抛10次硬币,发现7次硬币正面向上,最大似然估计认为正面向上的概率是0.7。(ummm…这非常直观合理,对吧?)
且慢,一些人可能会说,硬币一般都是均匀的啊! 就算你做实验发现结果是“反正正正正反正正正反”,我也不信 θ = 0.7 \theta=0.7 θ=0.7。
这里就包含了贝叶斯学派的思想了——要考虑先验概率。 为此,引入了最大后验概率估计。
最大后验概率估计
什么是先验概率?先验概率就是根据先前经验得到的概率,例如硬币正反面0.5这个事儿,就是根据先前经验得到的,已经作为一个知识深植在我们脑海了,所以也叫先验知识。
最大后验概率估计则是想求 θ \theta θ使 P ( x ∣ θ ) P ( θ ) P(x|θ)P(θ) P(x∣θ)P(θ)最大。求得的 θ θ θ不单单让似然函数大, θ θ θ自己出现的先验概率也得大。
MAP其实是在最大化 P ( θ ∣ x 0 ) = P ( x 0 ∣ θ ) P ( θ ) P ( x 0 ) P\left(\theta | x_{0}\right)=\frac{P\left(x_{0} | \theta\right) P(\theta)}{P\left(x_{0}\right)} P(θ∣x0)=P(x0)P(x0∣θ)P(θ),不过因为 x x x是确定的(即投出的“反正正正正反正正正反”), P ( x ) P(x) P(x)是一个已知值,所以去掉了分母 P ( x ) P(x) P(x)(假设“投10次硬币”是一次实验,实验做了1000次,“反正正正正反正正正反”出现了n次,则 P ( x ) = n / 1000 P(x)=n/1000 P(x)=n/1000。总之,这是一个可以由数据集得到的值。最大化 P ( θ ∣ x ) P(θ|x) P(θ∣x)的意义也很明确,即 x x x已经出现了,要求 θ θ θ取什么值使 P ( θ ∣ x ) P(θ|x) P(θ∣x)最大。顺带一提, P ( θ ∣ x ) P(θ|x) P(θ∣x)即后验概率,这就是“最大后验概率估计”名字的由来。
对于投硬币的例子来看,我们认为(”先验地知道“) θ θ θ取0.5的概率很大,取其他值的概率小一些。我们用一个高斯分布来具体描述我们掌握的这个先验知识,例如假设 P ( θ ) P(θ) P(θ)为均值0.5,方差0.1的高斯函数,如下图:
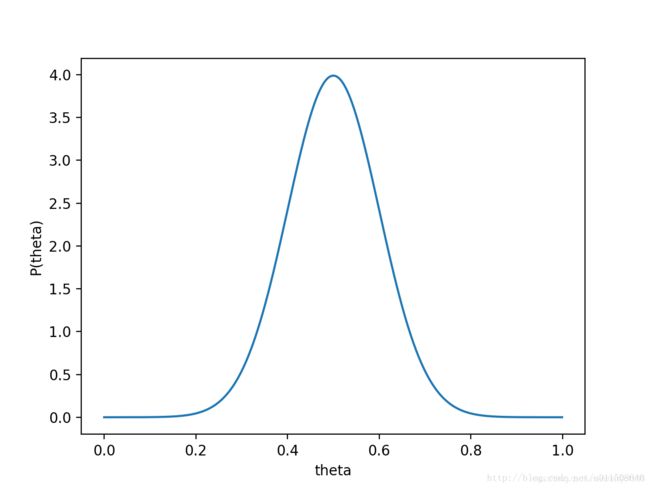
则 P ( x ∣ θ ) P ( θ ) P(x|θ)P(θ) P(x∣θ)P(θ)的函数图像为:
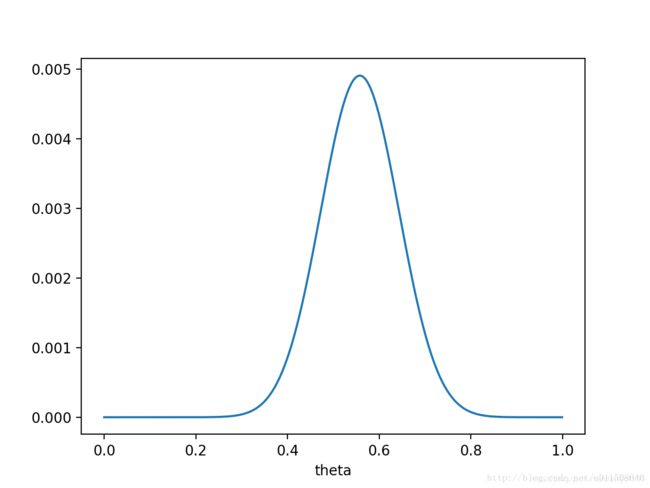
注意,此时函数取最大值时, θ θ θ取值已向左偏移,不再是0.7。实际上,在 θ = 0.558 θ=0.558 θ=0.558时函数取得了最大值。即,用最大后验概率估计,得到 θ = 0.558 θ=0.558 θ=0.558
最后,那要怎样才能说服一个贝叶斯派相信θ=0.7呢?你得多做点实验…
如果做了1000次实验,其中700次都是正面向上,这时似然函数为:
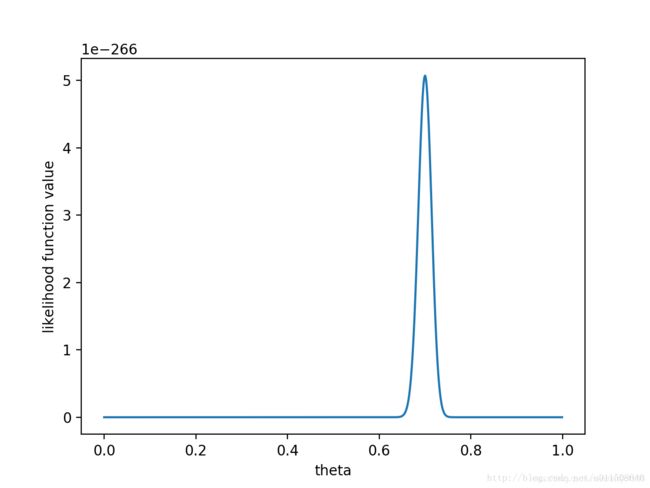
如果仍然假设 P ( θ ) P(θ) P(θ)为均值0.5,方差0.1的高斯函数, P ( x ∣ θ ) P ( θ ) P(x|θ)P(θ) P(x∣θ)P(θ)的函数图像为:
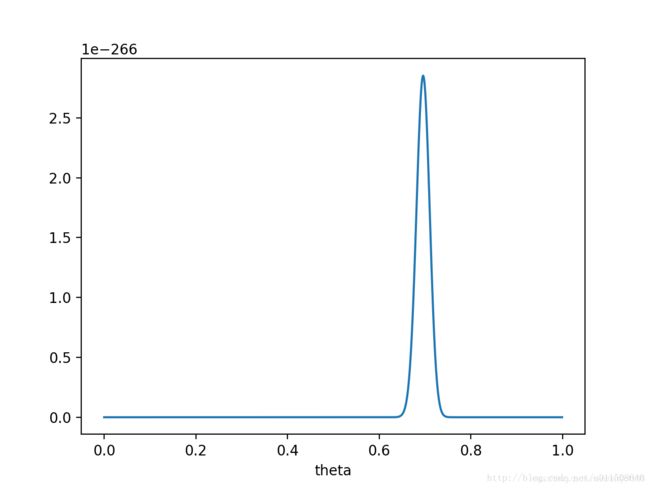
在 θ = 0.696 θ=0.696 θ=0.696处, P ( x ∣ θ ) P ( θ ) P(x|θ)P(θ) P(x∣θ)P(θ)取得最大值。
这样,就算一个考虑了先验概率的贝叶斯派,也不得不承认得把 θ θ θ估计在0.7附近了。
PS. 要是遇上了顽固的贝叶斯派,认为 P ( θ = 0.5 ) = 1 P(θ=0.5)=1 P(θ=0.5)=1,那就没得玩了。。(这里原作者的意思是 θ \theta θ取0.5的概率为1,取其他都为0,这样画出来的图中就只有取0.5处有值了) 无论怎么做实验,使用MAP估计出来都是 θ = 0.5 θ=0.5 θ=0.5。这也说明,一个合理的先验概率假设是很重要的。(通常,先验概率能从数据中直接分析得到)
最大后验概率估计就是在极大似然估计后面加了个先验概率,或者说极大似然估计将先验概率认为是均匀分布,即每一处概率都是相等的,这样就相当于后面乘了个常数,等于没有。
正则化也是一种先验概率,L1正则化相当于拉普拉斯鲜艳,L2正则化相当于高斯先验。为啥正则化是加在后面而不是乘?其是一样的,极大似然估计求解时加个log,也就成累加了。
四者的关系
上面只说了KL散度和交叉熵的关系,以及极大似然估计和最大后验概率估计的关系,其实交叉熵和极大似然估计也是有关系的。
扩展到多分类问题,极大似然估计假设数据符合多项分布,假设有n个类别,那么似然函数为:
f ( x ∣ θ ) = P ( x = c , w ) f(x|\theta)=P(x=c, w) f(x∣θ)=P(x=c,w)其中c为真实标签。上面说了引申到多分类,那么将n个类别都引进来就会得到:
f ( x ∣ θ ) = ∏ c = 1 n P ( x = c , w ) y c f(x|\theta)=\prod_{c=1}^{n} P(x=c, w)^{y_{c}} f(x∣θ)=c=1∏nP(x=c,w)yc上式仍然表示一个样本的似然,即使它有累乘操作。 y c y_c yc表示标签。当c为这个样本真实标签时, y c = 1 y_c=1 yc=1,否则为0。所以其实本质没变。
同样的,对于m个样本,写出其对数似然,再加个对数变换:
ln L ( w ∣ X ) = ∑ i = 1 m [ ∑ c = 1 n y i c ln P ( x i = c , w ) ] \ln L(w | X)=\sum_{i=1}^{m}\left[ \sum_{c=1}^{n} y_{ic} \ln P(x_i=c, w)\right] lnL(w∣X)=i=1∑m[c=1∑nyiclnP(xi=c,w)]差个负号就是交叉熵了,极大化似然,相当于极小化负的似然,就是交叉熵了。
总结一下: KL散度与交叉熵差了个值为常数的真实分布的熵,交叉熵与极大似然估计等价,所以,极小化KL散度、极小化交叉熵、极大化似然得到的结果等价。极大似然估计与最大后验概率估计差了个先验,类似正则化。