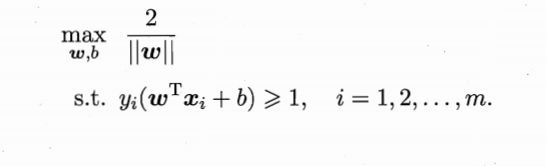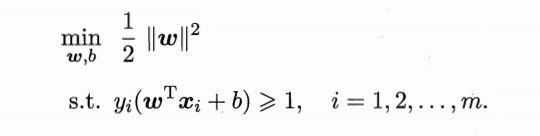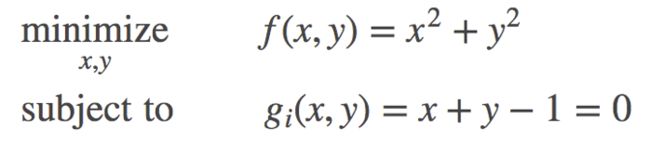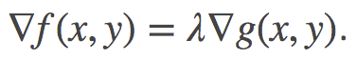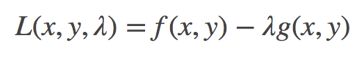拉格朗日乘子法求解最优化问题

 

     最近在看机器学习有关SVM的内容，在SVM模型中，我们要求得一个划分超平面，使得相同类别的样本处于同一边，不同类别的样本分开。我们想要找到具有“最大间隔”的划分超平面，即满足以下约束的平面：

求解上式等价于求解：

求解以上带不等式约束的最小值问题，即可获得最优划分超平面。至此引入我们这篇文章讲述的主要内容：“使用拉格朗日乘子法求解最优化问题”，下面我们先从最简单的最优化问题一步步开始讲述。

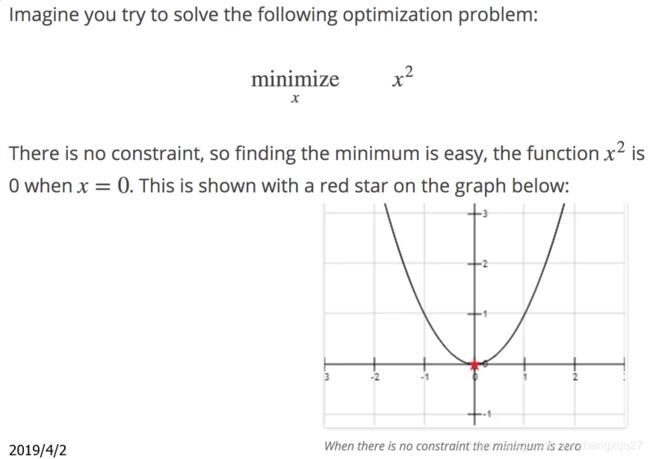
    (1）无约束条件的最优化问题

     【例1】

       这是最为简单的情况，通常情况我们只需要对变量求导数，令导函数等于0即可获得极值点的位置，再从极值点中找出最值即可。

   (2）带等式约束的最优化问题

   【例2】

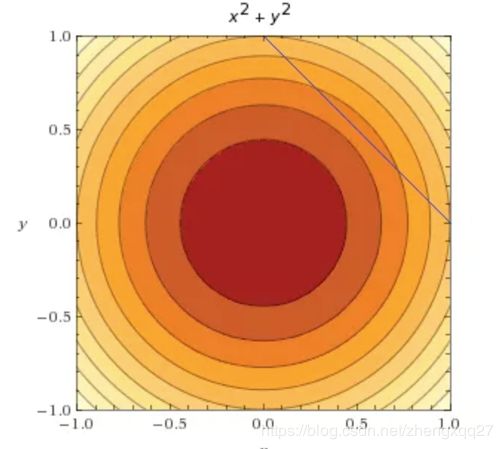
     对于这个例子，我们首先使用等高线图来直观地表示目标函数和约束函数，如下图所示：

    观察以上的等高线图，有以下两点注意：

         1、颜色越深的地方的值越小；

         2、同一条等高线上的函数取值相同；

    我们把上面两幅图结合到一起，由于我们只关心g(x,y）= 0 的情况，所以我们只画出x+y-1 = 0的线( 直线x+y-1 = 0也叫作可行域(feasible set) )，如下所示：

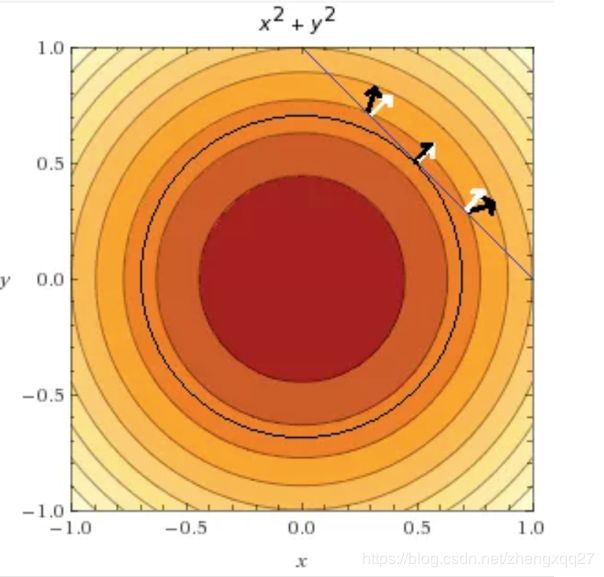
   好，那么我们究竟要如何求解上述问题的最优解呢？仔细观察上图，你能不能发现，在约束条件g(x,y) = 0 的条件下，f(x,y)取得最小值的情况是函数 f(x,y) 和函数 g(x,y) 的梯度平行！或许你还不太明白这是什么意思，那请看下面的图：

由上图，可以清楚地看到，当函数 f(x,y) 和函数 g(x,y) 的梯度平行时，函数 f(x,y)取得最小值。到这里我们知道了取得最优解的条件，那么要如何数学化地表示出来呢？请看下面的公式：

上面公式中的λ叫做拉格朗日乘子 ，代表着上述式子取得最优解时并不一定要两个函数的梯度相同，只要平行即可。

 注意，上面的式子等价于：

为求解该最优化问题，我们定义函数 L(x,y,λ) 如下：

其梯度为：

函数L(x,y,λ)具有以下性质：

    1、当x,y均相同时，函数L(x,y,λ)的值等于函数f(x,y)的值（因为减掉的λg(x,y)的值始终为0）；

    2、函数L(x,y,λ)的导函数为0的点，即为函数f(x,y)的极值点(根据以上分析可得)；

由上，例2的求解方法如下：

所以，求解带等式约束条件的最优解问题，可通过构造对应的拉格朗日函数求解。

(3）带等式约束与不等式约束的最优化问题

对于带等式约束与不等式约束的最优化问题，我们先写出其一般形式：

由（2），我们仍然可以通过令其各变量的偏导数为0来求解最优解，但是这样或许并不是一个很好的解决方案，原因如下：

     1、参数α和β总共k+l个，如果全部求偏导工作量太大，不现实；

     2、此问题可能根本没有最优解；

针对上述情况，我们对问题换一种思路思考，利用对偶的思想，将原问题转化为其对偶问题进行求解。有关对偶问题的讲解将在我的其他博客再行详解讨论，欢迎大家关注我的博客。

---

谢谢阅读！